 E2, ∥f(x) - f(y)∥ = ∥x - y∥.
E2, ∥f(x) - f(y)∥ = ∥x - y∥.
a) On suppose que E = F = R. Montrer que f est linéaire.
b) On suppose que E = F et que la norme est euclidienne. Montrer que f est linéaire.
c) On suppose que f est surjective. Montrer que f est linéaire.
d) Donner un exemple dans lequel f n’est pas linéaire.
Solution de Ivan Gozard
Notons qu’une fonction vérifiant l’hypothèse est lipschitzienne, donc continue, et en outre injective.
a) Dans le cas où E = F = R, f est strictement monotone Quitte à changer f en - f, on
peut la supposer strictement croissante et alors, si x > y, f(x) - f(y) = x - y. Donc
x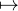 f(x) - x est constante, et cette constante vaut 0 puisque f(0) = 0. Finalement,
f = ± Id R .
f(x) - x est constante, et cette constante vaut 0 puisque f(0) = 0. Finalement,
f = ± Id R .
b) Notons que ∥f(x)∥ = ∥x∥ pour tout x. Par élévation au carré, pour tout (x,y)  E2,
E2,
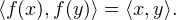
Il en résulte que, si a et b sont dans R, pour tout (x,y,z)  E3,
E3,
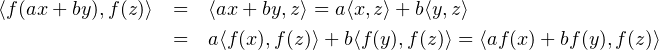
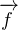 (E). Comme
f(ax + by) - af(x) - bf(y) appartient à
(E). Comme
f(ax + by) - af(x) - bf(y) appartient à 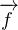 (E), f(ax + by) - af(x) - bf(y) = 0 et f est
linéaire.
c) ∙ On note G(E,F) l’ensemble des isométries bijectives de E sur F . Si g
(E), f(ax + by) - af(x) - bf(y) = 0 et f est
linéaire.
c) ∙ On note G(E,F) l’ensemble des isométries bijectives de E sur F . Si g  G(E,F), alors
g-1
G(E,F), alors
g-1  G(F, E) et, si h
G(F, E) et, si h  G(F,F), g-1hg
G(F,F), g-1hg  G(E,E). Nous allons montrer que, si g
G(E,E). Nous allons montrer que, si g  G(E,F), g
conserve le milieu.
G(E,F), g
conserve le milieu.
Fixons donc (x, y)  E2. Posons r :=
E2. Posons r := 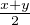 et, pour h appartenant à G(E,F) ou G(E,E),
et, pour h appartenant à G(E,F) ou G(E,E),
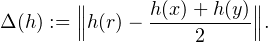
On a évidemment
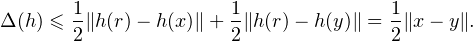
Fixons g  G(E, F). Posons ω :=
G(E, F). Posons ω := 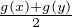 et notons s
et notons s  G(F,F) la symétrie centrale par
rapport à ω. Elle intervertit g(x) et g(y). Nous allons comparer Δ(g-1sg) à Δ(g). On
a
G(F,F) la symétrie centrale par
rapport à ω. Elle intervertit g(x) et g(y). Nous allons comparer Δ(g-1sg) à Δ(g). On
a
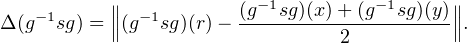
On a (g-1 sg)(x) = g-1(g(y)) = y et de même (g-1sg)(y) = x. En outre, pour tout t, t + s(t) = 2ω, donc s(t) = 2ω - t = g(x) + g(y) - t et donc s(g(r)) = g(x) + g(y) - g(r). Finalement,
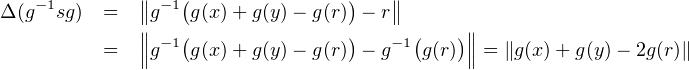
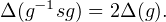
Posons h := g-1 sg  G(E,E). En appliquant ce qui précède à E = F , on obtient, en notant σ la
symétrie centrale par rapport à
G(E,E). En appliquant ce qui précède à E = F , on obtient, en notant σ la
symétrie centrale par rapport à 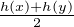 , que
, que
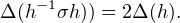
Puisque Δ G(E,E)
G(E,E)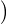 est borné, il est réduit à 0. Donc Δ(h) = 0 et Δ(g) = 0 par conséquent.
Ainsi, g conserve le milieu.
est borné, il est réduit à 0. Donc Δ(h) = 0 et Δ(g) = 0 par conséquent.
Ainsi, g conserve le milieu.
∙ En prenant y = 0, on obtient que g(x) = 2g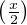 . Puis
. Puis
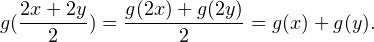
 g(tx), de R vers E, est additive et continue, et il est bien connu que
ceci entraîne sa linéairité. Donc g(λx) = λg(x) et g est bien linéaire.
g(tx), de R vers E, est additive et continue, et il est bien connu que
ceci entraîne sa linéairité. Donc g(λx) = λg(x) et g est bien linéaire.
d) On munit R 2 de la norme définie par ∥(x,y)∥∞ := max(|x|,|y|). Considérons la fonction
t (t, sin t), de R vers R2. On a
(t, sin t), de R vers R2. On a
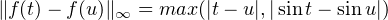
Le résultat établi dans la question c est connu sous le nom de théorème de Mazur-Ulam. Il a déjà fait l’objet d’un exercice dans notre revue : ex. 49, pp. 62-64, vol. 121, n•4, juin 2011.

