88. Soient n N^*, f une application continue de Rⁿ dans R telle que, pour tout (x,y) de Rⁿ× R ⁿ , t [0, 1]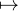f((1 - t)x + ty) est monotone. Montrer qu’il existe une forme linéaire φ sur R ⁿ et une application continue monotone g de R dans R telles que f = g • φ.

On munit E = R ⁿ de sa structure euclidienne canonique. Nous utiliserons la :

Démonstration. Choisissons ω E \ C et considérons p l’unique point de C tel que

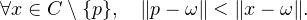
Posons F := {x E∣⟨x - p∣ω - p⟩≤ 0} ; il est classique que F est un demi-espace fermé contenant C.

Soit m 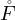= {x E∣⟨x - p∣ω - p⟩ < 0} ; on a p [m,2p - m]. Comme p C et 2p - m E \ F ⊂ E \C, on a, par convexité de E \C, m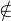E \C, donc m C. Ainsi 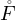⊂ C, et donc F, qui est l’adhérence de 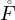est inclus dans C. Par conséquent, F = C et C est bien un demi-espace fermé. __

Prouvons maintenant le résultat demandé. On peut supposer f non constante, de sorte que, dans R, inff < sup f.

Pour λ ] inf f, supf[, soit F_λ := {x E∣f(x) ≤ λ}. Alors, F_λ est fermé, distinct de ∅ et de E. La propriété de monotonie de f montre que F_λ et E \ F_λ sont convexes. Par conséquent F_λ est un demi-espace fermé et on dispose de (u_λ,a_λ) E × R tel que ∥u_λ∥ = 1 et F_λ = {x E∣ ⟨u_λ∣x⟩≤ a_λ}.

Si λ ≤ μ, on a F_λ ⊂ F_μ, donc u_λ = u_μ et a_λ ≤ a_μ. L’application λ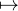u_λ est donc constante sur ] inf f, sup f[, et si on note v sa valeur, on a

Soient x et y dans E tels que f(x) < f(y) et soit λ . On a

d’où ⟨v∣ x⟩ < ⟨v∣ y⟩. Ainsi, pour x,y E,

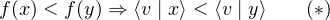
On en déduit que, pour x,y E,

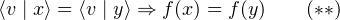
Soit g : R → R , t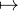f(tv) ; par composition, g est continue. Pour x E,

donc f(x) = f(⟨x∣v⟩v) = g(⟨x∣v⟩).

Enfin, pour t < tʹ, ⟨tv∣v⟩ < ⟨tʹv∣v⟩, donc, selon (*), f(tv) ≤ f(tʹv), soit g(t) ≤ g(tʹ), ce qui montre que g est croissante.

Posons ϕ : E → R, x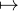⟨v∣x⟩. On a f = g • ϕ où ϕ est une forme linéaire et g : R → R est croissante et continue.

[Liste des corrigés]