a) Montrer que φ est continue.
b) On note Eφ l’ensemble des fonctions f : R → R continues par morceaux telles que φ•|f|
soit intégrable sur R. Montrer que Eφ est un sous-espace vectoriel de RR si et seulement s’il
existe C > 0 tel que : ∀x  R+*, φ(2x) ≤ Cφ(x).
R+*, φ(2x) ≤ Cφ(x).
a) Toute fonction convexe sur R+ est continue sur R+*. La continuité en 0 découle
par exemple de l’encadrement 0 ≤ φ(x) ≤ xφ(1) + (1 - x)φ(0) = xφ(1) pour tout
x  [0, 1].
[0, 1].
b) Observons tout d’abord que φ est croissante, en effet le taux d’accroissement
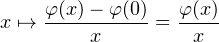
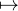 φ(x) = x.
φ(x) = x.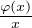 l’est aussi.
l’est aussi.
∙ Supposons qu’il existe C > 0 tel que φ(2x) ≤ Cφ(x) pour tout x > 0. Il en résulte que, pour tous x, y ≥ 0, on a
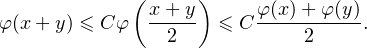
 Eφ, alors on
a
Eφ, alors on
a
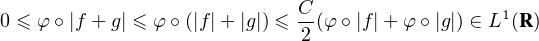
 Eφ. Soit λ
Eφ. Soit λ  R et f
R et f  Eφ. On prend un entier
n > 0 tel que 2n ≥|λ|. Alors on a φ •|λf|≤ φ • (2n|f|) ≤ Cnφ •|f|
Eφ. On prend un entier
n > 0 tel que 2n ≥|λ|. Alors on a φ •|λf|≤ φ • (2n|f|) ≤ Cnφ •|f| L1(R), donc
λf
L1(R), donc
λf  Eφ .
Eφ .
∙ Supposons que Eφ soit un sous-espace vectoriel de RR. Le cas où φ est la fonction
nulle étant trivial, on peut supposer qu’il existe x > 0 tel que φ(x) > 0. Comme φ est
croissante et continue, il existe A ≥ 0 tel que φ = 0 sur [0,A] et φ > 0 sur ]A,+∞[. Par
l’absurde si A > 0, alors la fonction constante f = A est dans Eφ (puisque φ • f = 0)
tandis que 2f Eφ (puisque φ • (2f) est constante > 0 sur R). Ainsi on a φ > 0 sur
R+*.
Eφ (puisque φ • (2f) est constante > 0 sur R). Ainsi on a φ > 0 sur
R+*.
Montrons le résultat souhaité par l’absurde, ce qui revient à supposer l’existence d’une suite
(an )n≥1 dans R +* telle que φ(2an) > nφ(an) pour tout n  N*. On considère alors une fonction
en escalier f dont le graphe est formé de rectangles de hauteur an et de largeur bn = (n2φ(an))-1.
Plus précisément, soit (xn) une suite croissant vers + ∞ suffisamment vite de sorte que
xn+1 > xn + bn pour tout n ; on définit f par
N*. On considère alors une fonction
en escalier f dont le graphe est formé de rectangles de hauteur an et de largeur bn = (n2φ(an))-1.
Plus précisément, soit (xn) une suite croissant vers + ∞ suffisamment vite de sorte que
xn+1 > xn + bn pour tout n ; on définit f par
.
n∈N*](/numeros/RMS130-3/RMS130-3778x.png)
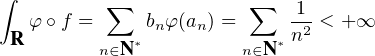
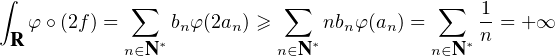
 Eφ et 2f
Eφ et 2f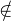 Eφ. Cette contradiction conclut le raisonnement.
Eφ. Cette contradiction conclut le raisonnement.
[Liste des corrigés]

