80. a) Montrer que l’on ne peut partitionner R² en cercles de rayons strictement positifs.

b) Peut-on partitionner R² en disques ouverts de rayons strictement positifs ?

c) On appelle triade toute partie de R² homéomorphe à la réunion des trois segments reliant le point (0, 0) aux points (0,1), (1,0) et (1,1). Montrer que l’on ne peut partitionner R² en triades.

a) Supposons qu’il existe une telle partition. Soit C₀ = C(A₀,R₀) (où C(A,R) désigne le cercle de centre A et de rayon R > 0) l’un de ces cercles puis, par récurrence, C_n+1 = C(A_n+1,R_n+1) le cercle de la partition passant par A_n. On a clairement R_n+1 < 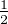R_n et, puisque les points A_k pour k ≥ n sont dans l’intérieur du cercle C_n,

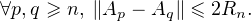
Ainsi, la suite (A_n)_n est de Cauchy et par conséquent convergente. Soit A sa limite et R > 0 le rayon du cercle C passant par A. À nouveau parce que la suite (A_k)_k≥n est contenue dans l’intérieur de C_n , A appartient à chaque disque fermé délimité par C_n, lequel contient donc C. Il vient R ≤ R_n pour tout n, donc R = 0, ce qui est absurde.

b) La réponse est négative. Soit en effet (U_i)_iI une partition de R² en parties ouvertes (et non vides par définition même d’une partition). Étant donné i₀ I, U_i0 et ⋃ _iI\{i0}U_i forment une partition de R ² en deux ouverts. Par connexité par arcs de R², U_i0 = R² et I \{i₀} = ∅. La seule partition de R ² en ouverts est donc {R²}.

c) On va dans un premier temps montrer qu’il n’existe pas de partition au plus dénombrable de R² en triades, puis établir un lemme technique pour, finalement, montrer qu’une famille de triades deux à deux disjointes est au plus dénombrable.

Nous utiliserons deux théorèmes hors programme dont nous rappelons l’énoncé sans démonstration. Le théorème de Baire, assez facile à démontrer, et le théorème de Jordan qui est nettement plus difficile mais dont l’énoncé est très intuitif :

Première étape

Commençons par établir le

Preuve. Soit f : [0,1] → R² continue et injective. Par compacité de [0,1], f induit un homéomorphisme de [0,1] dans f([0,1]). Si f([0,1]) contient une boule ouverte B, alors J = f^-1 (B) est une partie ouverte et connexe par arcs de [0,1], donc un intervalle non trivial. Soit t₀ un élément intérieur à J. L’application f induit un homéomorphisme de J \{t₀} sur B \ {f(t₀ )}. C’est absurde car B \{f(t₀)} est connexe par arcs tandis que J \{t₀} ne l’est pas.

On déduit immédiatement de ce lemme qu’une triade est d’intérieur vide.

Soit alors (T_i )_iI une famille au plus dénombrable de triades. Comme T_i est compact (puisqu’homéomorphe à une réunion de trois segments), c’est un fermé d’intérieur vide de R² et, d’après le théorème de Baire, ⋃ _iIT_i est d’intérieur vide. Ainsi il n’existe pas de partition de R² en une famille au plus dénombrable de triades.

Seconde étape

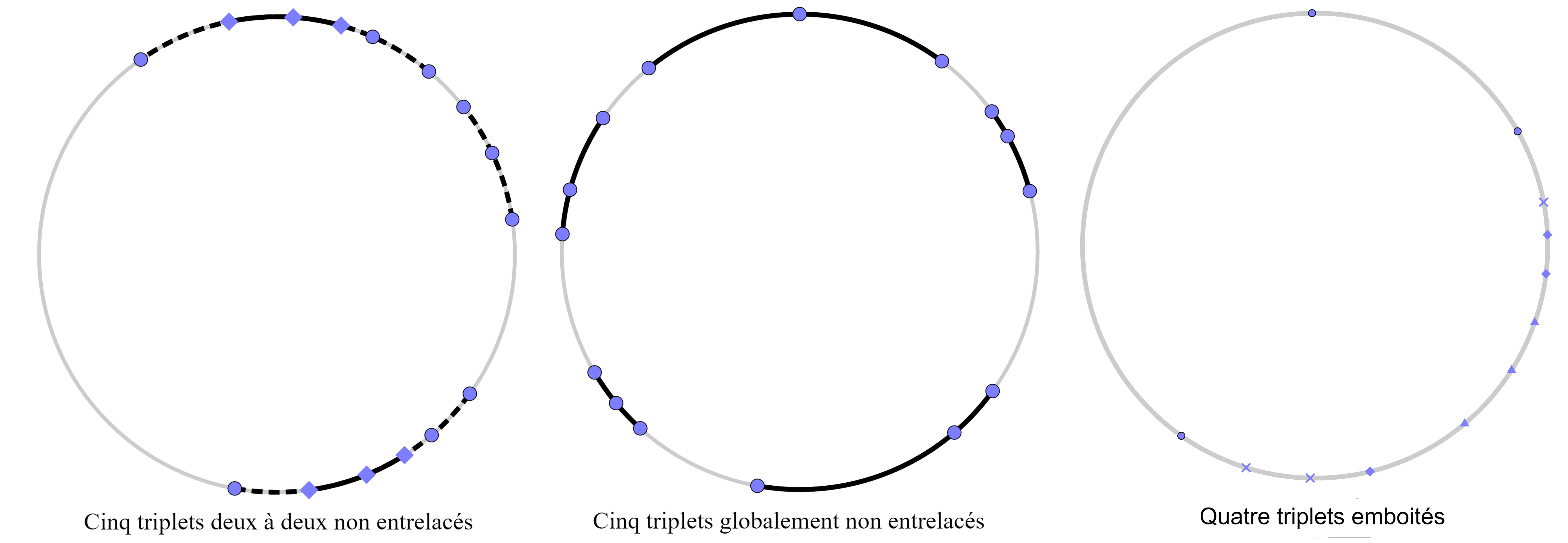
On montre ici un lemme technique qui sera mis en oeuvre dans la troisième étape. Soit C le cercle unité de R ² et U, V deux triplets de C. On dira qu’ils sont non entrelacés, si chacun est contenu dans l’un des arcs ouverts de C délimités par l’autre. Et, étant donnée (U_i)_I une famille de triplets de C, on dira qu’elle est globalement non entrelacée si pour chaque i I, l’un des trois arcs de C délimités par U_i contient tous les U_j pour j ⁄= i. Nous dirons enfin qu’une suite (U_k)_kN de triplets de C est emboîtée si pour chaque k N, l’un des arcs délimités par U_k contient tous les U_l pour l > k.

Avec ces définitions, nous avons le

Preuve. Soit (U_i )_iI une famille infinie de triplets de C. Supposons qu’on ne puisse en extraire une suite emboîtée et montrons qu’il existe une suite (i_k)_kN^* I^N* telle que (U_ik)_k soit globalement non entrelacée.

Fixons i₁ I. Chacun des U_i, i ⁄= i₁, est contenu dans l’un des trois arcs ouverts de C délimités par U_i1 . L’un d’entre eux contient une infinité des U_i, disons tous les U_i pour i I₁ où I₁ est une partie infinie de I. Notons A₁ son complémentaire (donc l’adhérence de la réunion des deux autres arcs).

Supposons maintenant choisis i₁,…,i_p I deux à deux distincts et une partie infinie I_p ⊂ I \ {i₁ , … , i_p} tels que :

• Les triplets U_i1, U_i2,…, U_ip sont globalement non entrelacés : on notera A_k la réunion de deux des arcs fermés de C définis par U_ik dont le complémentaire contient tous les U_il , l [[1,p]] \{k}.
• Chaque triplet U_j pour j I_p est contenu dans C \⋃ _1≤k≤pA_k.

et démontrons qu’il est loisible de choisir i_p+1 et I_p+1 en conservant ces propriétés. Choisissons j₀ I_p . Par hypothèse, U_j0 est contenu dans l’un des p arcs ouverts qui composent C \ ⋃ _1≤k≤pA_k ; désignons par D₀ la réunion des deux arcs délimités par U_j0 et contenus dans cet arc.

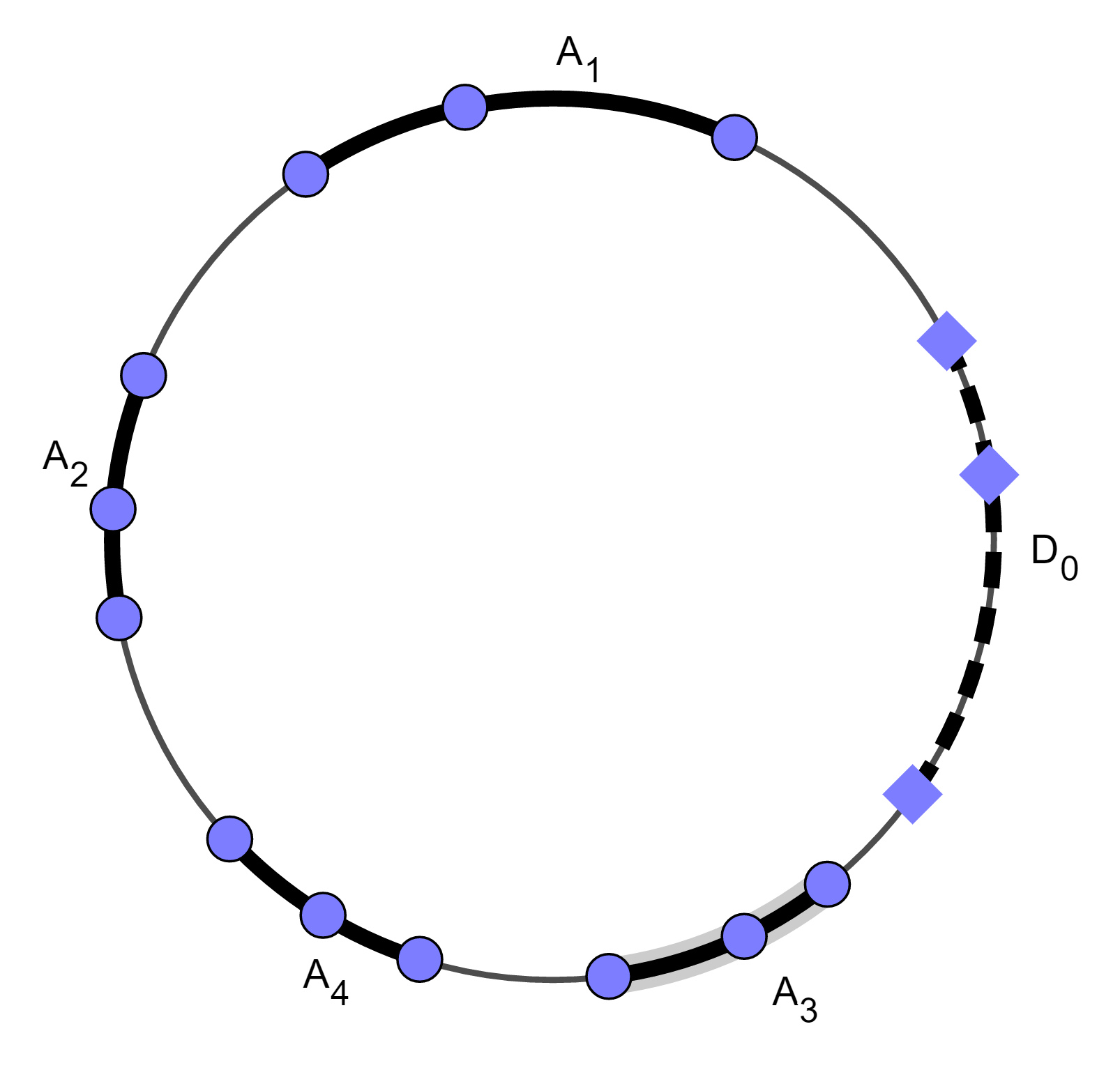
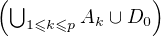S’il existe une infinité de j I_p tels que U_j soit contenu dans C \, on peut poser i_p+1 = j₀ et choisir I_p+1 en conséquence. Sinon, l’un des deux arcs de D₀ délimités par U_j0 contient une infinité des U_j, j I_p. Soit U_j1 l’un d’entre eux et D₁ la réunion des deux arcs délimités par U_j1 et contenus dans D₀.

Comme pour j₀ , s’il existe une infinité de j I_p tels que U_j soit contenu dans
C \ 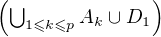, on peut poser i_p+1 = j₁ et choisir I_p+1 en conséquence.

Sinon l’un des deux arcs de D₁ délimités par U_j1 contient une infinité des U_j, j I_p, etc. Si à aucun moment on ne peut choisir i_p+1 = j_k, on obtient une suite emboîtée (U_jk). Comme une telle suite n’existe pas par hypothèse, on peut choisir i_p+1 et I_p+1 de manière convenable.

Troisième étape

On va établir qu’une famille de triades deux à deux disjointes est au plus dénombrable.

Pour une triade T, on appellera centre de T l’image du point (0,0) et extrémités de T les images des points (0,1), (1,0) et (1,1) (par un homéomorphisme dont fait état la définition d’une triade – on peut vérifier que ces définitions sont indépendantes du choix de l’homéomorphisme mais on peut s’en passer ici en appelant triade la donnée d’un tel homéomorphisme plutôt que sa seule image). Les images des trois segments seront appelés les brins de T.

Preuve. On appellera module d’une triade T , et on notera m(T), le minimum des distances du centre aux extrémités.

Soit une famille non dénombrable (Tʹ_j)_jJ de triades deux à deux disjointes. Comme J = ⋃ _nN^*{j J;m(T_j) ≥ 1⁄n} n’est pas dénombrable, il existe K ⊂ J non dénombrable et η > 0 tel que m(T_k) ≥ η pour tout k K. Quitte à faire une homothétie de rapport 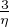, on peut supposer m(T_k ) ≥ 3. Il existe ensuite L ⊂ K non dénombrable tel que les centres des (T_l)_lL appartiennent à un disque ouvert de rayon 1 (car R² peut s’écrire comme réunion dénombrable de disques ouverts de rayon 1). Quitte à effectuer une translation, on peut supposer qu’il s’agit du disque unité centré en 0. Puisque m(T_l) ≥ 3, les extrémités de chaque T_l sont à l’extérieur du disque unité. On peut alors ne conserver de chaque brin de T_l que sa partie joignant le centre au premier point de rencontre avec C ; on notera encore T_l la triade obtenue après cette ≪amputation ≫  :

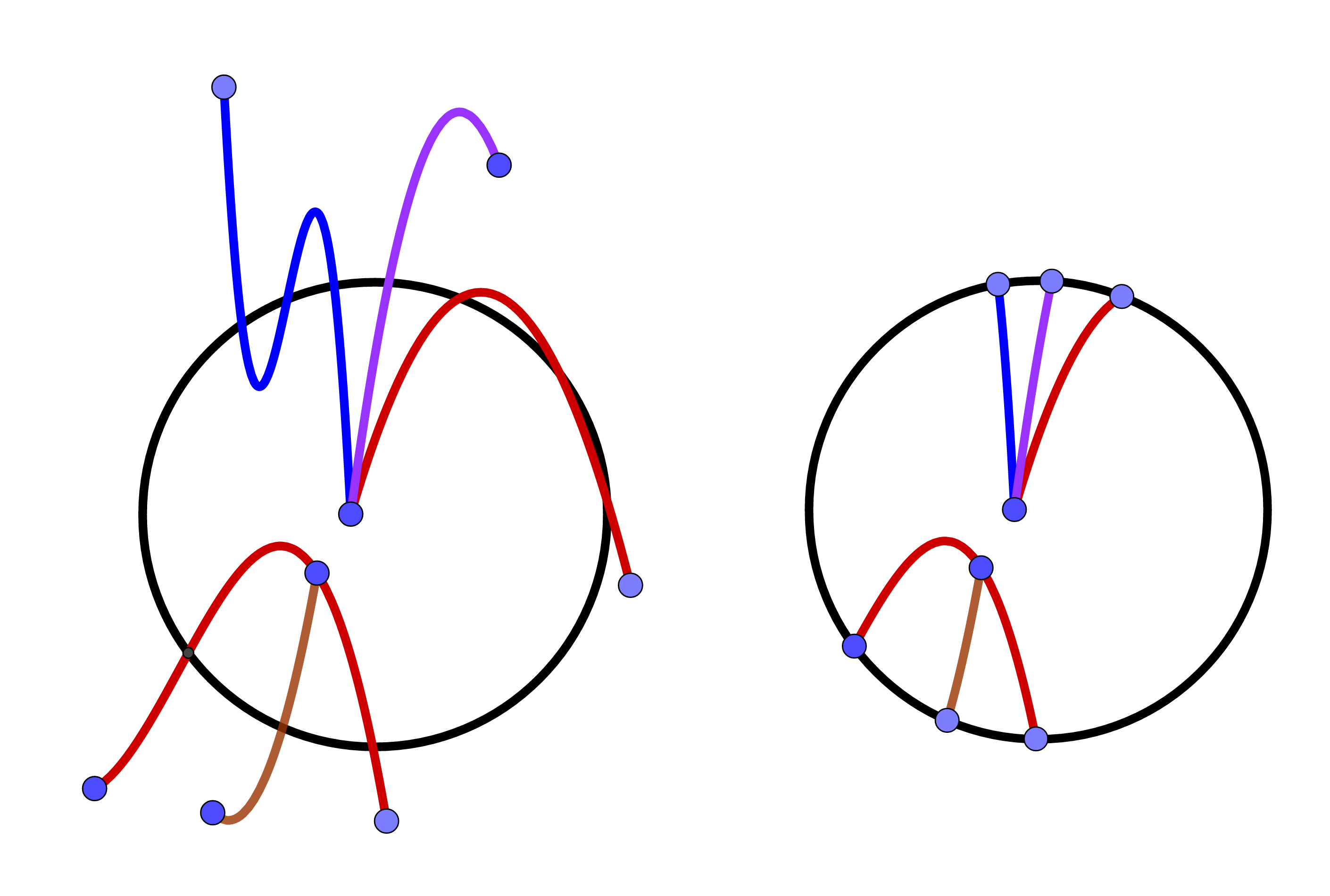
Enfin, en notant L(T_l) le minimum des longueurs des trois arcs de C délimités par les extrémités de T_l , il existe α > 0 et I ⊂ L infini tel que L(T_i) ≥ α pour tout i I (car sinon, L = ⋃ _nN^*{l J;L(T_l) ≥ 1⁄n} serait dénombrable) : la famille (T_i)_iI satisfait aux conditions du lemme 3.

Supposons donc l’existence d’une famille (T_i)_iI de triades telle que décrite par le lemme 3. Par le théorème de Jordan, les trois brins de T_i ainsi que C délimitent trois parties connexes par arcs du disque défini par C et toute autre triade de la famille est contenue dans l’une de ces parties. En conséquence, si l’on note U_i le triplet de C formé par les extrémités de T_i, ces triplets sont deux à deux non entrelacés. D’après le lemme 2, on peut en extraire soit une suite emboîtée, soit une suite globalement non entrelacée. Dans les deux cas c’est absurde puisque les longueurs des arcs définis par les U_i sont toutes minorées par α.

[Liste des corrigés]