78. Soient E un R-espace vectoriel de dimension finie, v1,…,vp des vecteurs de E et C = R + v1 + ⋅⋅⋅ + R+vp. Montrer que C est fermé dans E.

Solution de Christophe Jan

On effectue une récurrence sur n = dim(E) ; soit 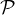P(n) la propriété :

≪si E est un R -espace de dimension égale à n, pour tous vecteurs v1,…,vp de E, alors C = R + ⋅ v1 + ⋅⋅⋅ + R+ ⋅ vp est fermé dans E. ≫

⊳ Lorsque n = 1, E est isomorphe à R. Soient v1,…,vp des vecteurs de R. On distingue plusieurs cas.

  • Tous les vk sont nuls. Alors, C = {0} qui est fermé.
  • Tous les vk sont de même signe et l’un est non nul. Par exemple, tous les vk sont négatifs ou nuls. Alors, chaque R+ ⋅ vk vaut {0} ou R- et C = R- qui est fermé.
  • Deux vecteurs vk sont de signes différents. Alors, C = R qui est fermé.

⊳ On suppose l’assertion vraie pour un certain entier n ∈ N*. Soit E un R-espace vectoriel de dimension (n + 1). On se donne des vecteurs v1,…,vp dans E. Si tous les vecteurs vk sont nuls, alors C = {0} qui est fermé. Sinon, l’un des vecteurs vk est non nul, par exemple le vecteur vp. Soit x ∈ C . On va exhiber une suite (xr)r∈N d’éléments de C convergeant vers x. 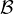On complète la famille libre (vp ) en une base B de E et on note f 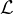∈L(E) la projection orthogonale sur F = v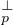⊥p parallèlement à R ⋅ vp, ainsi que g = idE - f : u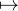↦→ < vp,u > ⋅vp la projection orthogonale sur R.vp .

L’hyperplan F est un R-espace de dimension n. On pose

D = f(C) = R + ⋅ f(v1) + ⋅⋅⋅ + R+ ⋅ f(vp-1),

car f(vp ) = 0 et f est linéaire. On pose y = f(x) et pour tout r ∈ N, yr = f(xr) ∈ D. On peut appliquer l’hypothèse de récurrence dans l’espace F : l’ensemble D est fermé, donc le vecteur y appartient à l’ensemble D. on peut écrire :

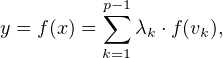
p∑-1 y = f(x) = λk ⋅f(vk), k=1
où les scalaires λk sont positifs ou nuls.

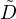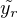D’autre part, on peut appliquer l’hypothèse d’initialisation à l’espace G = g(E) = V ect(vp). L’ensemble ˜D = g(C) = R+ ⋅g(v1) + ⋅⋅⋅ + R+ ⋅g(vp) est fermé. Pour tout r ∈ N, le vecteur xr est dans C, donc ˜yr = g(xr) est dans 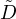˜D et la limite g(x) = limr→+∞g(xr) reste dans ˜D.

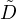On peut écrire :

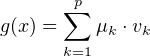
∑p g(x) = μk ⋅vk k=1
où les scalaires μk sont positifs ou nuls. En conclusion, le vecteur

x = f(x) + g(x) = 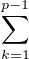p-1 ∑ k=1(λk + μk) ⋅ vk + μp ⋅ vp

est bien dans l’ensemble C ; l’ensemble C est bien fermé.

David Alexander mentionne que le résultat est connu comme le théorème de Farkas-Minkowski.
[Liste des corrigés]


[ < ]