61. Soit n ≥ 2 un entier.

a) Soient A et B dans Mn(C), L la matrice de Mn(n-1)2,n(C) dont les lignes sont les Ai Bj - Bj Ai , 1 ≤ i,j ≤ n - 1. Montrer que A et B ont un vecteur propre commun si et seulement si rg (L) < n.

b) Montrer que l’ensemble des A de Mn(C) tels que A et tA n’admettent aucun vecteur propre commun est un ouvert dense de Mn(C).

Solution de Mohamed Houkari

a) ∙ Supposons que A,B ont un vecteur propre commun X. On note λ (resp. μ) la valeur propre de A (resp. B) associée. Alors, pour tous i,j ∈ [[1;n - 1]], on a

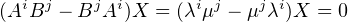
i j j i i j j i (A B - B A )X = (λ μ - μ λ )X = 0

donc X appartient au noyau de L, ce qui montre que rg(L) < n.

∙ Supposons que rg(L) < n et prenons X≠0 appartenant à KerL. Alors

i j j i ∀i,j ∈ [[1;n]], (A B - B A )X = 0.

Ceci reste vrai pour i,j ∈ [[0;n - 1]]. En combinant linéairement ces égalités, on obtient

∀P,Q ∈ C [X ], (P(A)Q (B )- Q(B )P (A))X = 0. n- 1

Plus généralement,

∀P,Q ∈ C[X ], (P(A)Q (B )- Q(B )P (A))X = 0

résultat qu’on obtient en effectuant la division euclidienne de P par χA et Q par χB.

L’ensemble {P ∈ C[X],P(A)X = 0} est un idéal de C[X], dont on note μA,X l’unique générateur unitaire. Comme X est non nul, μA,X est non constant, donc admet une racine λ. Écrivons alors

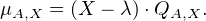
μA,X = (X - λ)⋅QA,X.

Posons Y = QA,X(A)X. Puisque QA,X est de degré strictement inférieur à celui de μA,X, on a Y ≠ 0. Par ailleurs, on a :

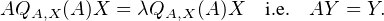
AQA,X (A )X = λQA,X (A )X i.e. AY = Y.

L’ensemble {P ∈ C[X],P(B)Y = 0} est également un idéal de C[X] dont on note μB,Y l’unique générateur unitaire. De la même manière, on note μ une racine de ce polynôme qu’on écrit alors

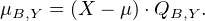
μB,Y = (X - μ)⋅QB,Y .
Posons Z = QB,Y (B)Y. On a encore Z≠0 et BZ = μZ. De plus
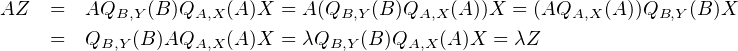
AZ=AQB,Y(B)QA,X (A )X = A(QB,Y(B )QA,X (A))X = (AQA,X (A ))QB,Y (B)X =QB,Y(B )AQA,X (A )X = λQB,Y(B )QA,X (A)X = λZ
Nous avons donc trouvé un vecteur propre commun à A et B.

b) Considérons l’application L : (A,B)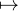↦→L(A,B), où L(A,B) est définie comme à la question a) , et l’application α : A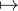↦→(A,tA). Ces deux applications sont continues, donc leur composée aussi.

Par ailleurs, considérons l’application β qui à une matrice M de taille (n(n - 1)2,n) associe le produit de tous les déterminants des matrices de taille n qu’on puisse y extraire : c’est une application continue de Mn(n-1)2,n(C) dans C, continue car polynomiale en les coefficients de M.

La composée β • L•α est continue, et, d’après la question précédente, l’ensemble des matrices A ne présentant aucun vecteur propre commun avec leur transposée est l’image réciproque de l’ouvert C* par cette application. Donc, c’est un ouvert de Mn(C).

Il nous reste à démontrer sa densité dans Mn(C). L’application φ : A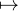↦→det(AtA -tAA) peut être considérée comme une application polynomiale à n2 indéterminées (en les coefficients de A), et à coefficients complexes. Si cette application n’est pas identiquement nulle, alors l’ensemble de ses zéros est d’intérieur vide : dans le cas contraire, on se place sur une boule ouverte non vide sur laquelle φ s’annule et on démontre, par dérivations partielles successives, que les coefficients de ce polynôme sont tous nuls. Or l’ensemble des A ayant un vecteur propre commun avec tA est inclus dans l’ensemble précédent puisque, si AX = λX et tAX = μX, (tAA - AtA)X = 0.

Il suffit pour conclure de construire, pour n ≥ 2, une matrice An telle que φ(An)≠0. Posons, pour n = 2 et n = 3,

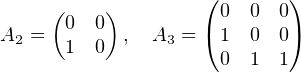
( ) (0 0) 0 0 0 A2 = 1 0 , A3 = ( 1 0 0) 0 1 1
Alors
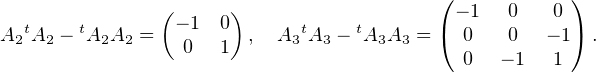
( ) ( ) tt - 1 0 t t ( - 1 0 0) A2A2- A2A2 = 0 1 , A3 A3 - A3A3 = 0 0 - 1 . 0 - 1 1
Pour n ≥ 4, il est facile de construire avec A2 et A3 une matrice diagonale par blocs An telle que φ(An )≠ 0. Ainsi φ est non nulle, ce qui montre la densité.
[Liste des corrigés]

[ < ]