 2(R) telles que detA > 1, detB > 1 et AB = BA. On
s’intéresse aux suites (vk)k
2(R) telles que detA > 1, detB > 1 et AB = BA. On
s’intéresse aux suites (vk)k N de vecteurs de R2 telles que v0≠0 et, pour tout k
N de vecteurs de R2 telles que v0≠0 et, pour tout k  N,
vk+1 = Avk ou vk+1 = Bvk. Montrer qu’il existe v0 tel que toute suite ainsi définie de
premier terme v0 soit non bornée. Le résultat subsiste-t-il si l’on omet l’hypothèse
AB = BA ?
N,
vk+1 = Avk ou vk+1 = Bvk. Montrer qu’il existe v0 tel que toute suite ainsi définie de
premier terme v0 soit non bornée. Le résultat subsiste-t-il si l’on omet l’hypothèse
AB = BA ?
Nous dirons qu’une suite (vn)n N de vecteurs de R2 est adaptée à (A,B) lorsque vn+1
N de vecteurs de R2 est adaptée à (A,B) lorsque vn+1  {Avn,Bvn}
pour tout n
{Avn,Bvn}
pour tout n  N . Nous distinguons deux cas :
N . Nous distinguons deux cas :
Cas 1 : A et B ont chacune une valeur propre double, respectivement notées λ et μ.
On a donc λ2 = detA > 1 et μ2 = detB > 1, donc |λ| > 1 et |μ| > 1. Supposons
d’abord que Ker (A - λI2) soit de dimension 1, et prenons-en un vecteur x non nul.
Comme A et B commutent, Ker(A - λI2) est stable par B, d’où Bx = μx. Posons
α := min (|λ|, |μ|) > 1. On obtient alors que toute suite v adaptée à (A,B) et telle que v0 = x a ses
termes dans V ect(x) et vérifie ∥vn∥≥ αn∥x∥ pour tout n  N. Aucune de ces suites
n’est donc bornée. Le cas où B est non-scalaire se traite de manière similaire. Si enfin A
et B sont toutes deux scalaires, il suffit évidemment de partir d’un vecteur non nul v0
arbitraire.
N. Aucune de ces suites
n’est donc bornée. Le cas où B est non-scalaire se traite de manière similaire. Si enfin A
et B sont toutes deux scalaires, il suffit évidemment de partir d’un vecteur non nul v0
arbitraire.
Cas 2 : l’une des matrices A et B a deux valeurs propres complexes distinctes. Par symétrie de la situation, on peut supposer qu’il s’agit de A. Diagonalisons A = PDP-1 où D est diagonale à valeurs diagonales distinctes. Alors B = PDʹP-1. De la commutation de A et B, on déduit facilement celle de D et Dʹ, il vient que Dʹ est diagonale en utilisant le fait que les coefficients diagonaux de D sont différents.
Les sous-espaces propres de A dans R2 sont de dimension 1, et il y en a au plus deux. On peut donc
choisir x  R 2 \ {0} qui ne soit pas vecteur propre pour A.
R 2 \ {0} qui ne soit pas vecteur propre pour A.
Considérons une suite (vn)n N adaptée à (A,B) telle que v0 = x. Notons an,bn les coefficients de
P-1 vn . Soit n
N adaptée à (A,B) telle que v0 = x. Notons an,bn les coefficients de
P-1 vn . Soit n  N. Ou bien (an+1,bn+1) = (λan,μbn), ou bien (an+1,bn+1) = (λʹan,μʹbn), où
λ, μ (respectivement, λʹ,μʹ) désigne les coefficients diagonaux de D (respectivement, de Dʹ). Ainsi
an+1 bn+1 = (detA)anbn ou an+1bn+1 = (detB)anbn. Dans tous les cas, en notant
α := min (det A, detB), on a |anbn|≥ αn|a0b0| pour tout n
N. Ou bien (an+1,bn+1) = (λan,μbn), ou bien (an+1,bn+1) = (λʹan,μʹbn), où
λ, μ (respectivement, λʹ,μʹ) désigne les coefficients diagonaux de D (respectivement, de Dʹ). Ainsi
an+1 bn+1 = (detA)anbn ou an+1bn+1 = (detB)anbn. Dans tous les cas, en notant
α := min (det A, detB), on a |anbn|≥ αn|a0b0| pour tout n  N. En outre, comme x n’est pas
vecteur propre de A, le vecteur P-1x n’est pas vecteur propre de D, si bien que a0b0≠0. Par suite
(an bn )n n’est pas bornée.
N. En outre, comme x n’est pas
vecteur propre de A, le vecteur P-1x n’est pas vecteur propre de D, si bien que a0b0≠0. Par suite
(an bn )n n’est pas bornée.
Si v était bornée la suite (P-1vn)n N serait bornée dans C2 (car y
N serait bornée dans C2 (car y  C2
C2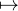 P-1y est linéaire
continue), et en prenant une borne M de cette suite au sens de la norme infinie, on aurait l’inégalité
|an bn | ≤ M2 pour tout n
P-1y est linéaire
continue), et en prenant une borne M de cette suite au sens de la norme infinie, on aurait l’inégalité
|an bn | ≤ M2 pour tout n  N. Ainsi, v n’est pas bornée.
N. Ainsi, v n’est pas bornée.
Donnons pour finir un contre-exemple dans la situation où A et B ne sont plus censées commuter.
Posons A := Diag(2-1⁄2,2), B := ρR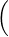
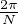
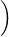 où ρ > 1 et l’entier N ≥ 3 seront ajustés
ultérieurement. On rappelle la notation R(θ) :=
où ρ > 1 et l’entier N ≥ 3 seront ajustés
ultérieurement. On rappelle la notation R(θ) := 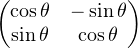 lorsque θ désigne un
réel.
lorsque θ désigne un
réel.
Clairement det A = 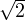 > 1 et detB = ρ2 > 1. Notons D l’ensemble des couples
(a, b)
> 1 et detB = ρ2 > 1. Notons D l’ensemble des couples
(a, b)  R 2 \ {0} tels que a + ib ait un argument dans
R 2 \ {0} tels que a + ib ait un argument dans ![[ π π]
- N, N-](/numeros/RMS130-3/RMS130-3628x.png) . Partons d’un vecteur arbitraire
v0
. Partons d’un vecteur arbitraire
v0  R 2 \ {0} et construisons (vn)n
R 2 \ {0} et construisons (vn)n N = (an,bn)n
N = (an,bn)n N par récurrence comme suit : pour tout
n
N par récurrence comme suit : pour tout
n  N , si vn
N , si vn  D on pose vn+1 := Avn, sinon on pose vn+1 := Bvn. Dans le second cas, on a
∥vn+1 ∥2 = ρ∥vn ∥2 ; dans le premier on a |bn|≤|sin(π⁄N)|∥vn∥2 et |an|≤∥vn∥2
donc
D on pose vn+1 := Avn, sinon on pose vn+1 := Bvn. Dans le second cas, on a
∥vn+1 ∥2 = ρ∥vn ∥2 ; dans le premier on a |bn|≤|sin(π⁄N)|∥vn∥2 et |an|≤∥vn∥2
donc
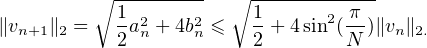
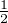 + 4sin2(
+ 4sin2(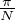 ) < 1 (ce qui est bien
sûr possible), posons δ :=
) < 1 (ce qui est bien
sûr possible), posons δ := 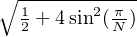 , puis choisissons ρ > 1 de telle sorte que
ρN-1 δ ≤ 1. Montrons dans ce cas que la suite v est nécessairement bornée. Notons à cet
effet
, puis choisissons ρ > 1 de telle sorte que
ρN-1 δ ≤ 1. Montrons dans ce cas que la suite v est nécessairement bornée. Notons à cet
effet
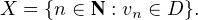
 N \ X. Notons θ l’argument de vn appartenant à
N \ X. Notons θ l’argument de vn appartenant à 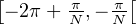 , si bien que
θ
, si bien que
θ 
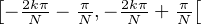 pour un k
pour un k  [ [1,N - 1]]. Il vient que n + k
[ [1,N - 1]]. Il vient que n + k  X. Par
suite, X est non majoré, deux éléments consécutifs de X sont distants d’au plus N, et
minX < N.
X. Par
suite, X est non majoré, deux éléments consécutifs de X sont distants d’au plus N, et
minX < N.
Soit n  X et m son successeur dans X. Alors vm = Bm-n-1Avn ; les calculs précédents
montrent alors que ∥vm∥2 ≤ ρm-n-1δ∥vn∥2 ≤ ρN-1δ∥vn∥2 ≤∥vn∥2 car m-n ≤ N. Ainsi, la
famille (vn )n
X et m son successeur dans X. Alors vm = Bm-n-1Avn ; les calculs précédents
montrent alors que ∥vm∥2 ≤ ρm-n-1δ∥vn∥2 ≤ ρN-1δ∥vn∥2 ≤∥vn∥2 car m-n ≤ N. Ainsi, la
famille (vn )n X est bornée pour ∥-∥2 par M := ∥vminX∥2.
X est bornée pour ∥-∥2 par M := ∥vminX∥2.
Soit enfin n  N \X. Si n < minX alors n < N donc vn = Bnv0 et ∥vn∥2 = ρn∥v0∥2 ≤ ρN-1∥v0∥2.
Sinon, on note p = max{k
N \X. Si n < minX alors n < N donc vn = Bnv0 et ∥vn∥2 = ρn∥v0∥2 ≤ ρN-1∥v0∥2.
Sinon, on note p = max{k  X : k < n}, alors n - p < N et vn = Bn-p-1Avp donc
∥vn ∥2 = ρn-p-1 δ∥vp∥2 ≤ ρN-1δM ≤ M. Ainsi, (vn)n est bornée, ce qui achève la
démonstration.
X : k < n}, alors n - p < N et vn = Bn-p-1Avp donc
∥vn ∥2 = ρn-p-1 δ∥vp∥2 ≤ ρN-1δM ≤ M. Ainsi, (vn)n est bornée, ce qui achève la
démonstration.

