 N*, A
N*, A  GLn(Z). Montrer que soit A a une valeur propre de module
strictement supérieur à 1, soit il existe k
GLn(Z). Montrer que soit A a une valeur propre de module
strictement supérieur à 1, soit il existe k  N* tel que Ak - In est nilpotente.
N* tel que Ak - In est nilpotente.
Solution de Eric Pité
Supposons que toutes les valeurs propres de 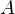 sont de module au plus
sont de module au plus 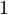 , et montrons qu’il existe
, et montrons qu’il existe
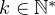 tel que
tel que  est nilpotente. Cela revient à montrer que les valeurs propres de
A sont des racines de l’unité. Il suffira alors de prendre pour k le ppcm des ordres des
racines.
est nilpotente. Cela revient à montrer que les valeurs propres de
A sont des racines de l’unité. Il suffira alors de prendre pour k le ppcm des ordres des
racines.
Les valeurs propres de A dans C comptées avec multiplicité sont λ1,…,λn, celles de Ak sont donc
λ , … , λ
, … , λ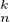 . Notons
. Notons
Pk := 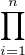 (X - λ
(X - λ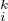 ).
).
Ainsi Pk est le polynôme caractéristique de Ak, donc Pk  Z[X]. Or les coefficients des Pk sont
uniformément bornés et dans Z donc ils prennent un nombre fini de valeurs distinctes, ainsi
l’ensemble des racines de ces polynômes est fini. Donc, pour tout i
Z[X]. Or les coefficients des Pk sont
uniformément bornés et dans Z donc ils prennent un nombre fini de valeurs distinctes, ainsi
l’ensemble des racines de ces polynômes est fini. Donc, pour tout i  [[1,n]], l’ensemble
{λ
[[1,n]], l’ensemble
{λ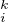 | k
| k  N * } est fini, il existe donc pi,qi
N * } est fini, il existe donc pi,qi  N* tels que pi < qi et λ
N* tels que pi < qi et λ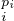 = λ
= λ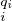 , donc les λi sont des
racines de l’unité.
, donc les λi sont des
racines de l’unité.
[Liste des corrigés]

