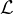47. Soient E un C-espace vectoriel de dimension finie, f (E). On dit que f est cyclique s’il existe x E tel que E = {P(f)(x);P C[X]}.

a) On suppose que f est cyclique. Montrer que tout endomorphisme induit par f est cyclique et que l’ensemble des sous-espaces de E stables par f est fini.

b) On suppose que l’ensemble des sous-espaces de E stables par f est fini. Montrer que f est cyclique.

a) Choisissons x E tel que E = {P(f)(x);P C[X]}.

∙ Soit F un sous-espace vectoriel de E stable par f et posons

Puisque f est cyclique, on a F = {P(f)(x);P I_F} et on constate que I_F est un idéal de C[X] ; il est non réduit à {0} puisqu’il contient μ_f ; soit D_F son générateur unitaire. On a donc F = {(PD_F )(f)(x);P C[X]}, soit en posant y = D_F(f).x, F = {P(f)(y);P C[X]}. Notons 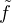l’endomorphisme de F induit par f ; on a donc F = {P( 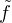)(y);P C[X]} et par conséquent 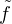est cyclique.

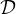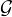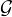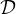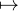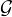∙ Notons l’ensemble (fini) des diviseurs unitaires de μ_f et l’ensemble des sous-espaces vectoriels de E stables par f. L’application D : →, FD_F est injective puisque F = {(PD_F )(f)(x);P C[X]}. Par conséquent, est également fini.

b) Redémontrons le classique

Démonstration. On suppose par l’absurde que E = G₁ ∪…∪G_s. Quitte à supposer s minimal, on peut supposer que ∀i {1,…,s}, G_i ⁄⊂⋃ _j≠iG_j.

Comme G₁ ≠ E et s ≥ 2, on dispose de a₁ G₁ \⋃ _j≠1G_j et a_s G_s \⋃ _j≠sG_j. Soit D la droite affine {(1 - t)a₁ + ta_s∣t K}. Pour i {1,…,s} soit

Comme K = T₁ ∪… ∪ T_s est infini, l’un des T_i est infini, mais alors G_i rencontre la droite D en deux points distincts (puisque a₁≠a_s) ce qui exige D ⊂ G_i. Mais alors a₁ et a_s sont tous deux dans G_i ce qui est absurde. __

Pour x E, notons F_x le plus petit sous-espace vectoriel de E stable par f et contenant x, soit F_x := {P(f)(x);P C[X]}. L’ensemble des F_x, x E, est fini et ⋃ _xEF_x = E puisque x F_x . D’après le lemme, il existe x E tel que F_x = E et f est donc cyclique.

Remarque : le résultat reste vrai sur tout corps infini.
[Liste des corrigés]