 R [X] tel que P(R+*) ⊂ R+*. Montrer qu’il existe n
R [X] tel que P(R+*) ⊂ R+*. Montrer qu’il existe n  N tel que (1 + X)nP soit
à coefficients dans R+.
N tel que (1 + X)nP soit
à coefficients dans R+.
L’exercice est difficile. Le début de la preuve est naturel et repose sur une idée classique : on étudie la factorisation en facteurs irréductibles de P dans le but de prouver le résultat pour des polynômes plus simples. Par contre, la fin de la preuve repose sur une certaine dextérité technique.
Les racines réelles d’un tel polynôme P sont négatives et son coefficient dominant est strictement positif, ainsi la factorisation de P en facteurs irréductibles ne contient que deux types de termes :
![2
X+a avec a ≥ 0 (X - b) + c avec (b,c) ∈ R× ]0,+ ∞[.](/numeros/RMS130-3/RMS130-3551x.png) |
Il suffit de prouver le résultat final lorsque P a l’une de ces deux formes réduites car la forme voulue (1 + X)n P est manifestement stable par produit. Seul le terme polynomial quadratique est délicat à gérer et l’on peut naturellement supposer que l’on a b > 0 (sinon (X - b)2 + c aurait déjà tous ses coefficients positifs). La formule du binôme de Newton permet d’arriver au calcul :
![n 2 n+2 n+1 2 2
(1+X)[(Xn - b) + c] = X + X (n - 2b)+ X(nb + nc - 2b) +(b + c)
∑k( 2 ---n!---- --------n!------- --------n!-------)
+X(b + c)k!(n - k )! - 2b(k - 1)!(n - k+ 1)! + (k- 2)!(n - k+ 2)!
k=2](/numeros/RMS130-3/RMS130-3552x.png)
 N⋆ (dépendant de b et c) tel que tous les coefficients
précédents sont positifs. Les termes extrêmes n - 2b,nb2 + nc - 2b et b2 + c ne posent aucun
problème pour n ≫ 1. Quitte à multiplier chaque coefficient par
N⋆ (dépendant de b et c) tel que tous les coefficients
précédents sont positifs. Les termes extrêmes n - 2b,nb2 + nc - 2b et b2 + c ne posent aucun
problème pour n ≫ 1. Quitte à multiplier chaque coefficient par 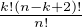 , on doit montrer pour
tout n ≫ 1 et tout k
, on doit montrer pour
tout n ≫ 1 et tout k  {2,…,n}
{2,…,n}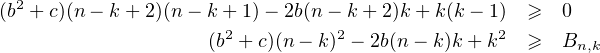
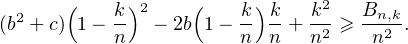 |
Posons x = 1 - 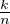
 [0,1] si bien que
[0,1] si bien que 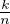 appartient également à [0,1]. Ainsi, on a Bn,k ≤
appartient également à [0,1]. Ainsi, on a Bn,k ≤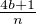 (la
partie en b2 + c n’apporte aucune contribution). Il suffit de prouver que pour tout n ≫ 1 et pour tout
x
(la
partie en b2 + c n’apporte aucune contribution). Il suffit de prouver que pour tout n ≫ 1 et pour tout
x  [0, 1] on a
[0, 1] on a
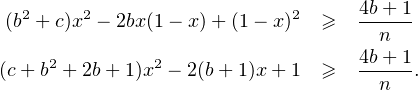
 R(c + b2 + 2b + 1)x2 - 2(b + 1)x + 1 > 0, ce qui
achève la preuve.
R(c + b2 + 2b + 1)x2 - 2(b + 1)x + 1 > 0, ce qui
achève la preuve.

