 Z[X] unitaire, irréductible dans l’anneau Z[X], ayant huit
racines de module 1 et deux racines réelles strictement positives, tel que P(0) = 1.
Z[X] unitaire, irréductible dans l’anneau Z[X], ayant huit
racines de module 1 et deux racines réelles strictement positives, tel que P(0) = 1.
L’énoncé retranscrit dans la RMS 130-2 omettait l’hypothèse voulant que P est unitaire et
demandait de trouver P irréductible dans Q[X]. Nous avons rectifié l’énoncé selon les indications
des interrogateurs de l’ENS Lyon.
Supposons temporairement l’existence d’un tel polynôme P à racines simples.
D’abord, un polynôme Q  Z[X] unitaire irréductible dans Z[X] et de degré supérieur à 2 ne peut
avoir de racine rationnelle : supposons en effet le contraire, notons r =
Z[X] unitaire irréductible dans Z[X] et de degré supérieur à 2 ne peut
avoir de racine rationnelle : supposons en effet le contraire, notons r = 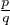 une telle racine avec
p
une telle racine avec
p  Z et q
Z et q  N * premiers entre eux, et écrivons Q = Xn +
N * premiers entre eux, et écrivons Q = Xn + 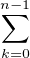 akXk où a0,…,an-1 sont entiers. Il
vient pn = -q
akXk où a0,…,an-1 sont entiers. Il
vient pn = -q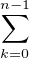 akpkqn-1-k, donc q divise pn. Comme q et p sont premiers entre
eux, il vient q∣ 1, donc q = 1. Ainsi, r est entier ; par division euclidienne on trouverait
Q = (X - r)Q1 pour un Q1
akpkqn-1-k, donc q divise pn. Comme q et p sont premiers entre
eux, il vient q∣ 1, donc q = 1. Ainsi, r est entier ; par division euclidienne on trouverait
Q = (X - r)Q1 pour un Q1  Q[X], puis par récurrence descendante on montrerait
que tous les coefficients de Q1 sont entiers. Cela contredirait l’irréductibilité de Q dans
Z[X].
Q[X], puis par récurrence descendante on montrerait
que tous les coefficients de Q1 sont entiers. Cela contredirait l’irréductibilité de Q dans
Z[X].
En particulier, ni - 1 ni 1 n’est racine de P . On note z1,…,z4,z1,…,z4 les racines de P de module
1, et x, y ses racines dans R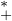 . Comme P est unitaire de degré pair et P(0) = 1, le produit des
racines de P vaut 1, donc y = x-1. On peut alors regrouper
. Comme P est unitaire de degré pair et P(0) = 1, le produit des
racines de P vaut 1, donc y = x-1. On peut alors regrouper
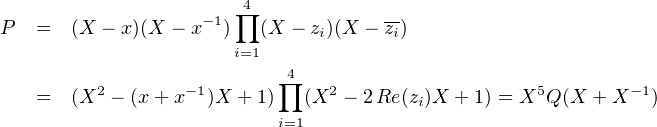
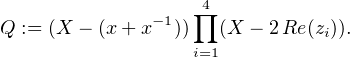
![]-1,1[](/numeros/RMS130-3/RMS130-3525x.png) . Montrons que Q doit être à coefficients dans Z, et pour cela considérons
plus généralement un polynôme P1
. Montrons que Q doit être à coefficients dans Z, et pour cela considérons
plus généralement un polynôme P1  Z[X] \{0}à racines simples sur C toutes distinctes de 1 et
- 1, et dont l’ensemble des racines est stable par inversion. En regroupant chaque racine
avec son inverse, on trouve que P1 est de degré 2n et que P1 = XnQ1(X + X-1)
pour un certain polynôme Q1
Z[X] \{0}à racines simples sur C toutes distinctes de 1 et
- 1, et dont l’ensemble des racines est stable par inversion. En regroupant chaque racine
avec son inverse, on trouve que P1 est de degré 2n et que P1 = XnQ1(X + X-1)
pour un certain polynôme Q1  C[X]. En outre, une telle écriture est unique : en effet,
étant donné Q2 tel que Q2(X + X-1) = 0, on voit par exemple que Q2 s’annule en
tout nombre complexe z (le polynôme X2 - zX + 1 ayant une racine). Remarquons
enfin que Q1 est à coefficients dans Z : en notant Q1 =
C[X]. En outre, une telle écriture est unique : en effet,
étant donné Q2 tel que Q2(X + X-1) = 0, on voit par exemple que Q2 s’annule en
tout nombre complexe z (le polynôme X2 - zX + 1 ayant une racine). Remarquons
enfin que Q1 est à coefficients dans Z : en notant Q1 = 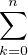 ckXk, on voit que cn est le
coefficient dominant de P1, puis une récurrence descendante montre que ck
ckXk, on voit que cn est le
coefficient dominant de P1, puis une récurrence descendante montre que ck  Z pour tout
k
Z pour tout
k  [ [ 0, n]] .
[ [ 0, n]] .
En particulier Q est à coefficients dans Z[X]. Enfin, Q doit être irréductible dans Z[X]. En effet, si
a contrario Q = CD pour des polynômes non constants C et D de Z[X], de degrés respectifs c et d,
alors P =  XcC(X + X-1)
XcC(X + X-1)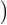
 XdD(X + X-1)
XdD(X + X-1)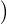 donne clairement une décomposition en produit
de deux polynômes non constants de Z[X].
donne clairement une décomposition en produit
de deux polynômes non constants de Z[X].
Ainsi, on va chercher P sous la forme X5Q(X + X-1), où Q  Z[X] vérifie les conditions
suivantes :
Z[X] vérifie les conditions
suivantes :
- Q est unitaire de degré 5 ;
- Q a quatre racines dans
![]- 2,2[](/numeros/RMS130-3/RMS130-3531x.png) et une racine dans
et une racine dans ![]2,+∞ [](/numeros/RMS130-3/RMS130-3532x.png) ;
;
- Q est irréductible dans Z[X].
Réciproquement, admettons l’existence d’un tel polynôme Q et montrons que le polynôme
P := X5 Q(X + X-1) a les propriétés requises. Évidemment P est unitaire, à coefficients entiers et
de degré 10. Ensuite, pour toute racine t de Q, les racines de X2 -tX + 1 sont racines de P : il y
en a clairement deux distinctes car t≠ ± 2 ; elles sont de module 1 et conjuguées si t 
![]- 2,2[](/numeros/RMS130-3/RMS130-3533x.png) ,
réelles strictement positives si t > 2 ; on obtient ainsi pour P huit racines distinctes de module 1 et
deux racines réelles strictement positives et distinctes de 1. Il reste à démontrer que P est
irréductible dans Z[X]. Supposons le contraire et décomposons P = AB avec A,B non
constants dans Z [X]. Comme A et B sont en particulier à coefficients réels, l’inverse de
toute racine de A de module 1 est encore racine de A (puisque c’est sa conjuguée). Par
suite, si x était racine de A mais pas x-1, alors le produit des racines de A serait x, et
donc x serait rationnel, ce qui nécessiterait que x + x-1 le soit aussi, or c’est faux car Q
n’a pas de racine rationnelle (voir la remarque initiale). Ainsi, si x est racine de A alors
x-1 l’est aussi, et de même pour B. Ainsi, chacun des polynômes A et B est scindé à
racines simples toutes différentes de ± 1, et l’ensemble de ses racines est stable par
inversion. Il vient donc A = XaC(X + X-1) et B = XbD(X + X-1) pour a :=
,
réelles strictement positives si t > 2 ; on obtient ainsi pour P huit racines distinctes de module 1 et
deux racines réelles strictement positives et distinctes de 1. Il reste à démontrer que P est
irréductible dans Z[X]. Supposons le contraire et décomposons P = AB avec A,B non
constants dans Z [X]. Comme A et B sont en particulier à coefficients réels, l’inverse de
toute racine de A de module 1 est encore racine de A (puisque c’est sa conjuguée). Par
suite, si x était racine de A mais pas x-1, alors le produit des racines de A serait x, et
donc x serait rationnel, ce qui nécessiterait que x + x-1 le soit aussi, or c’est faux car Q
n’a pas de racine rationnelle (voir la remarque initiale). Ainsi, si x est racine de A alors
x-1 l’est aussi, et de même pour B. Ainsi, chacun des polynômes A et B est scindé à
racines simples toutes différentes de ± 1, et l’ensemble de ses racines est stable par
inversion. Il vient donc A = XaC(X + X-1) et B = XbD(X + X-1) pour a := 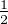 deg A,
b :=
deg A,
b := 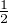 deg B, et C,D dans Z[X] de degrés respectifs a et b (donc non constants). Par suite,
(CD)(X + X-1 ) = Q(X + X-1), et il vient Q = CD par unicité de l’écriture. On
contredirait alors l’irréductibilité supposée de Q dans Z[X]. Ainsi, P est irréductible dans
Z[X].
deg B, et C,D dans Z[X] de degrés respectifs a et b (donc non constants). Par suite,
(CD)(X + X-1 ) = Q(X + X-1), et il vient Q = CD par unicité de l’écriture. On
contredirait alors l’irréductibilité supposée de Q dans Z[X]. Ainsi, P est irréductible dans
Z[X].
Il ne nous reste plus qu’à mettre en évidence un polynôme Q  Z[X] vérifiant les conditions (i) à
(iii). En s’inspirant du théorème de Rolle, on pourrait penser à introduire le polynôme dérivé de
Z[X] vérifiant les conditions (i) à
(iii). En s’inspirant du théorème de Rolle, on pourrait penser à introduire le polynôme dérivé de
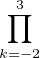 (X - k), hélas celui-ci n’est pas unitaire ! Nous utiliserons une variante de cette idée : nous
posons
(X - k), hélas celui-ci n’est pas unitaire ! Nous utiliserons une variante de cette idée : nous
posons
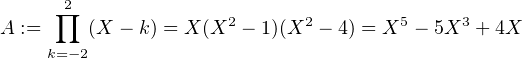
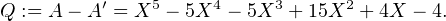
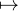 A(x)e-x, de dérivée
x
A(x)e-x, de dérivée
x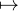 - Q(x)e-x , on voit que Q possède au moins une racine dans
- Q(x)e-x , on voit que Q possède au moins une racine dans ![]i,i+ 1[](/numeros/RMS130-3/RMS130-3541x.png) pour tout
i
pour tout
i  {-2, -1, 0, 1}. La somme des quatre racines ainsi trouvées est strictement inférieure à 3, et la
somme de toutes les racines de Q vaut 5, donc Q possède au moins une racine dans
{-2, -1, 0, 1}. La somme des quatre racines ainsi trouvées est strictement inférieure à 3, et la
somme de toutes les racines de Q vaut 5, donc Q possède au moins une racine dans ![]2,+ ∞[](/numeros/RMS130-3/RMS130-3542x.png) . La
condition (ii) est donc satisfaite.
. La
condition (ii) est donc satisfaite.
Il reste à montrer que Q est irréductible dans Z[X]. Supposons le contraire, introduisons une décomposition Q = AB, avec A et B non constants à coefficient dominant positif, et essayons de trouver une contradiction. Évidemment A et B sont unitaires (considération du coefficient dominant).
Beaucoup de coefficients de Q sont divisibles par 5, ce qui nous conduit à étudier l’irréductibilité de
Q modulo 5 : on note F5 le corps Z⁄5Z ; pour k  Z, notons k sa classe modulo 5, et pour
C =
Z, notons k sa classe modulo 5, et pour
C = 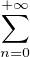 cnXn
cnXn  Z[X], notons C le polynôme
Z[X], notons C le polynôme 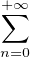 cnXn
cnXn  F5[X]. On montre facilement que
C
F5[X]. On montre facilement que
C  Z [X]
Z [X]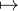 C
C  F5[X] est un morphisme d’anneaux. En particulier Q = AB, et évidemment
degA= deg A et degB = deg B puisque A et B sont unitaires. Nous avons ici Q = X5 -X + 1.
On rappelle que x5 = x pour tout x
F5[X] est un morphisme d’anneaux. En particulier Q = AB, et évidemment
degA= deg A et degB = deg B puisque A et B sont unitaires. Nous avons ici Q = X5 -X + 1.
On rappelle que x5 = x pour tout x  F5 (conséquence du théorème de Lagrange, qui indique que
x4 = 1 pour tout x dans F
F5 (conséquence du théorème de Lagrange, qui indique que
x4 = 1 pour tout x dans F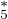 ). Ainsi Q n’a pas de racine dans F5, si bien que A et B sont précisément
les facteurs irréductibles unitaires de Q, et ils ont leur degré dans {2,3} (et ces degrés sont
distincts). Remarquons en outre que (X + 1)5 = X5 + 1 dans F5[X] grâce à la formule du binôme,
si bien que Q (X + 1) = Q(X). La transformation C
). Ainsi Q n’a pas de racine dans F5, si bien que A et B sont précisément
les facteurs irréductibles unitaires de Q, et ils ont leur degré dans {2,3} (et ces degrés sont
distincts). Remarquons en outre que (X + 1)5 = X5 + 1 dans F5[X] grâce à la formule du binôme,
si bien que Q (X + 1) = Q(X). La transformation C  F5[X]
F5[X] C(X + 1)
C(X + 1)  F5[X] est
clairement un automorphisme de l’anneau F5[X] fixant chaque polynôme constant : elle
conserve donc l’irréductibilité. Il vient Q = Q(X + 1) = A(X + 1)B(X + 1) avec
A(X + 1) et B (X + 1) irréductibles unitaires, donc A(X + 1) = A et B(X + 1) = B par
considération des degrés. C’est absurde car pour tout C
F5[X] est
clairement un automorphisme de l’anneau F5[X] fixant chaque polynôme constant : elle
conserve donc l’irréductibilité. Il vient Q = Q(X + 1) = A(X + 1)B(X + 1) avec
A(X + 1) et B (X + 1) irréductibles unitaires, donc A(X + 1) = A et B(X + 1) = B par
considération des degrés. C’est absurde car pour tout C  F5[X] unitaire de degré 2, on a
C(X + 1)≠ C(X) : en effet si a désigne le coefficient de C devant X alors celui de C(X + 1) est
a + 2.
F5[X] unitaire de degré 2, on a
C(X + 1)≠ C(X) : en effet si a désigne le coefficient de C devant X alors celui de C(X + 1) est
a + 2.
Ainsi, Q est irréductible dans Z[X], et finalement P := X5Q(X + X-1) répond à la question.
Solution d’Éric Pité
On aimerait se tourner vers les polynômes cyclotomiques, qui sont irréductibles sur Q et ont leurs
racines de module 1, malheureusement aucun n’a de racine dans R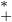 à l’exception de
X - 1.
à l’exception de
X - 1.
L’exemple qui suit est dû à Lehmer. Avec les considérations de la solution précédente, on prend Q := X5 +X4 -5X3 -5X2 +4X +3, si bien que P = X10 +X9 -X7 -X6 -X5 -X4 -X3 +X +1. Ce dernier polynôme a été trouvé par Lehmer, dans les années 1930, lors de la formulation de la conjecture portant son nom. Il est celui qui possède la plus petite mesure de Mahler (connue) strictement plus grande que 1.
La vérification des propriétés (i) et (ii) pour Q est ici effectuée par un calcul approché des zéros par
la machine (à condition d’avoir confiance en elle). Pour montrer que P est irréductible dans Z[X],
on le décompose P = AB avec A,B non constants dans Z[X]. En remarquant que P(2) = 1291 est
premier, on trouve que |A(2)| = 1 ou |B(2)| = 1. Par ailleurs on constate que |P(1)| = 1, donc
|A(1)| = |B(1)| = 1. Supposons, sans perte de généralité, que |A(1)| = |A(2)|. On remarque
par le calcul approché que la plus grande racine réelle de P est strictement inférieure à
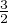 ; l’autre racine réelle est inférieure ou égale à 1 ; toute racine z de P vérifie donc
Re(z) <
; l’autre racine réelle est inférieure ou égale à 1 ; toute racine z de P vérifie donc
Re(z) < 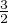 et ainsi |z - 1| < |z - 2| ; en faisant le produit de ces inégalités, on trouve
|A(1)| < |A(2)|, ce qui contredit un résultat antérieur. On conclut que P est irréductible dans Z[X].
et ainsi |z - 1| < |z - 2| ; en faisant le produit de ces inégalités, on trouve
|A(1)| < |A(2)|, ce qui contredit un résultat antérieur. On conclut que P est irréductible dans Z[X].

