24. Soient n ≥ 2 un entier, a et b deux éléments distincts de {1,…,n}, G_a,b le sous-groupe de _n engendré par la transposition τ_a,b et le cycle c := (12n). À quelle condition a-t-on G_a,b = _n  ?

Nous allons montrer que G_a,b = _n si et seulement si n et m := b - a sont premiers entre eux. Supposons, sans perte de généralité, a < b.

Montrons d’abord le caractère nécessaire de cette condition. Supposons que n et m aient un diviseur commun d > 1 (nécessairement d ≤ m < n). Pour i [ [1,d]], posons

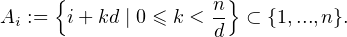
Comme d divise b - a, les entiers a et b ont même reste r modulo d, donc ils appartiennent tous deux à A_r si r≠ 0 et tous deux à A_d si r = 0. Il s’ensuit que τ_a,b(A_i) = A_i pour tout i [ [1,d]]. Par ailleurs c(A_i ) = A_i+1 pour tout i [ [1,d - 1]], et enfin c(A_d) = A₁ (le fait que d divise n implique en effet que n A_d). Les permutations τ_a,b et c appartiennent donc à l’ensemble G des permutations σ _n pour lesquelles il existe une permutation σʹ_d telle que ∀i [ [ 1, d]],σ(A_i) = A_σʹ(i). Or on vérifie facilement que G est un sous-groupe de _n  ; par ailleurs G≠_n car τ_1,2 n’est pas dans G (en effet, τ_1,2 envoie 1 dans A₂ et d + 1 dans A₁ , alors que 1 et d + 1 appartiennent tous deux à A₁). On conclut que G_a,b ≠ _n .

Dans la suite, nous supposons n ∧ m = 1 et démontrons qu’alors G_a,b = _n.

Commençons par citer un lemme technique classique dont la démonstration est élémentaire : pour tous ensembles X et Y , toute bijection σ : X → Y et tous i,j distincts dans X, l’identité σ • τ_i,j • σ^-1 = τ_σ(i),σ(j) est satisfaite.

Poursuivons par un autre résultat classique : le groupe _n est engendré par l’ensemble des transpositions de la forme τ_i,i+1 où i [ [1,n- 1]]. Soit en effet G un sous-groupe de _n contenant toutes ces transpositions. Pour tous i < j dans [ [1,n]], on voit en particulier que _n contient le cycle c_i,j := (ii + 1j - 1j) = τ_i,i+1 •• τ_j-1,j. Pour tous i,j dans [ [1,n]] tels que i < j - 1, le lemme technique rappelé plus haut assure que H contient la transposition τ_i,j = c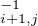 •τ_i,i+1 •c_i+1,j. Ainsi, le sous-groupe H contient toutes les transpositions de [ [1,n]], si bien que H = _n .

On notera désormais K = G_a,b. Pour simplifier la démonstration, nous allons manipuler le groupe des permutations de Z⁄nZ. On introduit la bijection canonique k {1,…,n}k Z⁄nZ, qui induit un isomorphisme de groupes Π : σ _nπ • σ • π^-1 (Z⁄nZ). Grâce à cet isomorphisme, on voit que (Z⁄nZ) est engendré par les transpositions de la forme τ_x,x+1, où x Z ⁄nZ . Pour x Z⁄nZ et k Z, on notera plus simplement x + k := x + k.

Posons c := Π(c) et τ := Π(τ_a,b), et K := Π(K). Ce dernier est donc un sous-groupe de (Z⁄nZ) contenant c et τ_a,b = τ_a,b. On observe que c : x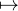x + 1, si bien que c^k : x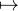x + k pour tout k Z (récurrence immédiate). Le sous-groupe K contient donc c^m • τ_a,b •c^-m = τ_a+m,b+m. En poursuivant par récurrence, on trouve que K contient τ_{a+km,a+(k+1)m} pour tout k Z .

Comme m et n sont premiers entre eux, m est inversible modulo n. Il s’ensuit que φ : x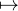a + m.x est une permutation de Z⁄nZ. L’application

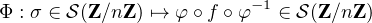
est alors un automorphisme du groupe (Z⁄nZ). On note que τ_a+mx,a+mx+m = Φ(τ_x,x+1) pour tout x Z ⁄nZ . Le sous-groupe Φ^-1(K) de (Z⁄nZ) contient donc toutes les transpositions τ_x,x+1 où x Z ⁄nZ . Il vient Φ^-1(K) = (Z⁄nZ) puis, en appliquant les isomorphismes Φ et Π^-1, on trouve successivement K = (Z⁄nZ) et K = _n, ce qui achève la démonstration.

[Liste des corrigés]