[Table des matières]
Le théorème de Lévy1
par Arnaud Basson
Lycée Lakanal, Sceaux
Résumé. Le théorème de Lévy relie la convergence en loi d’une suite de variables aléatoires à la convergence simple de leurs fonctions caractéristiques. L’objectif de l’article est de le démontrer et de mettre en perspective les outils de topologie et d’analyse fonctionnelle qui interviennent dans la preuve. On examinera ensuite quelques applications dudit théorème.
Abstract. Lévy’s continuity theorem
Lévy’s continuity theorem relates convergence in distribution of a sequence of random variables with pointwise convergence of their characteristic functions. In this paper we prove this theorem and highlight the main ideas from topology and functional analysis which underlie the proof. We also discuss some important applications of Levy’s theorem.
Mots-clés : Convergence en loi, transformation de Fourier, compacité faible, théorème central limite.
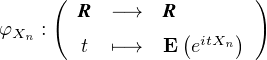
En probabilités, le théorème de Lévy11. Paul Lévy (1886-1971), mathématicien français, un des fondateurs de la théorie moderne des probabilités. Il fut professeur à l’X pendant 40 ans. (Lévy’s continuity theorem en anglais) donne une caractérisation simple et puissante de la convergence en loi des suites de variables aléatoires réelles (v.a.r.) à l’aide de leurs fonctions caractéristiques2 . Nous en donnons deux énoncés. Voici le premier, qui est assez facile à démontrer et suffira pour établir le plus célèbre corollaire du théorème de Lévy, le théorème central limite (voir § 9.2).
Théorème de Lévy (version faible).
Une suite (Xn ) de v.a.r. converge en loi vers une v.a.r. X si et seulement si la suite de leurs
fonctions caractéristiques (φXn), définies par :
La version suivante, plus puissante, est quant à elle utile dans des applications plus sophistiquées (nous en verrons quelques unes à la fin de cet article, §§ 9.3–4).
Théorème de Lévy (version forte).
Soit (Xn ) une suite de v.a.r. dont les fonctions caractéristiques φXn convergent simplement en tout
point de R vers une fonction ϕ. On suppose que ϕ est continue en 0. Alors ϕ est la fonction
caractéristique d’une v.a.r. X et la suite (Xn) converge en loi vers X.
Les principaux outils que nous introduirons pour démontrer le théorème de Lévy sont la transformation de Fourier des mesures ainsi que des propriétés de compacité faible de suites de mesures. Il ne nous semble d’ailleurs pas exagéré de dire que le théorème de Lévy est un théorème d’analyse fonctionnelle appliquée aux probabilités.
- Dans la section 2, on rappelle les définitions usuelles de la convergence en loi, illustrées d’exemples variés. La section 3 donne la définition et les propriétés fondamentales des fonctions caractéristiques de v.a.r.
- La section 4 est consacrée à la preuve de la version faible du théorème de Lévy, faisant intervenir le fameux ≪ lemme du portemanteau ≫.
- Dans la cinquième partie, on établit l’équivalence des deux définitions usuelles de la convergence en loi, puis on esquisse une première preuve de la version forte du théorème de Lévy en raisonnant avec les fonctions de répartition.
- Les parties 6 et 7 développent une autre preuve, plus longue mais à notre avis d’un intérêt plus profond, à l’aide d’arguments de topologie et d’analyse fonctionnelle qui sont en fait au cœur du théorème de Lévy. Dans la section 8 on donne quelques compléments dans cette direction en présentant très succinctement les topologies faibles dans les espaces de Banach.
- La section 9 présente quelques applications marquantes du théorème de Lévy : théorème central limite ; critère de Polya et théorème de Bochner sur les fonctions caractéristiques.
- Enfin dans la section 10, on expose d’une part quelques résultats complémentaires et on examine d’autre part la généralisation à des vecteurs aléatoires dans Rd du théorème de Lévy.
Les variables aléatoires seront définies sur un (ou si besoin plusieurs) espace(s) probabilisé(s)
(Ω, 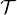 , P) ; on note E l’espérance. Sauf mention contraire (et à l’exception de P), toutes les
mesures considérées dans cet article sont des mesures boréliennes positives et finies sur
R.
, P) ; on note E l’espérance. Sauf mention contraire (et à l’exception de P), toutes les
mesures considérées dans cet article sont des mesures boréliennes positives et finies sur
R.
2.1.Les trois modes de convergence de variables aléatoires
En probabilités, l’étude asymptotique des suites de variables aléatoires fait intervenir trois principaux modes de convergence : presque sûrement, en probabilité et en loi. Nous rappelons pour mémoire les définitions des deux premiers avant de nous concentrer sur le troisième.
Définition 1.Soient Xn (n  N) et X des variables aléatoires réelles définies sur un espace
probabilisé (Ω,
N) et X des variables aléatoires réelles définies sur un espace
probabilisé (Ω, 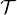 ,P).
,P).
(i) On dit que la suite (Xn) converge presque sûrement vers X si l’événement
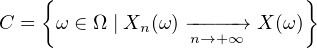
(ii) On dit que la suite (Xn) converge en probabilité vers X lorsque, quel que soit ε > 0, P
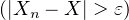
 → +∞]0.
→ +∞]0.
Il y a plusieurs façons de définir la convergence en loi. Nous donnons ici les deux plus courantes : l’une qu’on peut qualifier de définition par dualité avec des ≪ fonctions tests ≫ continues bornées, et l’autre via les fonctions de répartition. L’équivalence de ces deux définitions est non triviale et sera établie plus loin au § 5.
Définition et proposition 2. On dit qu’une suite (Xn) de v.a.r. converge en loi vers une v.a.r. X si l’une des deux propriétés équivalentes suivantes est vérifiée :
- (A)
- pour toute fonction f continue et bornée sur R, on a E
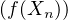
 →
+∞]E
→
+∞]E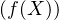 ;
;
- (B)
- la suite (Fn) des fonctions de répartition des variables Xn converge vers la fonction de répartition F de X en tout point de continuité de cette dernière.
On rappelle que la fonction de répartition d’une v.a.r. X est l’application F : R → [0,1] définie
par : F(x) = P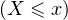 pour tout x
pour tout x  R. La propriété B ci-dessus signifie que la suite (Fn)
converge simplement vers F sur R \S, où S désigne l’ensemble des points de discontinuité de F . Il
faut noter que S est au plus dénombrable car la fonction F est croissante (c’est l’ensemble des
points où F fait un saut > 0).
R. La propriété B ci-dessus signifie que la suite (Fn)
converge simplement vers F sur R \S, où S désigne l’ensemble des points de discontinuité de F . Il
faut noter que S est au plus dénombrable car la fonction F est croissante (c’est l’ensemble des
points où F fait un saut > 0).
La convergence en loi d’une suite de variables aléatoires (parfois appelée aussi convergence en
distribution) se note généralement Xn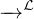 .
.
On démontre classiquement que la convergence presque sûre implique la convergence en probabilité, qui elle-même implique la convergence en loi, et que les réciproques sont fausses (voir par exemple [BL]). Le lecteur pourra expérimenter les différences entre ces trois modes de convergence en résolvant l’exercice suivant.
Exercice. Soit (Xn) une suite de v.a. de Bernoulli indépendantes. Pour tout n  N, on note
pn = P
N, on note
pn = P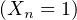 le paramètre de Xn.
le paramètre de Xn.
a. Montrer que la suite de v.a. (Xn) converge en loi si et seulement si la suite (pn) converge, et que
la limite est alors une variable de Bernoulli.
b. On suppose que (Xn) converge en probabilité. Montrer que P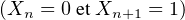 tend vers
0. En déduire que (pn) converge vers 0 ou 1. Étudier la réciproque.
tend vers
0. En déduire que (pn) converge vers 0 ou 1. Étudier la réciproque.
c. Montrer à l’aide des lemmes de Borel-Cantelli que la suite (Xn) converge presque sûrement vers
0 si et seulement si la série 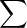 pn est convergente. En déduire une condition nécessaire et suffisante
pour que (Xn ) converge presque sûrement.
pn est convergente. En déduire une condition nécessaire et suffisante
pour que (Xn ) converge presque sûrement.
Exercice. Une suite de v.a.r. (Xn) converge en loi vers une variable constante X = a si et seulement si elle converge en probabilité vers cette constante.
2.2.Reformulation de la définition à l’aide des lois
Dans toute la suite de cet article, nous noterons μn la loi de Xn et μ la loi de X. Ce sont les mesures
de probabilité sur R définies par : pour tout borélien A ⊂ R, μn(A) = P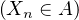 , et de même
pour μ(A). Pour mémoire, rappelons que le théorème de transfert s’énonce à l’aide de ces
mesures : étant donné une fonction borélienne f : R → R, la v.a. f(X) admet une espérance si et
seulement si f est μ-intégrable et on a alors
, et de même
pour μ(A). Pour mémoire, rappelons que le théorème de transfert s’énonce à l’aide de ces
mesures : étant donné une fonction borélienne f : R → R, la v.a. f(X) admet une espérance si et
seulement si f est μ-intégrable et on a alors
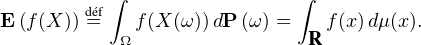
(A’) pour toute fonction f continue et bornée sur R,
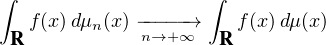
(B’) pour tout réel x tel que μ({x}) = 0, on a μn(]-∞,x])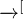 → +∞]μ(]-∞,x]).
→ +∞]μ(]-∞,x]).
Observation importante (qu’il est bon de toujours garder en tête dès qu’on parle de convergence en loi) : la convergence en loi d’une suite de variables aléatoires (Xn) ne fait intervenir que les lois de ces variables aléatoires ; c’est en fait une convergence de la suite de leurs lois, et non des variables elles-mêmes (contrairement aux deux autres modes de convergence).
Remarque. Puisque seules les lois interviennent, on peut se permettre de parler de convergence en loi pour des v.a.r. Xn et X qui ne sont pas définies sur le même espace probabilisé. D’autre part, la variable limite X n’est pas unique, seule sa loi est déterminée de manière unique. De ce fait, on emploie parfois par abus de langage des tournures abrégées du type : la suite (Xn) converge en loi vers μ (au lieu de : converge vers une variable de loi μ).
Nous admettons, pour traiter les exemples qui suivent, l’équivalence des deux définitions A et B de la convergence en loi.
- ∙
-
Cas où les variables Xn et X sont presque sûrement constantes : Xn = cn
 R pour
tout n et X = c
R pour
tout n et X = c  R.
R.
Si cn → c, alors (Xn) converge en loi vers X. En effet, en utilisant la définition A, pour toute fonction f continue et bornée sur R, on a E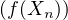 = f(cn) → f(c) = E
= f(cn) → f(c) = E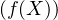 (en fait on a ici la convergence presque sûre de Xn vers X bien entendu).
(en fait on a ici la convergence presque sûre de Xn vers X bien entendu).
Réciproquement, si (Xn) converge en loi vers X, en prenant par exemple la fonction f : x
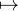 exp(-|x - c|) (fonction ayant un maximum global strict en c), on obtient
|cn - c| → 0.
exp(-|x - c|) (fonction ayant un maximum global strict en c), on obtient
|cn - c| → 0.
Cet exemple montre, au passage, la nécessité d’exclure, dans la définition B, les points de discontinuité de la fonction de répartition limite F . Si cn = 1⁄n par exemple, on voit que Fn (x) = 1x≥
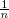 converge vers F(x) = 1x≥0 pour tout x
converge vers F(x) = 1x≥0 pour tout x  R* mais pas pour x = 0.
R* mais pas pour x = 0.
- ∙
-
Soit Un une variable de loi uniforme sur l’ensemble {0,1⁄n,2⁄n,…,1}, alors la suite suite (Un ) converge en loi vers une variable U à densité uniforme sur [0,1]. En effet, en notant δx la mesure de Dirac au point x (telle que δx({x}) = 1 et δx(R \{x}) = 0), on a ici μn =
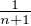 (δ0 + δ1⁄n + ... + δ1) et μ est la mesure de Lebesgue sur [0,1] ; si f est
une fonction continue, la somme de Riemann
(δ0 + δ1⁄n + ... + δ1) et μ est la mesure de Lebesgue sur [0,1] ; si f est
une fonction continue, la somme de Riemann
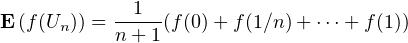
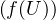 =
= 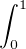 f(u)d u.
f(u)d u.
- ∙
-
Pour les variables à valeurs entières, on dispose d’un critère très simple de convergence en loi :
Lemme 1.Si les Xn et X sont à valeurs dans N, alors la suite (Xn) converge en loi vers X si et seulement si :
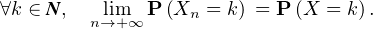
Ce lemme découle immédiatement de la définition B de la convergence en loi, en remarquant qu’une fonction de répartition de variable à valeurs dans N vérifie, pour tout x
 [k,k + 1[,
F(x) = P
[k,k + 1[,
F(x) = P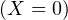 + ... + P
+ ... + P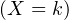 .
.
On peut en déduire de nombreux exemples de convergence en loi, par exemple le théorème de Poisson : si Xn suit une loi binomiale
 (n,pn) avec npn → λ > 0 lorsque
n → +∞, alors Xn converge en loi vers une variable de Poisson de paramètre λ. Un
autre exemple classique est fourni par les permutations aléatoires : si Xn désigne le
nombre de points fixes d’une permutation choisie aléatoirement selon la loi uniforme
dans le groupe symétrique Sn, on peut calculer la loi de Xn et vérifier que, pour
tout k
(n,pn) avec npn → λ > 0 lorsque
n → +∞, alors Xn converge en loi vers une variable de Poisson de paramètre λ. Un
autre exemple classique est fourni par les permutations aléatoires : si Xn désigne le
nombre de points fixes d’une permutation choisie aléatoirement selon la loi uniforme
dans le groupe symétrique Sn, on peut calculer la loi de Xn et vérifier que, pour
tout k  N , Pn(Xn = k) tend vers 1⁄(k!e) (on a noté Pn la probabilité uniforme sur
Sn ). Ainsi la suite (Xn) converge en loi vers une variable de Poisson de paramètre
1.
N , Pn(Xn = k) tend vers 1⁄(k!e) (on a noté Pn la probabilité uniforme sur
Sn ). Ainsi la suite (Xn) converge en loi vers une variable de Poisson de paramètre
1.
-
Exercice. Montrer que le lemme 1 s’étend au cas de variables à valeurs dans Z.
Indication pour prouver la suffisance de la condition du lemme. Étant donné ε > 0, fixer A > 0 tel que P
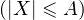 ≥ 1 - ε puis n0 tel que P
≥ 1 - ε puis n0 tel que P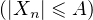 ≥ 1 - 2ε pour tout
n ≥ n0 , afin de contrôler les queues des distributions uniformément par rapport à
n.
≥ 1 - 2ε pour tout
n ≥ n0 , afin de contrôler les queues des distributions uniformément par rapport à
n.
- ∙
-
Pour des variables à densité, on dispose du résultat suivant qui fournit une condition suffisante de convergence en loi.
Théorème 1 (Scheffé). Soit (Xn) une suite de v.a.r. à densité : dμn(x) = ρn(x)d x pour tout n. Si la suite (ρn) converge presque partout vers une densité ρ, alors (Xn) converge en loi vers une variable de densité ρ.
N.B. Le fait que ρ soit d’intégrale 1 est une hypothèse indispensable de ce théorème.
Preuve succincte : l’idée consiste à remarquer que
 inf(ρn,ρ) tend vers
inf(ρn,ρ) tend vers  ρ = 1 (par
convergence dominée) ; on en déduit que
ρ = 1 (par
convergence dominée) ; on en déduit que  |ρn - ρ| tend vers 0 (grâce à l’identité
|a - b| = a + b - 2inf(a,b)) ; ceci permet de conclure aisément.
|ρn - ρ| tend vers 0 (grâce à l’identité
|a - b| = a + b - 2inf(a,b)) ; ceci permet de conclure aisément.
- ∙
-
La condition du théorème de Scheffé n’est pas nécessaire pour obtenir la convergence en loi d’une suite de variables à densité. Soit par exemple Xn la variable de densité ρn (x) = 1 + sin(2nπx) si x
 [0,1], ρn(x) = 0 sinon, alors la suite (Xn) converge en loi vers
une variable X de loi uniforme sur [0,1] (cela résulte du lemme de Riemann-Lebesgue en
appliquant la définition A).
[0,1], ρn(x) = 0 sinon, alors la suite (Xn) converge en loi vers
une variable X de loi uniforme sur [0,1] (cela résulte du lemme de Riemann-Lebesgue en
appliquant la définition A).
- ∙
-
On lance une pièce de monnaie qui tombe sur pile avec probabilité 1⁄n. Soit Xn le nombre de lancers nécessaires pour obtenir une fois pile : Xn suit la loi géométrique de paramètre 1⁄n. La fonction de répartition de la variable normalisée Y n = Xn⁄n est donnée par : FY n (x) = P
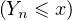 = 0 si x ≤ 0, et pour x > 0,
= 0 si x ≤ 0, et pour x > 0,
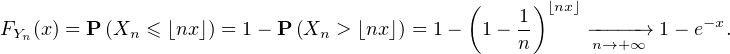
 (1).
(1).
- ∙
-
Exercice. Le problème des anniversaires.
Soit n
 N * et (Xi)i≥1 une suite de v.a. indépendantes de loi uniforme sur {1,…,n}. On pose
Tn = inf {k ≥ 1∣∃i < k, Xk = Xi} (on tire successivement des numéros au hasard dans
l’ensemble {1,…,n} jusqu’à ce qu’un même numéro apparaisse deux fois). Pour tout k
N * et (Xi)i≥1 une suite de v.a. indépendantes de loi uniforme sur {1,…,n}. On pose
Tn = inf {k ≥ 1∣∃i < k, Xk = Xi} (on tire successivement des numéros au hasard dans
l’ensemble {1,…,n} jusqu’à ce qu’un même numéro apparaisse deux fois). Pour tout k  N, on
a
N, on
a
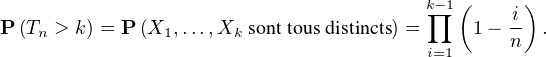
Déterminer les fonctions de répartitions de Tn puis de Tn⁄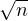 . Montrer que
. Montrer que
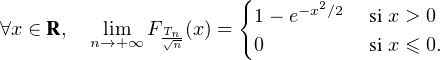
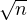 converge en loi vers une variable de densité xe-x2⁄2
sur
R
converge en loi vers une variable de densité xe-x2⁄2
sur
R (loi de Rayleigh).
(loi de Rayleigh).
3.Fonction caractéristique d’une mesure
Définition 3.La fonction caractéristique d’une mesure de probabilité μ sur R (ou plus
généralement d’une mesure finie sur R) est la fonction 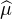 : R → R définie par
: R → R définie par
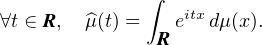
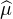 (t) = E
(t) = E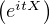 .
.
En analyse fonctionnelle, on parlerait de transformée de Fourier de la mesure finie μ (avec une
différence de signe dans l’exposant par rapport aux usages des analystes). Si μ est une
mesure à densité, alors 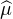 est simplement la transformée de Fourier (au sens habituel) de sa
densité.
est simplement la transformée de Fourier (au sens habituel) de sa
densité.
On trouvera en annexe de cet article une table des fonctions caractéristiques usuelles.
Propriétés évidentes : 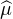 est continue sur R (par continuité sous le signe intégrale) et
bornée : |
est continue sur R (par continuité sous le signe intégrale) et
bornée : |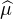 (t)| ≤
(t)| ≤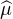 (0) = μ(R) = 1. Elle vérifie aussi
(0) = μ(R) = 1. Elle vérifie aussi 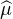 (-t) =
(-t) = 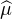 (t) pour tout réel
t.
(t) pour tout réel
t.
Exercice. Montrer que 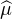 est uniformément continue sur R.
est uniformément continue sur R.
Indication : écrire |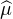 (t) -
(t) -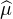 (s)|≤
(s)|≤
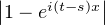 d μ(x) et utiliser le théorème de convergence
dominée.
d μ(x) et utiliser le théorème de convergence
dominée.
Exercice. a. Montrer que si μ admet un moment d’ordre n (i.e. E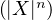 < ∞), alors
< ∞), alors 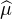 est de
classe
est de
classe  n et écrire son développement limité en 0 à l’ordre n à l’aide des moments de
μ.
n et écrire son développement limité en 0 à l’ordre n à l’aide des moments de
μ.
b. Pour n = 2, montrer réciproquement que si 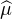 est deux fois dérivable en 0, alors μ admet une
variance finie.
est deux fois dérivable en 0, alors μ admet une
variance finie.
Indication : exprimer 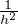 (
(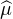 (h) - 2
(h) - 2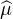 (0) +
(0) + 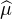 (-h)) sous forme d’une intégrale et faire tendre h vers
0.
(-h)) sous forme d’une intégrale et faire tendre h vers
0.
c. Trouver une probabilité μ n’admettant pas de moment d’ordre 1 mais telle que 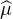 soit dérivable en
0.
soit dérivable en
0.
Indication : prendre une mesure à densité ρ(x)d x avec ρ paire et ρ(x) = C⁄(x2 ln|x|) au
voisinage de l’infini.
(De façon générale, on peut démontrer que les entiers n pour lesquels l’existence de 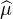 (n)(0)
entraîne la finitude de E
(n)(0)
entraîne la finitude de E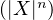 sont exactement les entiers pairs.)
sont exactement les entiers pairs.)
Comme son nom l’indique, la fonction caractéristique caractérise la loi d’une variable aléatoire.
Proposition 1.Deux v.a.r. ayant la même fonction caractéristique ont la même loi.
Autrement dit, la transformation de Fourier des mesures de probabilité sur R est injective :
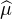 =
= 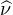
 μ = ν.
μ = ν.
Démonstration. On suppose que 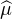 =
= 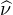 . L’idée est assez limpide : par hypothèse, l’égalité
. L’idée est assez limpide : par hypothèse, l’égalité
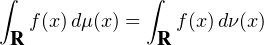
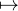 eitx ; par linéarité, c’est encore vrai pour
toute combinaison linéaire (finie) de telles exponentielles. On peut alors espérer établir cette même
égalité pour toute fonction f assez sympathique en l’exprimant comme une ≪ superposition
d’exponentielles de module 1 ≫à l’aide de sa transformée de Fourier. Il sera facile ensuite d’en
déduire l’égalité des deux mesures.
eitx ; par linéarité, c’est encore vrai pour
toute combinaison linéaire (finie) de telles exponentielles. On peut alors espérer établir cette même
égalité pour toute fonction f assez sympathique en l’exprimant comme une ≪ superposition
d’exponentielles de module 1 ≫à l’aide de sa transformée de Fourier. Il sera facile ensuite d’en
déduire l’égalité des deux mesures.
Soit f une fonction continue et intégrable sur R. Définissons sa transformée de Fourier avec la convention de signe des probabilistes :
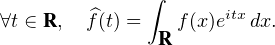
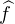 intégrable sur R elle aussi, alors d’après la formule d’inversion de Fourier, on
a
intégrable sur R elle aussi, alors d’après la formule d’inversion de Fourier, on
a
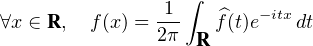
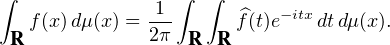
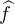
 L1(R) et μ est une mesure finie), ce qui
donne
L1(R) et μ est une mesure finie), ce qui
donne
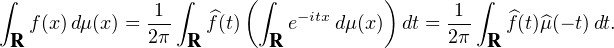
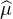 =
= 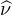 , on en déduit que
, on en déduit que
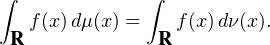
 L1(R) ∩ C0(R) telle que
L1(R) ∩ C0(R) telle que 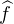
 L1(R). En particulier, c’est
valable pour toute fonction f de classe
L1(R). En particulier, c’est
valable pour toute fonction f de classe 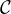 2 à support compact. En effet, pour une telle
fonction, une double intégration par parties conduit à
2 à support compact. En effet, pour une telle
fonction, une double intégration par parties conduit à 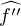 (t) = -t2
(t) = -t2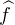 (t), or
(t), or 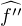 est bornée
sur R , donc
est bornée
sur R , donc 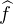 (t) = O(1⁄t2) au voisinage de ±∞. Il en résulte que
(t) = O(1⁄t2) au voisinage de ±∞. Il en résulte que 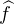 est bien intégrable
sur R .
est bien intégrable
sur R .
On en déduit ensuite que μ(]a,b[) = ν(]a,b[) pour tout intervalle ouvert borné ]a,b[, en effet on peut construire une suite (fn) de fonctions de classe C2 à support dans ]a,b[ qui converge en croissant vers la fonction indicatrice de ]a,b[, et par convergence monotone il vient
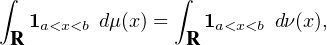
Exercice. Établir la formule d’inversion suivante pour la transformation de Fourier des mesures de probabilité : pour tous réels a et b tels que a < b,
![∫ T - ita -itb
lim1- e-----e---^μ(t)dt = 1μ ({a})+ μ(]a,b[)+ 1μ ({b}).
T→+∞2π -T it 2 2](/numeros/RMS130-3/RMS130-388x.png)
4.Le théorème de Lévy (version faible)
Si μ est une mesure finie sur R et f une fonction μ-intégrable (par exemple continue et bornée sur R), il sera commode de noter désormais ⟨f,μ⟩ l’intégrale
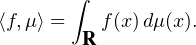
Formulée en termes de mesures, la version faible du théorème de Lévy s’énonce ainsi :
Proposition 2.Une suite (μn) de mesures de probabilité sur R converge vers une mesure
de probabilité μ au sens de la définition A’ (i.e. ⟨f,μn⟩ → ⟨f,μ⟩ pour toute fonction f
continue et bornée sur R) si et seulement si la suite des transformées de Fourier (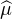 n) converge
simplement vers
n) converge
simplement vers 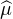 .
.
Dans cette section, nous allons démontrer cet énoncé. Ceci nous permettra déjà de mettre en évidence un certain nombre d’idées et de techniques qui sont sous-jacentes au théorème de Lévy. La preuve de la version forte, qui nécessite davantage de machinerie, sera faite plus loin.
L’implication directe étant évidente, il s’agit d’établir la réciproque. Nous supposons donc que (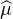 n)
converge simplement vers
n)
converge simplement vers 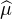 . Nous souhaitons établir la convergence, pour toute fonction f continue
et bornée sur R , ⟨f,μn⟩→⟨f,μ⟩ . Il s’agit d’un pur problème d’analyse dans lequel n’apparaît
plus aucune variable aléatoire.
. Nous souhaitons établir la convergence, pour toute fonction f continue
et bornée sur R , ⟨f,μn⟩→⟨f,μ⟩ . Il s’agit d’un pur problème d’analyse dans lequel n’apparaît
plus aucune variable aléatoire.
Nous allons prouver successivement que ⟨f,μn⟩→⟨f,μ⟩ pour f C2 à support compact, puis pour f continue à support compact et enfin pour f continue et bornée.
1ère étape : f est une fonction 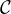 2 sur R à support compact.
2 sur R à support compact.
Par le même argument que dans la preuve de l’injectivité de la transformation de Fourier des
mesures, on établit les égalités
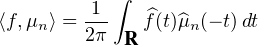
 N , et de même pour μ. La suite (
N , et de même pour μ. La suite (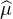 n) converge simplement vers
n) converge simplement vers 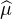 et on a la
domination
et on a la
domination 
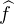 (t)
(t) n(-t)
n(-t) ≤
≤
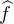 (t)
(t) , avec
, avec 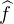
 L1(R), donc par convergence dominée il vient
⟨f, μn ⟩ → ⟨f, μ⟩.
L1(R), donc par convergence dominée il vient
⟨f, μn ⟩ → ⟨f, μ⟩.
2e étape : f est une fonction continue sur R à support compact.
On utilise un argument de densité. Soit ε > 0, il existe une fonction g 
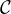 2(R) à support compact
telle que ∥f - g ∥∞≤ ε. On a alors
2(R) à support compact
telle que ∥f - g ∥∞≤ ε. On a alors  ≤ ε pour tout n, et de même avec μ (car ce
sont des mesures de masse 1). D’autre part, d’après l’étape précédente, il existe n0
≤ ε pour tout n, et de même avec μ (car ce
sont des mesures de masse 1). D’autre part, d’après l’étape précédente, il existe n0  N tel que,
pour tout n ≥ n0 , on ait
N tel que,
pour tout n ≥ n0 , on ait 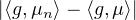 ≤ ε. Il vient alors, pour n ≥ n0,
≤ ε. Il vient alors, pour n ≥ n0, 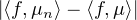 ≤ 3ε,
et on a bien établi la convergence ⟨f,μn⟩→⟨f,μ⟩.
≤ 3ε,
et on a bien établi la convergence ⟨f,μn⟩→⟨f,μ⟩.
La 3e étape est donnée par le lemme suivant.
Lemme du portemanteau. Si les μn et μ sont des mesures de probabilité sur R, il y a équivalence
entre
(i)pour toute fonction f continue et à support compact, ⟨f,μn⟩→⟨f,μ⟩ ;
(ii)pour toute fonction f continue et bornée, ⟨f,μn⟩→⟨f,μ⟩.
Démonstration du lemme. Il suffit de prouver que (i) (ii). L’idée est d’utiliser une troncature
par une fonction ψ continue à support compact et valant 1 sur un segment assez large ; le point clé
étant de trouver un segment qui convienne à la fois pour toutes les μn (au moins à partir d’un
certain rang) et μ.
(ii). L’idée est d’utiliser une troncature
par une fonction ψ continue à support compact et valant 1 sur un segment assez large ; le point clé
étant de trouver un segment qui convienne à la fois pour toutes les μn (au moins à partir d’un
certain rang) et μ.
Soit ε > 0. Il existe un segment assez grand [-A,A] tel que μ(R \ [-A,A]) ≤ ε. Soit ψ une
fonction continue, égale à 1 sur [-A,A], nulle en dehors de [-A- 1,A + 1] et telle que 0 ≤ ψ ≤ 1.
On a ⟨ψ, μ⟩ ≥ μ([-A,A]) ≥ 1 - ε. Par hypothèse, il existe un rang n0 tel que, pour tout n ≥ n0,
⟨ψ, μn ⟩ ≥ ⟨ψ, μ⟩ - ε ≥ 1 - 2ε, autrement dit
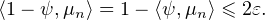
Soit maintenant f une fonction continue et bornée sur R. On écrit f = fψ + f(1 - ψ). Par hypothèse, fψ étant à support compact grâce à la troncature, on a ⟨fψ,μn⟩→⟨fψ,μ⟩. Pour n assez grand, on a donc |⟨fψ,μn⟩-⟨fψ,μ⟩|≤ ε. Pour l’autre morceau, on a
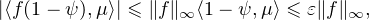
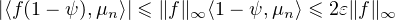
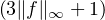 ε. Comme ε est
arbitrairement petit, ceci prouve le lemme du portemanteau. cqfd
ε. Comme ε est
arbitrairement petit, ceci prouve le lemme du portemanteau. cqfd
Commentaire. La preuve ci-dessus fonctionne car la presque totalité de la masse des mesures μn et μ est contenue dans un même compact (le support de ψ), à 2ε près : c’est le sens de l’inégalité ⟨1 - ψ, μn ⟩ ≤ 2ε, qui entraîne μn(R \ [-A- 1,A + 1]) ≤⟨1 -ψ,μn⟩≤ 2ε pour tout n ≥ n0. On dit alors que la suite de mesures (μn) est tendue. En termes intuitifs : la masse des μn au voisinage de l’infini est petite, uniformément par rapport à n. Cette propriété très importante jouera un rôle essentiel dans la suite de cet article (voir § 6).
Exercice. Montrer que si la suite (Xn) converge en loi vers X, alors la suite (φXn) converge vers φX uniformément sur tout compact.
Indication : à l’aide des mêmes idées que ci-dessus, montrer que la suite (φXn) est équicontinue.
Notations : dans toute la suite,
Cb (R ) désigne l’espace des fonctions continues et bornées sur R,
C0 (R ) désigne l’espace des fonctions continues sur R et tendant vers 0 en ±∞,
Cc (R ) désigne l’espace des fonctions continues sur R à support compact.
Ces espaces seront toujours munis de la norme uniforme ∥⋅∥∞ ; les deux premiers sont complets,
pas le troisième.
Définition 4.Soient μn et μ des mesures finies sur R (n  N). On dit que
N). On dit que
- la suite (μn ) converge étroitement vers μ si : ∀f
 Cb(R), ⟨f,μn⟩→⟨f,μ⟩ ;
Cb(R), ⟨f,μn⟩→⟨f,μ⟩ ;
- la suite (μn) converge faiblement * vers μ si : ∀f
 C0(R), ⟨f,μn⟩ → ⟨f,μ⟩
(3 ) ;
C0(R), ⟨f,μn⟩ → ⟨f,μ⟩
(3 ) ;
- la suite (μn ) converge vaguement vers μ si : ∀f
 Cc(R), ⟨f,μn⟩→⟨f,μ⟩.
Cc(R), ⟨f,μn⟩→⟨f,μ⟩.
Pour des mesures de probabilité μn et μ (ou plus généralement des mesures toutes de même masse),
ces trois convergences sont équivalentes d’après le lemme du portemanteau. Il n’en va pas de même
pour des mesures de masse quelconque, car il peut y avoir perte de masse à l’infini dans
la convergence faible * et la convergence vague. Par exemple, la suite des masses de
Dirac (δn ) converge faiblement * vers 0, mais pas étroitement. La convergence étroite
quant à elle force la conservation de la masse totale (prendre f = 1  Cb(R), il vient
μn (R ) → μ(R )).
Cb(R), il vient
μn (R ) → μ(R )).
La convergence étroite des mesures est celle qui nous intéresse car elle traduit la convergence en loi des variables aléatoires (c’est notre définition A’ du § 2). La convergence faible * est utile en analyse fonctionnelle pour ses bonnes propriétés topologiques comme on le verra par la suite. La convergence vague est rarement utilisée pour elle-même.
5.Retour aux fonctions de répartition
Avant de nous attaquer à la preuve de la version forte du théorème de Lévy, faisons un aparté pour établir l’équivalence des deux définitions A et B de la convergence en loi. On prouve en fait l’équivalence de A’ et B’ à l’aide du lemme du portemanteau. Dans tout ce qui suit, les diverses μn, et μ, sont des mesures de probabilité sur R.
Supposons la propriété B’ vérifiée : la suite des fonctions de répartition des μn converge
simplement vers celle de μ en tout point de continuité de cette dernière. Notons S l’ensemble des
points de discontinuité de la fonction de répartition de μ (c’est l’ensemble fini ou dénombrable des
atomes de μ, i.e. des réels x tels que μ({x})≠0). Pour tous a et b  R \ S tels que a < b, on
a
R \ S tels que a < b, on
a
![μn(]a,b])=μn(]- ∞, b])- μn(]- ∞, a]) → μ(]- ∞, b])- μ(]- ∞, a]) = μ(]a,b])](/numeros/RMS130-3/RMS130-3113x.png)
Passons à l’implication réciproque A’ B’. On suppose que (μn) converge étroitement vers μ, et
il s’agit d’établir la convergence ⟨f,μn⟩→⟨f,μ⟩ lorsque f est la fonction indicatrice d’une
demi-droite ]- ∞,x] avec x un réel tel que μ({x}) = 0. On va encadrer cette fonction
indicatrice par des fonctions continues en la modifiant dans un petit voisinage de x. On
a
B’. On suppose que (μn) converge étroitement vers μ, et
il s’agit d’établir la convergence ⟨f,μn⟩→⟨f,μ⟩ lorsque f est la fonction indicatrice d’une
demi-droite ]- ∞,x] avec x un réel tel que μ({x}) = 0. On va encadrer cette fonction
indicatrice par des fonctions continues en la modifiant dans un petit voisinage de x. On
a
![([ ])
1- 1-
kl→im+ ∞ μ x - k,x + k = μ({x}) = 0](/numeros/RMS130-3/RMS130-3115x.png)
![∫ ∫
0≤⟨f2,μ⟩-⟨f1,μ ⟩ = R(f2 - f1)dμ ≤ R1 [x-δ,x+δ]dμ = μ ([x- δ,x+ δ]) ≤ ε.](/numeros/RMS130-3/RMS130-3116x.png)
![⟨f1,μn⟩ ≤ ⟨1]-∞,x],μn⟩ = μn (]- ∞, x]) ≤ ⟨f2,μn ⟩,](/numeros/RMS130-3/RMS130-3117x.png)
![⟨f1,μ⟩ - ε ≤ μn(]- ∞, x]) ≤ ⟨f2,μ⟩+ ε.](/numeros/RMS130-3/RMS130-3118x.png)
 μn(]-∞,x]) - μ(]-∞,x])
μn(]-∞,x]) - μ(]-∞,x]) ≤ 3ε. Ceci prouve la
propriété B’, c’est-à-dire la convergence simple de la suite des fonctions de répartition en tout point
de continuité de la fonction de répartition de μ. cqfd
≤ 3ε. Ceci prouve la
propriété B’, c’est-à-dire la convergence simple de la suite des fonctions de répartition en tout point
de continuité de la fonction de répartition de μ. cqfd
Exercice. Montrer que si (μn) converge étroitement vers μ et que μ n’a pas d’atome (i.e. sa fonction de répartition est continue), alors la fonction de répartition de μn converge uniformément sur R vers celle de μ.
l’aide des fonctions de répartition, on peut donner une première démonstration de la version forte du théorème de Lévy. Cette preuve a l’avantage de la rapidité, mais l’inconvénient de masquer l’enracinement profond de ce théorème dans l’analyse fonctionnelle que nous mettrons en évidence plus loin. La fin de ce paragraphe est consacrée à donner les grandes lignes de cette preuve rapide. Elle repose sur le théorème suivant, qu’on peut voir comme une sorte de théorème de compacité des fonctions de répartition.
Théorème de Helly. Soit (Fn) une suite de fonctions de répartition de variables aléatoires réelles. Il existe une sous-suite (Fnk) et une fonction G : R → R continue à droite et croissante telles que (Fnk) converge simplement vers G en tout point de continuité de G.
Démonstration succincte. Les fonctions Fn sont bornées par 0 et 1. x fixé, on peut donc extraire
une sous-suite convergente de (Fn(x))n≥0. l’aide du procédé diagonal de Cantor, on peut montrer
l’existence d’une suite extraite de (Fn) qui converge en tout point x  Q (à l’aide d’une
énumération des rationnels) ; on note F : Q → R la limite simple. On pose alors, pour tout
x
Q (à l’aide d’une
énumération des rationnels) ; on note F : Q → R la limite simple. On pose alors, pour tout
x  R ,
R ,
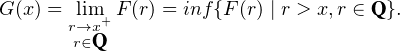
N.B. On rappelle qu’une fonction G : R → R est une fonction de répartition si et seulement si elle est croissante, continue à droite et admet pour limites 0 et 1 en -∞ et + ∞. La fonction G donnée par le théorème de Helly n’est pas nécessairement une fonction de répartition car ses limites l- et l+ en -∞ et + ∞ vérifient seulement 0 ≤ l- ≤ l+ ≤ 1. Par exemple, si Fn est la fonction indicatrice de la masse de Dirac δn au point n, alors Fn converge simplement sur R vers G = 0 qui n’est pas une fonction de répartition. On retrouve ici le phénomène de perte de masse à l’infini (la masse perdue vaut précisément 1 - (l+ - l- )).
Application à la preuve de la version forte du théorème de Lévy. On considère une suite (μn) de
probabilités sur R dont la suite des transformées de Fourier (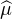 n) converge simplement vers une
fonction ϕ continue en 0. Il résulte du théorème de Helly qu’il existe une fonction G continue à
droite et croissante sur R, et une sous-suite (μnk) dont les fonctions de répartition convergent
simplement vers G en tout point de continuité de G. Pour montrer qu’il n’y a pas de perte de masse
et que G est bien la fonction de répartition d’une mesure de probabilité, on prouve que la suite de
mesures (μn ) est tendue (voir définition ). Nous ne détaillons pas cette étape ici, en effet ce point
sera établi au § 7 à l’aide d’un calcul astucieux consistant à intégrer les fonctions caractéristiques
au voisinage de 0 et utilisant la continuité de ϕ en 0. De la tension de la suite extraite
(μnk ), découle facilement l’inégalité l+ - l-≥ 1 et par suite G est bien la fonction de
répartition d’une mesure de probabilité μ ; on peut alors affirmer que (μnk) converge
étroitement vers μ (via la définition B’). Par conséquent on a
n) converge simplement vers une
fonction ϕ continue en 0. Il résulte du théorème de Helly qu’il existe une fonction G continue à
droite et croissante sur R, et une sous-suite (μnk) dont les fonctions de répartition convergent
simplement vers G en tout point de continuité de G. Pour montrer qu’il n’y a pas de perte de masse
et que G est bien la fonction de répartition d’une mesure de probabilité, on prouve que la suite de
mesures (μn ) est tendue (voir définition ). Nous ne détaillons pas cette étape ici, en effet ce point
sera établi au § 7 à l’aide d’un calcul astucieux consistant à intégrer les fonctions caractéristiques
au voisinage de 0 et utilisant la continuité de ϕ en 0. De la tension de la suite extraite
(μnk ), découle facilement l’inégalité l+ - l-≥ 1 et par suite G est bien la fonction de
répartition d’une mesure de probabilité μ ; on peut alors affirmer que (μnk) converge
étroitement vers μ (via la définition B’). Par conséquent on a 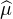 = ϕ et on est ramené à la
version faible du théorème de Lévy :
= ϕ et on est ramené à la
version faible du théorème de Lévy : 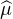 n converge simplement vers
n converge simplement vers 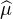 , ce qui conclut le
raisonnement.
, ce qui conclut le
raisonnement.
Réf. On trouvera les détails de cette démonstration et de la preuve du théorème de Helly dans [Bi] ou [D].
6.Compacité faible des mesures
Dans ce paragraphe et le suivant, nous donnons une preuve plus longue mais plus éclairante de la
version forte du théorème de Lévy, à l’aide d’outils d’analyse fonctionnelle. Le principe de cette
démonstration se résume ainsi : établir des propriétés de compacité faible pour la suite de lois (μn)
puis se ramener à la version faible du théorème à l’aide d’une valeur d’adhérence μ de la suite
(μn ), qui vérifiera 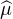 = ϕ.
= ϕ.
Nous allons d’abord établir un théorème de compacité pour la convergence faible * des mesures (dont nous verrons qu’il relève en fait de propriétés extrêmement générales des topologies faibles dans les espaces de Banach), puis un théorème de compacité pour la convergence étroite (le théorème de Prokhorov, qui est quant à lui spécifique aux mesures).
Théorème 2.Soit (μn) une suite de mesures de probabilité sur R. Il existe une suite extraite (μnk ) qui converge faiblement * vers une mesure positive μ (de masse ≤ 1).
Avantage de ce théorème : il s’applique sans aucune hypothèse restrictive (c’est presque trop beau pour être vrai !) Inconvénient : la mesure limite n’est pas nécessairement une probabilité, vu que la convergence faible * des mesures ne garantit pas la conservation de la masse totale (on a déjà vu le contre-exemple des masses de Dirac δn).
Démonstration. Le point de départ consiste à transformer les μn en des formes linéaires continues
Λn sur l’espace C0(R) en posant Λn(f) = ⟨f,μn⟩ pour toute fonction f  C0(R). On montrera
qu’il existe une sous-suite (Λnk) qui converge simplement en tout point de C0(R) vers une forme
linéaire continue Λ (c’est possible grâce à la séparabilité de l’espace C0(R)) et on conclura
grâce au théorème de représentation de Riesz qui permettra de retransformer Λ en une
mesure.
C0(R). On montrera
qu’il existe une sous-suite (Λnk) qui converge simplement en tout point de C0(R) vers une forme
linéaire continue Λ (c’est possible grâce à la séparabilité de l’espace C0(R)) et on conclura
grâce au théorème de représentation de Riesz qui permettra de retransformer Λ en une
mesure.
1ère étape. Montrons que l’espace de Banach C0(R) (muni de la norme uniforme) est séparable,
c’est-à-dire qu’il possède une partie dénombrable dense.
Le sous-espace Cc(R) est clairement dense dans C0(R), il suffit donc de trouver une famille
dénombrable de fonctions qui permet d’approcher uniformément toute fonction continue
à support compact. Soit f  Cc(R) et N
Cc(R) et N  N* un entier tel que le support de f soit
contenu dans [-N,N]. Soit ψN une fonction continue, égale à 1 sur [-N,N] et nulle en
dehors de [-N - 1,N + 1]. On sait qu’on peut approcher uniformément f sur le segment
[-N - 1, N + 1] par une suite (Pk) de polynômes de R[X]. Quitte à approcher les
coefficients de ces polynômes par des rationnels, on peut supposer que les Pk sont dans Q[X].
Alors la suite de fonctions (ψNPk)k≥0 converge uniformément vers ψNf sur R (car
ψN = 0 en dehors de [-N - 1,N + 1]). Or ψNf = f car ψN = 1 sur le support de f.
N* un entier tel que le support de f soit
contenu dans [-N,N]. Soit ψN une fonction continue, égale à 1 sur [-N,N] et nulle en
dehors de [-N - 1,N + 1]. On sait qu’on peut approcher uniformément f sur le segment
[-N - 1, N + 1] par une suite (Pk) de polynômes de R[X]. Quitte à approcher les
coefficients de ces polynômes par des rationnels, on peut supposer que les Pk sont dans Q[X].
Alors la suite de fonctions (ψNPk)k≥0 converge uniformément vers ψNf sur R (car
ψN = 0 en dehors de [-N - 1,N + 1]). Or ψNf = f car ψN = 1 sur le support de f.
Soit 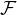 la famille dénombrable constituée des fonctions ψNP pour N
la famille dénombrable constituée des fonctions ψNP pour N  N* et P
N* et P  Q[X].
On a démontré que l’adhérence de
Q[X].
On a démontré que l’adhérence de 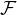 (au sens de la convergence uniforme) contient
toutes les fonctions continues à support compact, et par suite toutes les fonctions de
C0 (R ).
(au sens de la convergence uniforme) contient
toutes les fonctions continues à support compact, et par suite toutes les fonctions de
C0 (R ).
2e étape. Extraction d’une sous-suite faiblement convergente de formes linéaires.
Pour tout n  N et toute fonction f
N et toute fonction f  C0(R), on pose
C0(R), on pose
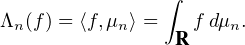
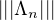 ≤ 1. Ces formes
linéaires sont en outre positives : si f ≥ 0 alors Λn(f) ≥ 0. f fixée, la suite (Λn(f)) est bornée
donc possède une sous-suite convergente. Par extraction diagonale, on peut trouver une suite extraite
(Λnk ) telle que (Λnk(f)) converge lorsque k → +∞ pour toutes les fonctions f de la
partie dénombrable dense
≤ 1. Ces formes
linéaires sont en outre positives : si f ≥ 0 alors Λn(f) ≥ 0. f fixée, la suite (Λn(f)) est bornée
donc possède une sous-suite convergente. Par extraction diagonale, on peut trouver une suite extraite
(Λnk ) telle que (Λnk(f)) converge lorsque k → +∞ pour toutes les fonctions f de la
partie dénombrable dense 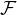 . Montrons alors que (Λnk(f)) converge pour toute fonction
f
. Montrons alors que (Λnk(f)) converge pour toute fonction
f  C0 (R ). Il faut pour cela utiliser le critère de Cauchy. Soit f
C0 (R ). Il faut pour cela utiliser le critère de Cauchy. Soit f  C0(R) et ε > 0.
Il existe g
C0(R) et ε > 0.
Il existe g 
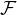 telle que ∥f - g∥∞ ≤ ε, ce qui entraîne
telle que ∥f - g∥∞ ≤ ε, ce qui entraîne  ≤ ε pour
tout n. La suite convergente (Λnk(g)) est de Cauchy, donc il existe N
≤ ε pour
tout n. La suite convergente (Λnk(g)) est de Cauchy, donc il existe N  N tel que, pour
tous j, k ≥ N,
N tel que, pour
tous j, k ≥ N, 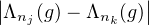 ≤ ε. On en déduit que
≤ ε. On en déduit que 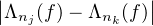 ≤ 3ε,
ainsi la suite réelle (Λnk(f)) est de Cauchy, donc converge vers une limite que nous
notons Λ(f). On voit aisément que l’application Λ ainsi définie est linéaire, positive et
continue de norme ≤ 1 (tout cela s’obtient directement par passage à la limite à partir des
Λnk ).
≤ 3ε,
ainsi la suite réelle (Λnk(f)) est de Cauchy, donc converge vers une limite que nous
notons Λ(f). On voit aisément que l’application Λ ainsi définie est linéaire, positive et
continue de norme ≤ 1 (tout cela s’obtient directement par passage à la limite à partir des
Λnk ).
3e étape. Pour conclure, on applique le théorème de représentation de Riesz, dont voici un énoncé (références : [R] ou [BP]).
Si Λ est une forme linéaire positive sur C0(R), alors il existe une (unique) mesure positive finie μ
sur R telle que, pour toute fonction f  C0(R), Λ(f) =
C0(R), Λ(f) = 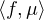 .
.
La mesure μ fournie par le théorème de Riesz vérifie bien : ∀f  C0(R),
C0(R), 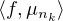 →
→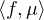 . On
peut vérifier que sa masse est inférieure ou égale à 1 en écrivant par exemple
. On
peut vérifier que sa masse est inférieure ou égale à 1 en écrivant par exemple
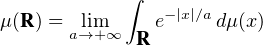
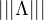 ≤ 1 :
≤ 1 :
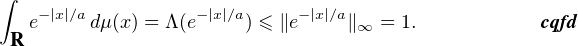 |
Nous cherchons ensuite un critère de compacité pour la convergence étroite des mesures de probabilité. La clé pour cela est la notion de tension d’une famille de mesures, que nous avons déjà rencontrée en lien avec le lemme du portemanteau.
Définition 5.Une suite (μn)n N de mesures de probabilité sur R est dite tendue si, quel
que soit ε > 0, il existe un compact K ⊂ R tel que : ∀n
N de mesures de probabilité sur R est dite tendue si, quel
que soit ε > 0, il existe un compact K ⊂ R tel que : ∀n  N, μn(R \ K) ≤ ε.
N, μn(R \ K) ≤ ε.
Tout compact de R étant contenu dans un segment, la condition de tension peut s’écrire manière équivalente :
![∀ε > 0, ∃a > 0,∀n ∈ N, μn(R \[- a,a]) ≤ ε.](/numeros/RMS130-3/RMS130-3138x.png)
Théorème de Prokhorov. De toute suite tendue (μn) de mesures de probabilité sur R, on peut extraire une sous-suite qui converge étroitement.
N.B. La limite est nécessairement une mesure de probabilité (car la convergence étroite conserve la masse).
Démonstration. Le théorème précédent fournit déjà une sous-suite (μnk) qui converge faiblement
* vers une mesure positive μ. Grâce à la propriété de tension, on va montrer que μ(R) = 1. On
pourra alors conclure à l’aide du lemme du portemanteau que (μnk) converge étroitement vers μ.
Le seul point restant à prouver est donc la conservation de la masse. On sait déjà que
μ(R ) ≤ 1. Soit ε > 0 et K un compact tel que μn(K) ≥ 1 - ε pour tout n. Soit ψ une
fonction continue à support compact telle que 0 ≤ ψ ≤ 1 sur R et ψ = 1 sur K. On a
 ≥ μnk (K) ≥ 1 - ε, d’où par convergence faible *,
≥ μnk (K) ≥ 1 - ε, d’où par convergence faible *,  ≥ 1 - ε. D’autre part
≥ 1 - ε. D’autre part
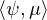 ≤ ∥ψ∥∞ μ(R) = μ(R), ainsi μ(R) ≥ 1 - ε. Ceci est valable pour tout ε > 0, d’où le
résultat. cqfd
≤ ∥ψ∥∞ μ(R) = μ(R), ainsi μ(R) ≥ 1 - ε. Ceci est valable pour tout ε > 0, d’où le
résultat. cqfd
Remarque. C’est un théorème très important, et fortement généralisable (on peut remplacer R par un espace métrique complet séparable muni de sa tribu borélienne). Il possède de nombreuses applications, notamment à la construction du mouvement brownien.
7.Fin de la preuve de la version forte du théorème de Lévy
On considère une suite (μn) de mesures de probabilité sur R, dont la suite des fonctions
caractéristiques (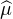 n) converge simplement sur R vers une fonction ϕ continue en 0. On veut
prouver que ϕ est la fonction caractéristique d’une mesure de probabilité μ et que (μn) converge
étroitement vers μ. Pour cela, il nous reste essentiellement à montrer que la suite (μn)
est tendue. Une fois ce point acquis, on obtiendra grâce au théorème de Prokhorov une
sous-suite (μnk ) convergeant étroitement vers une probabilité μ. On pourra alors écrire
ϕ = lim
n) converge simplement sur R vers une fonction ϕ continue en 0. On veut
prouver que ϕ est la fonction caractéristique d’une mesure de probabilité μ et que (μn) converge
étroitement vers μ. Pour cela, il nous reste essentiellement à montrer que la suite (μn)
est tendue. Une fois ce point acquis, on obtiendra grâce au théorème de Prokhorov une
sous-suite (μnk ) convergeant étroitement vers une probabilité μ. On pourra alors écrire
ϕ = lim 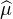 nk =
nk = 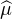 . Ainsi ϕ sera bien la fonction caractéristique d’une probabilité, et on conclura à
l’aide de la version faible du théorème de Lévy que (μn) converge étroitement vers
μ.
. Ainsi ϕ sera bien la fonction caractéristique d’une probabilité, et on conclura à
l’aide de la version faible du théorème de Lévy que (μn) converge étroitement vers
μ.
Pour obtenir la tension de la suite (μn), on utilise un calcul astucieux :
Lemme 2.Soit ν une mesure de probabilité sur R. Pour tout α > 0, on a
![1 ∫ α 1 ( [ 2 2])
--- (1- ^ν(t))dt ≥ -ν R\ ---,--
2α -α 2 α α](/numeros/RMS130-3/RMS130-3145x.png)
Démonstration. C’est calculatoire. Le théorème de Fubini nous permet d’écrire
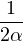 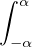 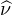 (t)d t (t)d t | = 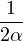 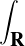 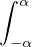 eitx d td ν(x) eitx d td ν(x) | ||
= 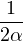 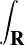 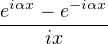 d ν(x) = d ν(x) = 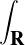 sinc(αx)d ν(x) sinc(αx)d ν(x) |
(où sinc (x) = sin x⁄x désigne la fonction sinus cardinal et sinc(0) = 1). Par suite,
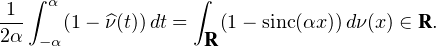
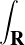  1 - sinc(αx) 1 - sinc(αx) d ν(x) d ν(x) | ≥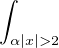  1 - sinc(αx) 1 - sinc(αx) d ν(x) d ν(x) | ||
≥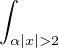  d ν(x) = d ν(x) =  ν ν![( [ 2 2])
R \ -α-,α-](/numeros/RMS130-3/RMS130-3166x.png) . . | cqfd |
Nous pouvons maintenant achever la preuve du théorème de Lévy. Observons d’emblée que la
limite simple ϕ de la suite (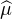 n) est une fonction borélienne bornée par 1 sur R (car les
n) est une fonction borélienne bornée par 1 sur R (car les 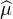 n sont
continues et
n sont
continues et 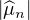 ≤ 1). On souhaite appliquer le lemme aux mesures μn. Le théorème de
convergence dominée montre que
≤ 1). On souhaite appliquer le lemme aux mesures μn. Le théorème de
convergence dominée montre que
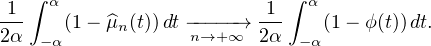
 |1 - ϕ(t)|≤ ε. Il vient alors
|1 - ϕ(t)|≤ ε. Il vient alors
![( [ 2 2])
μn R\ -α-,α- ≤ 4ε.](/numeros/RMS130-3/RMS130-3173x.png)
Remarques.
- On pourra observer que la continuité en 0 de la partie réelle de ϕ suffit à conclure,
mais c’est anecdotique. Il importe par contre de souligner que cette hypothèse de
continuité en 0 est indispensable dans le thérorème de Lévy, comme le montre le
contre-exemple suivant. Soit ρ(x)d x une mesure de probabilité à densité sur R.
Étalons-la progressivement sur R en posant, pour tout n
 N*, d μn(x) =
N*, d μn(x) = 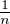 ρ(
ρ(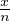 )d x,
alors les μn sont des mesures de probabilité dont les fonctions caractéristiques sont
données par
)d x,
alors les μn sont des mesures de probabilité dont les fonctions caractéristiques sont
données par 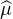 n(t) =
n(t) = 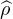 (nt). Or
(nt). Or 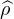 (0) = 1 et
(0) = 1 et 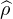 (u) → 0 quand u → ±∞, donc la
suite (
(u) → 0 quand u → ±∞, donc la
suite (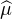 n ) converge simplement vers la fonction 1t=0, discontinue en 0. Cette dernière
n’est pas une fonction caractéristique et la suite (μn) ne converge donc pas étroitement.
Signalons néanmoins qu’elle converge faiblement * vers 0 (vérification directe aisée).
n ) converge simplement vers la fonction 1t=0, discontinue en 0. Cette dernière
n’est pas une fonction caractéristique et la suite (μn) ne converge donc pas étroitement.
Signalons néanmoins qu’elle converge faiblement * vers 0 (vérification directe aisée).
- On peut interpréter la version faible du théorème de Lévy comme une simple propriété
de continuité : la transformation de Fourier μ
 et surtout sa réciproque sont des
bijections (séquentiellement) continues entre l’ensemble des mesures de probabilité
sur R muni de la convergence étroite, et l’ensemble des fonctions caractéristiques muni
de la convergence simple (voir la prop. 2 du § 4). La version forte du théorème de Lévy
s’interprète quant à elle plutôt comme un théorème de compacité. En effet comme on
l’a vu ci-dessus, l’hypothèse de continuité de ϕ = lim
et surtout sa réciproque sont des
bijections (séquentiellement) continues entre l’ensemble des mesures de probabilité
sur R muni de la convergence étroite, et l’ensemble des fonctions caractéristiques muni
de la convergence simple (voir la prop. 2 du § 4). La version forte du théorème de Lévy
s’interprète quant à elle plutôt comme un théorème de compacité. En effet comme on
l’a vu ci-dessus, l’hypothèse de continuité de ϕ = lim n en 0 entraîne la tension de
la suite (μn ), ce qui est un critère de compacité pour la convergence étroite.
n en 0 entraîne la tension de
la suite (μn ), ce qui est un critère de compacité pour la convergence étroite.
8.Convergence et compacité faibles dans un espace de Banach
La lecture de ce paragraphe n’est pas nécessaire pour la suite de l’article ; le lecteur peut passer directement au § 9 consacré aux applications du théorème de Lévy.
Le théorème vu au § 6 est un exemple typique de théorème de compacité faible dans un espace de Banach. Un tel résultat s’inscrit dans le cadre général de l’étude des topologies faibles dans les espaces de Banach. Après avoir introduit l’espace des mesures signées, nous donnerons un bref aperçu de ce contexte général, afin de bien situer la portée des raisonnements du § 6.
Rappelons tout de suite que si E désigne un espace de Banach, son dual topologique Eʹ est l’espace
des formes linéaires continues sur E, muni de la norme subordonnée  ; c’est aussi un espace
de Banach.
; c’est aussi un espace
de Banach.
8.1.L’espace de Banach des mesures signées sur R
On peut définir des mesures signées sur R (ou sur tout ensemble muni d’une tribu  ) simplement en
remplaçant, dans la définition usuelle des mesures, la condition μ :
) simplement en
remplaçant, dans la définition usuelle des mesures, la condition μ : 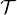 → [0,+∞] par μ :
→ [0,+∞] par μ : 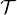 → R, et
en conservant les autres axiomes (avec convergence absolue des séries qui apparaissent dans la
propriété d’additivité dénombrable). Ces mesures signées peuvent donc prendre des valeurs
positives et négatives, mais toujours finies.
→ R, et
en conservant les autres axiomes (avec convergence absolue des séries qui apparaissent dans la
propriété d’additivité dénombrable). Ces mesures signées peuvent donc prendre des valeurs
positives et négatives, mais toujours finies.
On démontre que si μ est une mesure signée, il existe deux mesures positives finies μ+ et μ- telles que μ = μ+ - μ- ; de plus cette décomposition est unique si l’on choisit μ+ et μ- de masses minimales (ce que nous ferons systématiquement). Il existe en outre un borélien P ⊂ R (dépendant de μ) tel que, pour tout borélien A de R,

Les mesures signées sur R forment bien entendu un espace vectoriel, noté  (R). Pour toute
mesure signée μ, on pose
(R). Pour toute
mesure signée μ, on pose
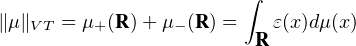
 (R), muni de cette norme
de la variation totale, est un espace de Banach.
(R), muni de cette norme
de la variation totale, est un espace de Banach.
Remarques.
- Si μ est une mesure de probabilité, on a μ+ = μ, μ- = 0 et ∥μ∥V T = μ(R) = 1.
- Si μ est une mesure signée possédant une densité ρ (par rapport à la mesure de
Lebesgue), alors μ+ et μ- ont pour densités les parties positive et négative de ρ,
définies par ρ+(x) = max(ρ(x),0) et ρ-(x) = max(-ρ(x),0). De plus, la norme de
μ vaut ∥μ∥V T =
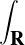
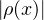 d x = ∥ρ∥L1(R).
d x = ∥ρ∥L1(R).
Le lecteur pourra maintenant revenir au théorème de Scheffé évoqué dans l’un des exemples du § 2 et constater qu’en conservant les mêmes hypothèses et la même preuve, on obtient en fait la convergence en norme de la suite des lois : ∥μn - μ ∥V T → 0. - Exercice. Vérifier que la convergence au sens de la norme ∥⋅∥V T entraîne la convergence étroite.
- Toutefois, pour des mesures ayant des atomes, la convergence en norme de la variation totale est beaucoup trop rigide : on a par exemple ∥δ1⁄n - δ0∥V T = 2 pour tout n.
Nous avons déjà vu comment associer à une mesure finie μ (éventuellement signée) une forme linéaire continue Λμ sur l’espace C0(R), en posant :
 = ∥μ∥V T. Réciproquement, si Λ est une forme linéaire continue sur
C0 (R ), alors d’après le théorème de représentation de Riesz (dans sa version pour les mesures
signées), il existe une unique mesure signée μ
= ∥μ∥V T. Réciproquement, si Λ est une forme linéaire continue sur
C0 (R ), alors d’après le théorème de représentation de Riesz (dans sa version pour les mesures
signées), il existe une unique mesure signée μ 
 (R) telle que Λ = Λμ. Il en résulte que
l’application μ
(R) telle que Λ = Λμ. Il en résulte que
l’application μ Λμ est un isomorphisme isométrique entre
Λμ est un isomorphisme isométrique entre  (R) et le dual de C0(R), au moyen
duquel on identifie ces deux espaces :
(R) et le dual de C0(R), au moyen
duquel on identifie ces deux espaces :  (R) =
(R) = 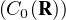 ʹ.
ʹ.
8.2.Convergence faible dans un espace de Banach et son dual
Soit E un espace de Banach et Eʹ son dual topologique (Eʹ est l’espace des formes linéaires continues sur E, muni de la norme subordonnée ; c’est aussi un espace de Banach).
Définition 6.Convergence faible dans E
Une suite (xn ) d’éléments de E converge faiblement vers x  E si :
E si :
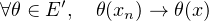
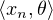 →
→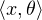 ). Notation : xn ⇀ x.
). Notation : xn ⇀ x.
Définition 7.Convergence faible * dans Eʹ(4 )
Une suite (θn ) d’éléments de Eʹ converge faiblement * vers θ  Eʹ si :
Eʹ si :
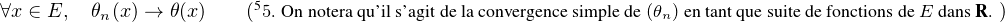
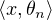 →
→ 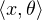 ). Notation : θn
). Notation : θn θ.
θ.
Remarque. Si E est un espace de Hilbert, il s’identifie naturellement à son dual (et le
crochet 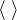 est alors le produit scalaire de E) ; les convergences faible et faible * sont alors
identiques.
est alors le produit scalaire de E) ; les convergences faible et faible * sont alors
identiques.
Quelques propriétés simples :
- Il y a unicité de la limite faible/faible * (c’est évident pour la convergence faible * dans Eʹ, un peu moins pour la convergence faible dans E : l’unicité résulte alors du théorème de Hahn-Banach).
- La convergence au sens de la norme dans E ou dans Eʹ (dite convergence forte)
implique la convergence faible (*) ; la réciproque est fausse en dimension infinie.
Voici un contre-exemple : soit H un espace de Hilbert muni d’une base hilbertienne (en )n N . Alors la suite (en) converge faiblement vers 0 dans H. En effet, pour tout
f
N . Alors la suite (en) converge faiblement vers 0 dans H. En effet, pour tout
f  H, on a ∥f∥2 =
H, on a ∥f∥2 = 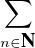
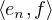 2 ; par conséquent
2 ; par conséquent 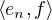 → 0. Pourtant (en) ne
converge pas fortement vers 0 puisque ∥en∥ = 1 pour tout n.
→ 0. Pourtant (en) ne
converge pas fortement vers 0 puisque ∥en∥ = 1 pour tout n.
- Une suite faiblement (*) convergente dans E ou Eʹ est bornée (au sens de la norme). C’est une application classique du théorème de Banach-Steinhaus.
Les convergences faible et faible * sont associées à des topologies dites faible et faible * sur E et Eʹ. Voir [Br] pour la définition et l’étude de ces topologies.
Cas des mesures. La ≪ convergence faible * des mesures ≫ qui a servi dans la preuve du théorème
de Lévy est en fait la convergence faible * dans l’espace dual  (R) =
(R) = 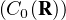 ʹ :
ʹ :
![[ ]
*
μn⇀ μ ⇐ ⇒ ∀f ∈ C0(R), ⟨f,μn⟩ → ⟨f,μ ⟩.](/numeros/RMS130-3/RMS130-3205x.png)
8.3.Quelques résultats généraux de compacité faible
Proposition 3.Soit E un espace de Banach séparable (i.e. admettant une partie dénombrable dense). Alors de toute suite bornée (θn) d’éléments de son dual Eʹ, on peut extraire une sous-suite qui converge au sens de la topologie faible *.
N.B. L’hypothèse ≪ suite bornée ≫ s’entend au sens de la norme : supn N
N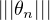 < ∞.
< ∞.
Si l’on applique cette proposition à E = C0(R), on retrouve exactement le théorème . La preuve de la proposition est d’ailleurs exactement identique à la 2e étape de celle du théorème , aussi nous ne la répéterons pas.
Pour le lecteur curieux, nous énonçons trois théorèmes qui fournissent les propriétés majeures des topologies faibles. Pour les démonstrations, voir [Br].
Théorème 3.Soit E un espace de Banach séparable. Alors la boule unité fermée de Eʹ :
BEʹ = {θ  Eʹ;
Eʹ; 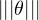 ≤ 1} est métrisable pour la topologie faible *.
≤ 1} est métrisable pour la topologie faible *.
Par contre Eʹ tout entier n’est pas métrisable pour la topologie faible * (sauf s’il est de dimension finie).
Théorème de Banach-Alaoglu. Soit E un espace de Banach, alors la boule unité fermée BEʹ de Eʹ est compacte pour la topologie faible *.
Ces deux théorèmes redémontrent en particulier la proposition donnée ci-dessus.
Enfin, pour la topologie faible sur E, on a les propriétés suivantes :
Théorème 4.Si E est un espace de Banach séparable et réflexif (E = Eʹʹ), alors sa boule unité fermée BE est compacte et métrisable pour la topologie faible.
Dans l’espace  (R), la boule unité fermée (au sens de la norme de la variation totale) est
métrisable et compacte pour la topologie faible * d’après les théorèmes ci-dessus (car
(R), la boule unité fermée (au sens de la norme de la variation totale) est
métrisable et compacte pour la topologie faible * d’après les théorèmes ci-dessus (car  (R) est le
dual de l’espace séparable C0(R)). Malheureusement le théorème 3 ne fournit pas de distance
explicite utilisable en pratique sur la boule B
(R) est le
dual de l’espace séparable C0(R)). Malheureusement le théorème 3 ne fournit pas de distance
explicite utilisable en pratique sur la boule B (R). Toutefois, si l’on se restreint au sous-ensemble
(R). Toutefois, si l’on se restreint au sous-ensemble
 de B
de B (R ) formé des mesures de probabilité, on peut construire à la main des distances
explicites qui métrisent la convergence faible * (ou la convergence étroite, ce qui revient au
même dans l’ensemble
(R ) formé des mesures de probabilité, on peut construire à la main des distances
explicites qui métrisent la convergence faible * (ou la convergence étroite, ce qui revient au
même dans l’ensemble  d’après le lemme du portemanteau), par exemple la distance de
Lévy : si μ et ν sont des mesures de probabilité de fonctions de répartition F et G, on
pose
d’après le lemme du portemanteau), par exemple la distance de
Lévy : si μ et ν sont des mesures de probabilité de fonctions de répartition F et G, on
pose
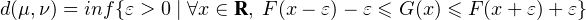
Exercice. Vérifier qu’il s’agit bien d’une distance sur l’ensemble  et que la convergence au sens
de cette distance est la convergence étroite des mesures de probabilité.
et que la convergence au sens
de cette distance est la convergence étroite des mesures de probabilité.
9.Applications du théorème de Lévy
9.1.Convergence en loi d’une somme de variables aléatoires indépendantes
Proposition 4.Soient (Xn) et (Y n) des suites de v.a.r. convergeant en loi vers des v.a.r. X et Y . Si pour chaque n les variables Xn et Y n sont indépendantes et si X est indépendante de Y , alors (Xn + Y n) converge en loi vers X + Y .
Cette propriété d’apparence très simple de la convergence en loi n’est pas du tout évidente à établir directement à partir des définitions. Par contre c’est une conséquence immédiate du théorème de Lévy (dans la version faible) : les suites de fonctions caractéristiques (φXn) et (φY n) convergent simplement vers φX et φY ; vu les hypothèses d’indépendance, la fonction caractéristique de Xn + Y n est
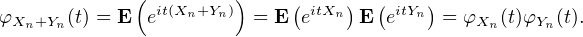
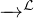 +Y .
+Y .
Remarque. En termes de mesures, on vient de démontrer que si (μn) et (νn) sont des suites de mesures de probabilité convergeant étroitement vers μ et ν, alors la suite des convolées (μn * νn) converge étroitement vers μ * ν.
Ce premier résultat, aussi simple soit-il, nous permet de mettre d’emblée le doigt sur une vaste classe d’applications du théorème de Lévy : l’étude de la convergence de sommes de variables aléatoires indépendantes. En effet, la loi (ou la fonction de répartition) d’une telle somme est souvent difficile voire impossible à calculer, tandis que sa fonction caractéristique s’obtient en faisant un simple produit, ce qui rend le théorème de Lévy extrêmement efficace dans ce cadre. La même idée est à la base de la démonstration du théorème central limite.
9.2.Le théorème central limite
Théorème central limite. Soit (Xn) une suite de v.a.r. indépendantes et identiquement distribuées,
centrées et de variance finie σ2. Alors (X1 + ... + Xn)⁄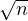 converge en loi vers une loi normale
centrée de variance σ2 :
converge en loi vers une loi normale
centrée de variance σ2 :
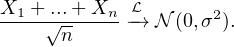
Démonstration. Elle consiste à calculer la fonction de répartition de la variable aléatoire
Zn = (X1 + ... + Xn)⁄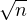 et sa limite quand n → +∞ (à l’aide d’un développement limité) afin
d’appliquer le théorème de Lévy.
et sa limite quand n → +∞ (à l’aide d’un développement limité) afin
d’appliquer le théorème de Lévy.
Notons φ la fonction caractéristique commune des Xn. Les Xn admettant un moment d’ordre 2, on peut appliquer le théorème de dérivation sous le signe intégrale à
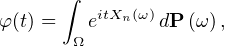
 = 0, φʹʹ(0) = -E
= 0, φʹʹ(0) = -E = -σ2. On a donc,
au voisinage de t = 0 : φ(t) = 1 - σ2t2⁄2 + o(t2).
= -σ2. On a donc,
au voisinage de t = 0 : φ(t) = 1 - σ2t2⁄2 + o(t2).
La fonction caractéristique de Zn se calcule grâce à l’hypothèse d’indépendance :
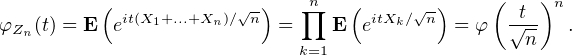
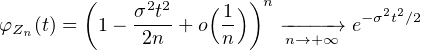
 C ; la justification de ce passage à la limite est un exercice taupinal sur
l’exponentielle complexe que nous laissons au lecteur). La limite ainsi obtenue est la fonction
caractéristique associée à la loi normale
C ; la justification de ce passage à la limite est un exercice taupinal sur
l’exponentielle complexe que nous laissons au lecteur). La limite ainsi obtenue est la fonction
caractéristique associée à la loi normale 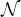 (0,σ2), d’où le résultat, en vertu de la version faible du
théorème de Lévy. cqfd
(0,σ2), d’où le résultat, en vertu de la version faible du
théorème de Lévy. cqfd
Commentaire. Le théorème central limite est bien entendu un résultat fondamental de la théorie des probabilités et des statistiques ; nous renvoyons le lecteur désireux d’en savoir plus à tout bon ouvrage traitant de ces sujets (par exemple [BL], [Bi] ou [D]).
Nous présentons maintenant quelques applications de la version forte du théorème de Lévy. Le principal intérêt de celle-ci réside dans l’étude de la classe des fonctions caractéristiques de mesures de probabilité. Le théorème de Lévy affirme essentiellement que cette classe est close par convergence simple parmi les fonctions continues en 0.
Le critère de Polya que voici fournit une condition suffisante simple d’appartenance à cette classe.
Théorème (critère de Polya). Toute fonction g : R → R continue, paire, dont la restriction à R+ est convexe et décroissante, et telle que g(0) = 1, lim+∞g = 0, est la fonction caractéristique d’une mesure de probabilité sur R.
Exemples simples connus : soit λ > 0,
- ϕ(t) = e-λ
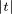 : c’est la fonction caractéristique de la loi de Cauchy de paramètre λ,
i.e. la loi à densité
: c’est la fonction caractéristique de la loi de Cauchy de paramètre λ,
i.e. la loi à densité 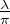 ⋅
⋅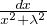 sur R.
sur R.
- ψ(t) =
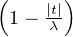 + (fonction triangle) : c’est la fonction caractéristique de la loi à
densité
+ (fonction triangle) : c’est la fonction caractéristique de la loi à
densité 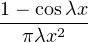 d x.
d x.
Démonstration du critère de Polya.
Montrons d’abord que le résultat est vrai si l’on suppose en plus que g est affine par morceaux et à
support compact. Une telle fonction est combinaison convexe de fonctions triangles :
g = α1 ψ1 +  + αkψk, avec ψ1,…,ψk des fonctions triangles de hauteur 1 et de largeurs
convenables et α1 ,…,αk des réels positifs de somme 1 (graphiquement : on prolonge les deux
segments extrêmes du graphe de g jusqu’à leur point d’intersection situé sur l’axe des ordonnées,
ceci donne le premier triangle α1ψ1 ; puis on retranche cette fonction à g, le reste est positif par
convexité et on réitère ce procédé pour chaque segment restant). Les ψj sont des fonctions
caractéristiques, alors g en est une aussi (cela découle du fait que l’ensemble des mesures de
probabilité est stable par combinaison convexe, et de la linéarité de la transformation de Fourier
μ
+ αkψk, avec ψ1,…,ψk des fonctions triangles de hauteur 1 et de largeurs
convenables et α1 ,…,αk des réels positifs de somme 1 (graphiquement : on prolonge les deux
segments extrêmes du graphe de g jusqu’à leur point d’intersection situé sur l’axe des ordonnées,
ceci donne le premier triangle α1ψ1 ; puis on retranche cette fonction à g, le reste est positif par
convexité et on réitère ce procédé pour chaque segment restant). Les ψj sont des fonctions
caractéristiques, alors g en est une aussi (cela découle du fait que l’ensemble des mesures de
probabilité est stable par combinaison convexe, et de la linéarité de la transformation de Fourier
μ
 ).
).
Exercice. Étant donné des v.a.r. X1,…,Xk, construire explicitement une v.a. Y telle que
φY = α1 φX1 +  + αkφXk.
+ αkφXk.
Indication : introduire une variable N indépendante des Xj et prenant les valeurs 1,…,k avec les
probabilités α1 , … ,αk.
Passons ensuite au cas général. Soit g une fonction vérifiant les hypothèses du critère de Polya. Alors on peut construire sans peine une suite (gn) de fonctions affines par morceaux à support compact, vérifiant ces mêmes hypothèses, et qui converge simplement (même uniformément) vers g sur R. D’après ce qui précède, chaque gn est la fonction caractéristique d’une v.a.r. Xn. Comme g est continue en 0, le théorème de Lévy montre que g = lim gn est une fonction caractéristique (d’une v.a. X et que Xn tend en loi vers X). □
Exemple. Soit λ > 0 et α  ]0,1[, alors h(t) = e-λ
]0,1[, alors h(t) = e-λ α
est une fonction caractéristique d’après le
critère de Polya.
α
est une fonction caractéristique d’après le
critère de Polya.
C’est vrai aussi pour α = 2 (fonction caractéristique d’une loi normale centrée).
Exercice. Montrer qu’en fait h est une fonction caractéristique pour tout α  ]0,2] en procédant
comme suit :
]0,2] en procédant
comme suit :
a. Trouver une v.a. X dont la fonction caractéristique est φX = cos. Montrer que, quel que soit
n  N , (cos )n est une fonction caractéristique.
N , (cos )n est une fonction caractéristique.
b. Soit (an ) une suite de réels positifs de somme égale à 1. Montrer que la fonction
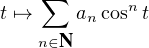
c. En déduire qu’il existe une v.a. Y dont la fonction caractéristique est donnée par l’égalité φY (t) = 1 - (1 - cost)α⁄2.
d. Trouver une suite (bn) de réels strictement positifs telle que, pour tout t  R,
R,
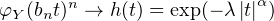
Pour α > 2, la fonction h n’est pas une fonction caractéristique (en effet elle vérifie dans ce cas
hʹʹ (0) = 0 ; s’il existait une v.a. Z telle que h = φZ, on aurait E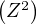 = 0 d’après un exercice du
§ 3, d’où une contradiction).
= 0 d’après un exercice du
§ 3, d’où une contradiction).
Remarque. l’aide du critère de Polya, il est facile de se convaincre qu’il existe des v.a. X et Y n’ayant pas la même loi, mais telles que φX = φY sur un intervalle [-A,A] arbitrairement large.
Le remarquable résultat suivant donne une caractérisation simple des fonctions de R dans C qui sont des fonctions caractéristiques de v.a.r. (i.e. des transformées de Fourier de mesures de probabilité sur R ).
Définition 8.Une fonction ϕ : R → C est dite définie positive si elle vérifie, pour tout N  N*,
tout N-uplet de points (t0,...,tN-1)
N*,
tout N-uplet de points (t0,...,tN-1)  RN et tout N-uplet (λ0,...,λN-1)
RN et tout N-uplet (λ0,...,λN-1)  CN de
scalaires,
CN de
scalaires,
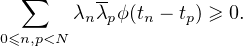 | (1) |
Théorème de Bochner. Une fonction ϕ : R → C est la fonction caractéristique d’une variable aléatoire réelle si et seulement si elle est définie positive, continue en 0 et vérifie ϕ(0) = 1.
La nécessité de ces conditions est claire : si X est une v.a.r. alors sa fonction caractéristique φX vérifie
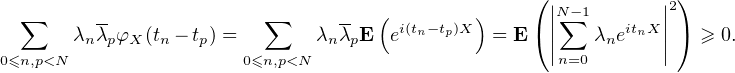
 T) et nous
assimilerons les fonctions 2π-périodiques à des fonctions définies sur T. Les coefficients de
Fourier d’une fonction f
T) et nous
assimilerons les fonctions 2π-périodiques à des fonctions définies sur T. Les coefficients de
Fourier d’une fonction f  L1(T) ou d’une mesure borélienne finie μ sur T sont définis
par
L1(T) ou d’une mesure borélienne finie μ sur T sont définis
par
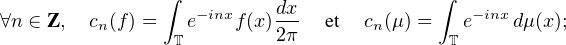
Théorème d’Herglotz. Une suite (an)n Z de nombres complexes est la suite des coefficients de
Fourier d’une mesure de probabilité μ sur T si et seulement si a0 = 1 et si la suite est définie
positive, c’est-à-dire
Z de nombres complexes est la suite des coefficients de
Fourier d’une mesure de probabilité μ sur T si et seulement si a0 = 1 et si la suite est définie
positive, c’est-à-dire
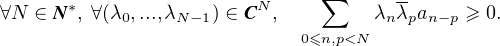
Démonstration. La nécessité de la condition se vérifie comme précédemment. Réciproquement,
soit (an )n Z une suite définie positive telle que a0 = 1. On définit, pour tous N
Z une suite définie positive telle que a0 = 1. On définit, pour tous N  N* et x
N* et x  R, en
choisissant λn = einx (0 ≤ n < N),
R, en
choisissant λn = einx (0 ≤ n < N),
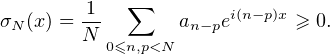
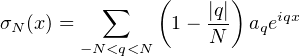
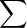 aqeiqx. On a de
plus
aqeiqx. On a de
plus
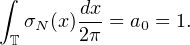
 (T) des mesures sur T), on peut extraire de la
famille (μN ) une suite (μNk)k
(T) des mesures sur T), on peut extraire de la
famille (μN ) une suite (μNk)k N qui converge faiblement * vers μ, mesure positive
sur T, c’est-à-dire : pour toute fonction f
N qui converge faiblement * vers μ, mesure positive
sur T, c’est-à-dire : pour toute fonction f  C0(T),
C0(T), 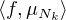 →
→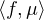 . Comme T est
compact, les convergences étroite, faible * et vague des mesures sur T sont identiques ;
en particulier on peut prendre f = 1 et constater que μ est une mesure de probabilité,
c’est-à-dire que μ(T) = limμNk(T) = 1. Prenons ensuite f : x
. Comme T est
compact, les convergences étroite, faible * et vague des mesures sur T sont identiques ;
en particulier on peut prendre f = 1 et constater que μ est une mesure de probabilité,
c’est-à-dire que μ(T) = limμNk(T) = 1. Prenons ensuite f : x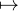 e-iqx (avec q
e-iqx (avec q  Z),
alors
Z),
alors
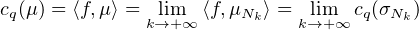
Commentaire. Voici les idées qui ont conduit à cette preuve. Si μ est une mesure de probabilité
sur T, les sommes de Fejer associées à la série de Fourier de μ, qui sont définies par
l’égalité σN,μ (x) =  (1 -|q|⁄N)cq(μ)eiqx, sont positives sur T. En effet on les
obtient en effectuant la convolution de μ avec le noyau de Fejer KN, qui est notoirement
positif :
(1 -|q|⁄N)cq(μ)eiqx, sont positives sur T. En effet on les
obtient en effectuant la convolution de μ avec le noyau de Fejer KN, qui est notoirement
positif :
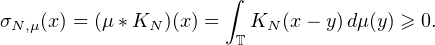
Ces observations élémentaires éclairent la démonstration effectuée ci-dessus : on ne disposait pas de la mesure μ au départ, mais on a pu définir à partir de ϕ les sommes de Fejer σN associées à la mesure cherchée, établir leur positivité grâce au caractère défini positif de ϕ et conclure à l’aide d’un argument de compacité (attendu que μ est censée être la limite des σN ).
Ces idées peuvent être transposées au cas non périodique, aussi nous suivrons la même démarche pour la preuve du théorème de Bochner, mais il y aura diverses complications techniques provenant du fait que les groupes additifs T (compact) et Z (discret) sont remplacés par R (ni compact ni discret).
Soit donc ϕ : R → C une fonction définie positive, continue en 0 et telle que ϕ(0) = 1. Il convient d’établir d’abord quelques propriétés élémentaires de ϕ.
- En prenant dans l’inégalité () de la définition, N = 2, t0 = 0, t1 = t
 R, λ0 = 1
et λ1 = 1 puis λ1 = i, on montre d’abord que ϕ(-t) = ϕ(t), puis en prenant
λ1 = -e-iarg ϕ(t), on obtient |ϕ(t)|≤ ϕ(0) = 1.
R, λ0 = 1
et λ1 = 1 puis λ1 = i, on montre d’abord que ϕ(-t) = ϕ(t), puis en prenant
λ1 = -e-iarg ϕ(t), on obtient |ϕ(t)|≤ ϕ(0) = 1.
- Maintenant, l’hypothèse () signifie que la matrice (ϕ(tn-tp))0≤n,p<N est hermitienne
positive. Prenons N = 3, (t0,t1,t2) = (0,t,s), la matrice
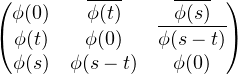
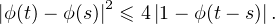
Avec l’hypothèse de continuité en 0, on en déduit que ϕ est (uniformément) continue sur R .
Maintenant nous reprenons l’idée ayant servi à prouver le théorème d’Herglotz : raisonner sur des
≪sommes de Fejer ≫. Posons, pour T > 0 et x  R,
R,
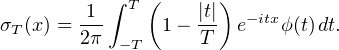
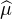 T(t) = (1 - |t|⁄T)+ϕ(t), de sorte que
T(t) = (1 - |t|⁄T)+ϕ(t), de sorte que 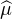 T convergera simplement vers ϕ lorsque T → +∞, et on
conclura en appliquant le théorème de Lévy (qui sert ici d’argument de compacité).
T convergera simplement vers ϕ lorsque T → +∞, et on
conclura en appliquant le théorème de Lévy (qui sert ici d’argument de compacité).
1ère étape. Commençons par la positivité de σT. Soit N  N*, posons tn = nT⁄N et λn = e-itnx
(0 ≤ n < N). L’hypothèse () s’écrit alors
N*, posons tn = nT⁄N et λn = e-itnx
(0 ≤ n < N). L’hypothèse () s’écrit alors
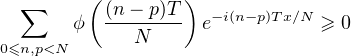
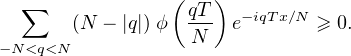
2e étape. Nous devons maintenant établir l’intégrabilité de σT. Le calcul direct de l’intégrale de σT sur R n’aboutit pas ; il faut faire une troncature. Intégrer sur un segment [-a,a] n’aboutit pas non plus, il faut être plus subtil. Considérons, pour a > 0 (grand),
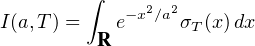
| I(a,T) | = 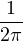  |t|≤T, x |t|≤T, x Re-x2⁄a2 Re-x2⁄a2
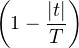 ϕ(t)e-itx d td x ϕ(t)e-itx d td x | ||
= 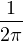 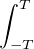 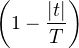 ϕ(t) ϕ(t)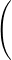 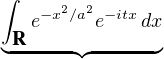 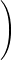 d t. d t. |
L’intégrale désignée par l’accolade est la transformée de Fourier de la gaussienne, égale à aG(at),
où G(t) = 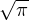 e-t2⁄4
. Lorsque a → +∞, la fonction t
e-t2⁄4
. Lorsque a → +∞, la fonction t aG(at) reste positive et d’intégrale 2π,
mais sa masse se concentre au voisinage de l’origine. On en déduit classiquement (par exemple par
changement de variable u = at et convergence dominée) que, pour toute fonction h continue et
bornée sur R ,
aG(at) reste positive et d’intégrale 2π,
mais sa masse se concentre au voisinage de l’origine. On en déduit classiquement (par exemple par
changement de variable u = at et convergence dominée) que, pour toute fonction h continue et
bornée sur R ,
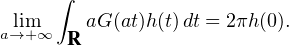
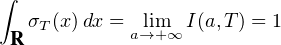
 L1(R).
L1(R).
3e étape. Nous pouvons maintenant conclure. Par définition, σT est la transformée de Fourier
inverse de h(t) = (1 -|t|⁄T)+ϕ(t) ; ces deux fonctions étant continues et intégrables sur R, le
théorème d’inversion de Fourier est applicable : la transformée de Fourier de σT est h.
En résumé, σT est positive et d’intégrale égale à 1. Elle s’identifie donc à une mesure à densité
μT , dont la fonction caractéristique est (1 -|t|⁄T)+ϕ(t). Celle-ci converge simplement
vers ϕ sur R lorsque T → +∞ et ϕ est continue en 0. Le théorème de Lévy entraîne
alors la convergence étroite de μT vers une mesure de probabilité μ vérifiant  = ϕ.
cqfd
= ϕ.
cqfd
Réf. La preuve du théorème d’Herglotz donnée ci-dessus est issue de [K], où l’on trouvera aussi une preuve du théorème de Bochner par discrétisation.
Commentaire. Comme on peut s’en douter, le théorème de Bochner n’est pas un critère pratique pour vérifier si une fonction donnée est une fonction caractéristique. Il possède néanmoins des applications importantes, notamment à l’étude des processus stochastiques stationnaires, comme le suggère l’exercice suivant.
Exercice. Soit (Xt)t R une famille de v.a.r. admettant un moment d’ordre 2. On suppose que pour
tout (t, h)
R une famille de v.a.r. admettant un moment d’ordre 2. On suppose que pour
tout (t, h)  R 2 , la fonction de covariance ϕ(h) = Cov(Xt,Xt+h) ne dépend que de h (propriété
de stationnarité). Vérifier qu’alors ϕ est définie positive.
R 2 , la fonction de covariance ϕ(h) = Cov(Xt,Xt+h) ne dépend que de h (propriété
de stationnarité). Vérifier qu’alors ϕ est définie positive.
10.1. propos de la convergence en loi
Dans l’esprit du lemme du portemanteau (voir § 4) et avec des arguments du même acabit, on démontre les caractérisations suivantes de la convergence étroite des mesures de probabilité (voir [D] pour une preuve détaillée).
Proposition 5.Soit μn et μ des mesures de probabilité sur R. Il y a équivalence entre
(i)la suite (μn) converge étroitement vers μ, i.e. ∀f  Cb(R), ⟨f,μn⟩→⟨f,μ⟩ ;
Cb(R), ⟨f,μn⟩→⟨f,μ⟩ ;
(ii)pour tout fermé F de R, limsupμn(F) ≤ μ(F) ;
(iii)pour tout ouvert O de R, liminf μn(O) ≥ μ(O) ;
(iv)pour tout borélien A ⊂ R tel que μ(∂A) = 0, limμn(A) = μ(A) ;
(v)pour toute fonction f : R → R borélienne et bornée dont l’ensemble Df des points
de discontinuité vérifie μ(Df) = 0, on a ⟨f,μn⟩→⟨f,μ⟩.
N.B. Cette proposition peut se formuler aussi avec des variables aléatoires Xn et X. Par exemple (i)
⇔ (iv) devient : (Xn) converge en loi vers X si et seulement si pour tout borélien A tel que
P = 0, on a limP
= 0, on a limP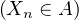 = P
= P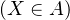 .
.
Un exposé sur la convergence en loi ne saurait être complet sans évoquer le remarquable théorème de Skorokhod.
Théorème de Skorokhod. Soit (Xn) une suite de v.a.r. qui converge en loi vers une v.a.r. X. Il
existe un espace probabilisé (Ωʹ, ʹ,Pʹ) et des v.a.r. Y n, Y définies sur cet espace telles que : pour
tout n
ʹ,Pʹ) et des v.a.r. Y n, Y définies sur cet espace telles que : pour
tout n  N , Y n a même loi que Xn, Y a même loi que X, et la suite (Y n) converge presque
sûrement vers Y .
N , Y n a même loi que Xn, Y a même loi que X, et la suite (Y n) converge presque
sûrement vers Y .
Voici les grandes lignes de la preuve de ce théorème. Elle repose sur le lemme suivant, intéressant en lui-même.
Lemme 3.Soit F : R → [0,1] la fonction de répartition d’une v.a.r. X. On pose, pour tout
u  ]0, 1[, G(u) = inf{t
]0, 1[, G(u) = inf{t  R∣F(t) ≥ u}. Soit U une v.a. de loi uniforme sur ]0,1[. Alors la
v.a. G(U) a même loi que X.
R∣F(t) ≥ u}. Soit U une v.a. de loi uniforme sur ]0,1[. Alors la
v.a. G(U) a même loi que X.
Dans le cas où F est une bijection continue et croissante de R sur ]0,1[, la fonction G est sa bijection
réciproque F-1 et le lemme est évident : pour tout x  R, P
R, P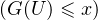 = P
= P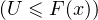 = F(x),
donc G(U) a la même fonction de répartition que X. Dans le cas où F n’est pas bijective, la
définition de G permet de montrer qu’on a encore
= F(x),
donc G(U) a la même fonction de répartition que X. Dans le cas où F n’est pas bijective, la
définition de G permet de montrer qu’on a encore
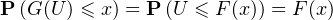
Remarque. Ce raisonnement montre un résultat un peu plus fort : toute fonction F , de R vers [0,1] croissante, continue à droite et tendant vers 0 et 1 en -∞ et + ∞ est la fonction de répartition d’une v.a.r. (à savoir de G(U)).
Pour démontrer le théorème de Skorokhod, on définit Gn, G comme dans le lemme à partir des
fonctions de répartition Fn et F des Xn et X, et on pose Y n = Gn(U), Y = G(U) (où la variable
aléatoire U suit la loi uniforme sur ]0,1[, définie sur un espace probabilisé Ωʹ quelconque). Alors
Y n et Y ont les mêmes lois que Xn et X ; on montre par ailleurs que la suite de fonctions
(Gn ) converge simplement vers G en tout point de continuité de G. Ces derniers forment
un ensemble C de complémentaire au plus dénombrable (car G est croissante), donc
Pʹ(U  C) = 1 et par suite Gn(U) → G(U) Pʹ-presque sûrement. Voir [Bi] pour les détails de la
preuve.
C) = 1 et par suite Gn(U) → G(U) Pʹ-presque sûrement. Voir [Bi] pour les détails de la
preuve.
Exercice. l’aide du théorème de Skorokhod, démontrer la proposition .
On étudie dans ce paragraphe la situation où les v.a.r. Xn sont remplacées par des vecteurs
aléatoires à valeurs dans Rd, Xn = (Xn,1,…,Xn,d) : (Ω, ,P) → Rd (ce qui revient à remplacer
les μn par des mesures de probabilité sur Rd).
,P) → Rd (ce qui revient à remplacer
les μn par des mesures de probabilité sur Rd).
La définition A (ou A’) de la convergence en loi s’étend immédiatement à une suite (Xn) de
vecteurs aléatoires dans Rd : cette suite converge vers un vecteur aléatoire X si pour toute fonction
f continue et bornée sur Rd, E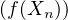 → E
→ E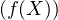 . La définition de la fonction caractéristique
s’étend aussi au cas d’un vecteur aléatoire X = (X1,…,Xd) :
. La définition de la fonction caractéristique
s’étend aussi au cas d’un vecteur aléatoire X = (X1,…,Xd) :
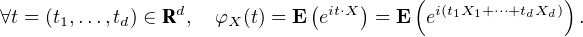
En ce qui concerne l’approche par les fonctions de répartition, elle peut aussi se généraliser à Rd, mais c’est globalement moins agréable qu’en dimension 1. La fonction de répartition FX d’un vecteur aléatoire X dans Rd est définie par
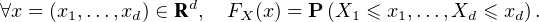
Enfin le théorème de Skorokhod reste valable lui aussi pour des suites de vecteurs aléatoires. Toutefois la démonstration que nous avons indiquée plus haut ne fonctionne plus ; la preuve en dimension d > 1, par une toute autre approche, est nettement plus compliquée (voir [Bi2]).
Annexe. Fonctions caractéristiques des lois de probabilité usuelles
Lois discrètes | p
 ]0,1[, q = 1 - p ]0,1[, q = 1 - p | ||
Bernoulli  (p) (p) | q + peit | géométrique  (p) (p) | 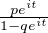 |
binomiale  (n,p) (n,p) | (q + peit)n | Poisson  (λ) (λ) | exp λ(eit - 1) λ(eit - 1) |
Remarque. Pour les variables discrètes X dont la fonction génératrice GX(s) = E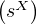 est une
série entière de rayon de convergence > 1 (c’est le cas des lois usuelles ci-dessus), la fonction
caractéristique s’obtient simplement par la relation φX(t) = GX(eit).
est une
série entière de rayon de convergence > 1 (c’est le cas des lois usuelles ci-dessus), la fonction
caractéristique s’obtient simplement par la relation φX(t) = GX(eit).
| Lois continues | densité ρ(x) | fonction caractéristique φX(t) |
normale  (m,σ2) (m,σ2) | 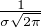 e-(x-m)2⁄2σ2 e-(x-m)2⁄2σ2
| eimte-σ2t2⁄2 |
exponentielle 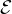 (λ) (λ) | λe-λx1x>0 | 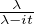 (λ > 0) (λ > 0) |
Cauchy 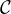 (α) (α) | 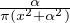 | e-α|t| (α > 0) |
uniforme 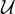 ([-a,a]) ([-a,a]) | 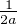 1[-a,a] 1[-a,a] | sinc(at) (a > 0) |
| triangulaire | 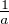  1 - 1 -  + + | sinc2 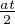  = 2 = 2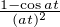 |
Bibliographie
- [Bi]
-
P. Billingsley, Probability and Measure, 3e éd. Wiley, 1995.
- [Bi2]
-
P. Billingsley, Convergence of Probability Measures, 2e éd. Wiley, 1999.
- [BL]
-
Ph. Barbe, M. Ledoux, Probabilité, 2e éd. EDP Sciences, 2007.
- [BP]
-
M. Briane, G. Pagès, Théorie de l’intégration, 4e éd. Vuibert, 2006.
- [Br]
-
H. Brézis, Analyse fonctionnelle : théorie et applications. Dunod, 1999.
- [D]
-
R. Durrett, Probability : Theory and Examples, 4e éd. Cambridge University Press, 2010.
- [K]
-
Y. Katznelson, An Introduction to Harmonic Analysis, 3e éd. Cambridge University Press, 2004.
- [R]
-
W. Rudin, Real and Complex Analysis, 3e éd. McGraw-Hill, 1987.
[Table des matières]

