18. Soit (G, .) un groupe. Si f est une fonction de G dans R, on dit que f est un quasi-morphisme s’il existe C > 0 tel que ∀(x,y) ∈ G2,|f(xy) - f(x) - f(y)|≤ C et que f est un quasi-caractère si ∀(n,x) ∈ Z × G,f(xn) = nf(x). Montrer que, pour tout quasi-morphisme M de G dans R, il existe un unique quasi-morphisme qui est aussi un quasi-caractère Q de G dans R tel que M - Q soit bornée.

Solution de Ivan Gozard

∙ Unicité
Soit Q un quasi-caractère tel que M - Q soit bornée, autrement dit tel qu’il existe K 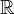∈ R+ qui vérifie : ∀g ∈ G, |M(g) - Q(g)|≤ K. Alors :

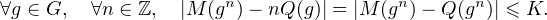
∀g∈G, ∀n ∈ Z, |M (gn) - nQ(g)| = |M (gn)- Q (gn)| ≤ K.
Soit g ∈ G. Alors
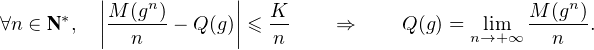
| n | n ∀n∈N*, ||M-(g-)- Q (g)||≤ K- ⇒ Q (g) = lim M-(g-). | n | n n→+∞ n

D’où l’unicité.

∙ Existence
Par une récurrence immédiate, on voit que :

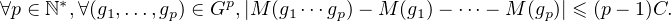
* p ∀p∈N,∀(g1,...,gp) ∈ G ,|M (g1⋅⋅⋅gp)- M (g1)- ⋅⋅⋅- M (gp)| ≤ (p - 1)C.

- Par conséquent, pour tout g ∈ G, pour tout (m,n) ∈ (N*)2, on a :

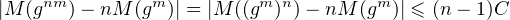
|M(gnm) - nM (gm )| = |M ((gm)n)- nM (gm)| ≤ (n - 1)C
et
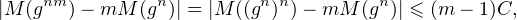
|M(gnm)- mM (gn)| = |M ((gn )n)- mM (gn)| ≤ (m - 1)C,
donc
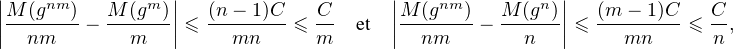
||M(gnm)M(gm )|| (n- 1)C C ||M (gnm ) M (gn)|| (m - 1)C C ||nm-m---|| ≤--mn----≤ m- et ||-nm--- - --n---|| ≤---mn--- ≤ n-,
donc
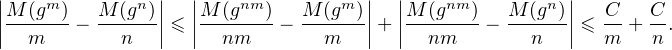
||M(gm)M(gn)|| ||M (gnm) M (gm)|| ||M (gnm) M (gn)|| C C ||m--n--|| ≤ ||-nm--- - --m---||+ ||--nm--- - --n--|| ≤ m-+ n-.
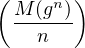Il en découle immédiatement que la suite (M (gn)) ---n--n∈N* est de Cauchy. Elle est donc convergente ; on note Q(g) sa limite.

- Pour tout g ∈ G, pour tout n ∈ N*,

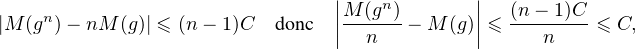
| | |M(gn)-nM (g)| ≤ (n- 1)C donc ||M-(gn)-- M (g)||≤ (n---1)C-≤ C, | n | n
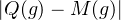d’où, en passant à la limite, |Q (g)- M (g)|≤ C.

- Notons e le neutre de G. Pour tout g ∈ G, pour tout n ∈ N*,

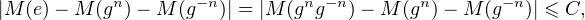
n -n n - n n - n |M(e)-M (g )- M (g )| = |M (g g )- M (g ) - M (g )| ≤ C,
donc
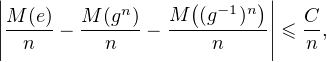
| | ||M (e) M (gn) M ((g- 1)n)|| C ||--n--- ---n-- - ----n----|| ≤ n,
d’où, en passant à la limite, Q(g-1) = -Q(g).

- Soit (g, h) ∈ G2 .

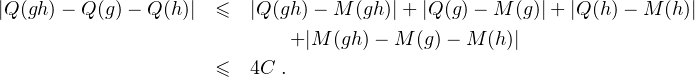
|Q(gh)-Q(g)- Q (h)| ≤ |Q (gh)- M (gh)|+ |Q(g)- M (g)|+|Q (h) - M (h)| +|M (gh )- M (g) - M (h)| ≤ 4C .

Ceci vaut pour tout (g,h) ∈ G2. Donc Q est un quasi-morphisme.

- Soit g ∈ G.

Pour tout n ∈ N* ,M(en) = M(e) donc

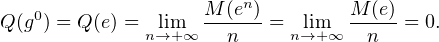
n Q (g0) = Q(e) = lim M-(e-)-= lim M-(e)-= 0. n→+ ∞ n n→+∞ n
Soit k ∈ N* .
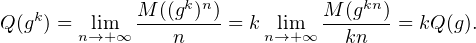
k n kn Q(gk) = lim M-((g-)-)= k lim M-(g--)= kQ (g). n→+∞ n n→+∞ kn
Comme Q(g-k ) = Q((gk)-1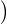) = -Q(gk) on a : Q(g-k) = -Q(gk) = -kQ(g). Finalement : ∀k ∈ Z, Q(gk ) = kQ(g). Ainsi Q est un quasi-caractère.
[Liste des corrigés]

[ < ]