17. Soient G un groupe, δ R, E_δ l’ensemble des applications f de G dans R telles que ∀(x, y) G² , |f(xy) - f(x)f(y)|≤ δ.

a) Montrer que, si f E_δ n’est pas bornée, alors ∀(x,y) G²,f(xy) = f(x)f(y).

b) Trouver C > 0 tel que, pour toute f E_δ, on ait soit ∀x G,|f(x)|≤ C, soit ∀(x, y) G² , f(xy) = f(x)f(y).

a) Soit f E_δ \{0}. Fixons (x,y) G². Soit z G tel que f(z)≠0. Démontrons que

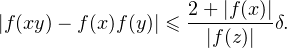(1)

L’appartenance de f à E_δ donne en effet les trois inégalités

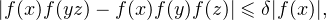
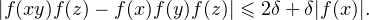
et d’où, par inégalité triangulaire, On obtient alors () en divisant par f(z). À partir de là, si f n’est pas bornée on peut trouver une suite (z_n )_n G^N telle que |f(z_n)| tende vers + ∞ quand n tend vers + ∞, et on obtient alors f(xy) - f(x)f(y) = 0 en passant à la limite dans ().

b) Soit f E_δ bornée. Notons N := ∥f∥_∞. En particulier, pour tout x G, on a |f(x² ) - f(x)² | ≤ δ, donc |f(x)|² ≤ δ + |f(x²)|≤ δ + N, d’où N² ≤ δ + N (passage à la borne supérieure après réécriture |f(x)|≤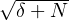). Le trinôme X² - X - δ est de discriminant 1 + 4δ ≥ 0 ; il est donc scindé sur R et sa plus grande racine est

Ainsi, tout élément borné f de E_δ vérifie ∥f∥_∞≤ C. Par contraposition, tout élément f de E_δ non borné par C est, d’après (a), un morphisme de (G,⋅) dans (R,×). Ainsi, tout élément de E_δ est soit borné par C, soit un morphisme de (G,⋅) dans (R,×).

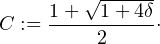
Remarque : en considérant la fonction f : x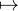C, qui est bien dans E_δ, on voit que la constante C est optimale.

[Liste des corrigés]