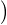13. Pour n  N *, on note g(n) le maximum des ordres des éléments de
N *, on note g(n) le maximum des ordres des éléments de  n. Montrer que
∀k
n. Montrer que
∀k  N * ,
N * , 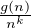
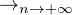 +∞.
+∞.
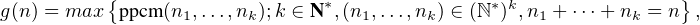
ou
encore
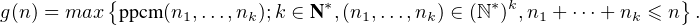
![[ (1- x)axb]1 b ∫ 1 b
J(a,b)= - ----a---- + a- (1 - x)axb-1dx = a-J(a + 1,b- 1).
0 0](/numeros/RMS130-3/RMS130-3450x.png)
On
en déduit par récurrence sur b :
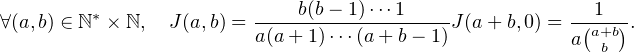
Notons M = ppcm(b + 1,b + 2,…,b + a). Alors, par la formule du binôme :
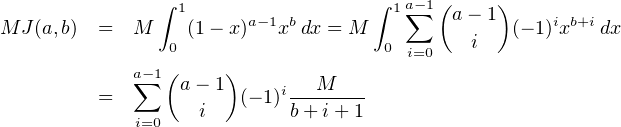
Les 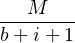 sont tous entiers donc MJ(a,b)
sont tous entiers donc MJ(a,b)  N*, ce qui achève la preuve.
N*, ce qui achève la preuve.
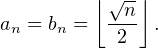
Alors
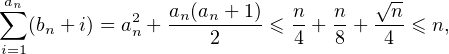
et, en
utilisant le lemme,
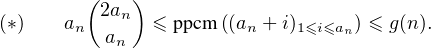
Enfin, d’après la formule de Stirling,
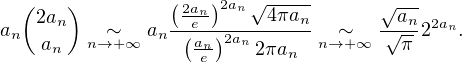
Soit
maintenant k  N *. Alors, par croissance comparée,
N *. Alors, par croissance comparée,
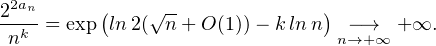
On
déduit de (*) que
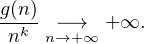
[Liste des corrigés]
 N *, on note g(n) le maximum des ordres des éléments de
N *, on note g(n) le maximum des ordres des éléments de  n. Montrer que
∀k
n. Montrer que
∀k  N * ,
N * , 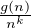
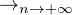 +∞.
+∞.
Solution d’après Ivan Gozard
On sait que chaque élément de  n se décompose en produit de cycles à supports disjoints et ce de
façon unique. Comme l’ordre du produit d’éléments qui commutent entre eux est le ppcm de leurs
ordres respectifs et l’ordre d’un cycle est sa longueur, il vient :
n se décompose en produit de cycles à supports disjoints et ce de
façon unique. Comme l’ordre du produit d’éléments qui commutent entre eux est le ppcm de leurs
ordres respectifs et l’ordre d’un cycle est sa longueur, il vient :
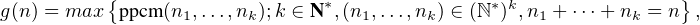
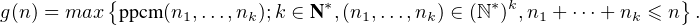
∙ Le lemme suivant est tiré de la réponse 903 pages 113-115, RMS vol. 128 No 4, juillet 2018 :
Preuve : Pour a ≥ 1 et b ≥ 0, posons J(a,b) = 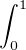 (1 - x)a-1xb d x.
(1 - x)a-1xb d x.
Si b ≥ 1, une intégration par parties donne
![[ (1- x)axb]1 b ∫ 1 b
J(a,b)= - ----a---- + a- (1 - x)axb-1dx = a-J(a + 1,b- 1).
0 0](/numeros/RMS130-3/RMS130-3450x.png)
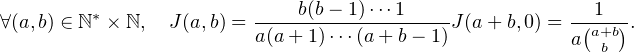
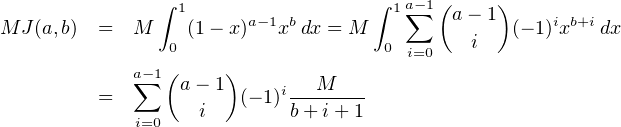
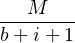 sont tous entiers donc MJ(a,b)
sont tous entiers donc MJ(a,b)  N*, ce qui achève la preuve.
N*, ce qui achève la preuve.
∙ Posons, pour n  N* :
N* :
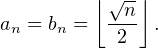
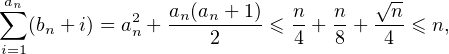
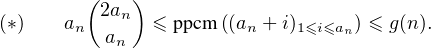
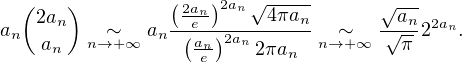
 N *. Alors, par croissance comparée,
N *. Alors, par croissance comparée,
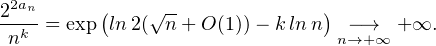
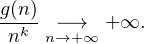
Remarques
- 1.
- Notons (pi )i≥1 la suite des nombres premiers rangés dans l’ordre croissant. Le
théorème des nombres premiers assure que
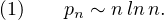
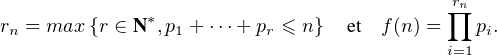
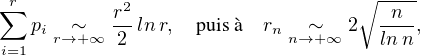
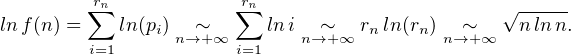
- 2.
- On peut rendre cette démonstration plus élémentaire en remplaçant (1) par les estimations de Tchebychev.
- 3.
- Des calculs plus précis montrent que lng(n) ~
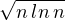 .
.
[Liste des corrigés]