[Table des matières]
Du côté des élèves
de Terminale S
Questions proposées aux élèves de Terminale S
1. Soit8
Mn = 2n - 1 où n  N \
N \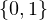 . Montrer que Mn ne peut s’écrire sous la forme Mn = ab où
a
. Montrer que Mn ne peut s’écrire sous la forme Mn = ab où
a  N * et b
N * et b  N \
N \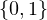 .
.
2. Montrer que pour tout (a,b)  R × R
R × R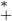 , ab ≤ ea + b
, ab ≤ ea + b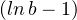 et préciser le cas
d’égalité.
et préciser le cas
d’égalité.
3. Soient ABC un triangle, 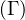 le cercle circonscrit àABC et I,J,K les milieux respectifs de
[BC], [CA] et [AB]. Trois droites de même direction d passant par A,B,C recoupent
le cercle circonscrit àABC et I,J,K les milieux respectifs de
[BC], [CA] et [AB]. Trois droites de même direction d passant par A,B,C recoupent 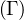 respectivement en Aʹ,Bʹ,Cʹ. Soient Aʹʹ le symétrique de Aʹ par rapport à I, Bʹʹ le symétrique de
Bʹ par rapport à J et Cʹʹ le symétrique de Cʹ par rapport à K.
respectivement en Aʹ,Bʹ,Cʹ. Soient Aʹʹ le symétrique de Aʹ par rapport à I, Bʹʹ le symétrique de
Bʹ par rapport à J et Cʹʹ le symétrique de Cʹ par rapport à K.
Montrer que les trois points Aʹʹ,Bʹʹ,Cʹʹ sont alignés sur une droite perpendiculaire à d passant par l’orthocentre de ABC.
4. Le mélange parfait à l’américaine d’un paquet de 2n cartes consiste à le diviser en deux parties de n cartes puis à placer les cartes de chacune de ces parties alternativement l’une sur l’autre, de sorte que les cartes initialement dans l’ordre 1,2,…,2n forment l’arrangement 1, n + 1, 2, n + 2,…,k,n + k,…,n,2n.
a) On suppose que n ≥ 2. Montrer qu’en effectuant au plus 2(n - 1) mélanges parfaits à l’américaine, on peut retrouver l’ordre initial.
b) Déterminer le nombre minimal de mélanges parfaits à l’américaine permettant de recouvrer l’ordre initial des cartes pour un jeu de 32 cartes ; de 52 cartes.
Olympiade internationale de mathématiques 2019 : corrigé des exercices 2, 4, 5, 6 .
Solutions rédigées par Vincent Jugé.
Exercice 2. Soit A1 et B1 deux points appartenant respectivement aux côtés [BC] et [AC] d’un
triangle ABC. Soit également P et Q deux points appartenant respectivement aux segments [AA1]
et [BB1 ], de sorte que les droites (PQ) et (AB) soient parallèles. Soit P1 un point, situé sur la
droite (PB1 ), tel que B1 se retrouve strictement entre P et P1, et tel que 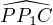 =
= 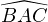 . De
même, soit Q1 un point, situé sur la droite (QA1), tel que A1 se retrouve strictement entre Q et Q1,
et tel que
. De
même, soit Q1 un point, situé sur la droite (QA1), tel que A1 se retrouve strictement entre Q et Q1,
et tel que 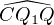 =
= 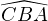 .
.
Démontrer que les points P , Q, P1 et Q1 sont cocycliques.
Solution. Soit Γ le cercle circonscrit à ABC et A2, B2 les points d’intersection respectifs de (AA1 ) et (BB1 ) avec Γ, autres que A et B eux-mêmes.
On constate alors, en utilisant des angles de droites, que
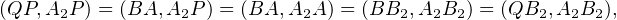
donc que les points P , Q, A2 et B2 sont cocycliques.
De même, puisque
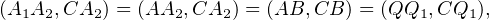
c’est que les points C, A1, A2 et Q1 sont cocycliques. On en déduit alors que
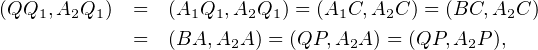
donc que les points P , Q, A2 et Q1 sont eux aussi cocycliques.
Mais alors les points P , Q, A2, B2 et Q1 sont cocycliques. De même, les points P , Q, A2, B2 et P1 sont cocycliques, et les points P , Q, P1 et Q1 sont donc bien cocycliques.
Exercice 4. Trouver tous les couples d’entiers naturels non nuls (k,n) tels que
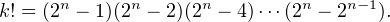
Solution. Pour tout n, on pose
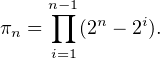
Après avoir constaté que 1! = π1 et que 3! = π2, nous allons démontrer que les couples (1,1) et (3, 2) sont les seules solutions.
Ainsi, soit (k, n) une solution éventuelle. Si n = 1, alors seul k = 1 convient et, si n = 2, seul k = 2 convient. Puis, en remarquant que 5! = 120 < π3 = 168 < 6! = 720 et que 7! = 5040 < π4 = 20160 < 8! = 40320, on constate qu’il n’y a pas d’autres couples solutions que les nôtres, pour n ≤ 4.
On suppose donc désormais que n ≥ 5. La formule de Legendre indique que
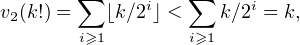
de sorte que
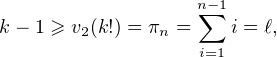
où l’on a posé l = n(n - 1)⁄2.
En remarquant que 5l⁄2 = n(n - 1) + l⁄2 ≥ n(n - 1) + n = n2, on déduit alors que
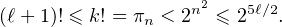
On s’intéresse alors à la fonction f : x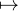 (x + 1)!⁄25x⁄2, car on vient de montrer que f(l) < 1. Or,
pour tout x ≥ 6, on sait que
(x + 1)!⁄25x⁄2, car on vient de montrer que f(l) < 1. Or,
pour tout x ≥ 6, on sait que
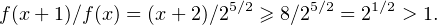
La fonction f est donc strictement croissante sur {6,7,…}. En outre, on peut calculer que
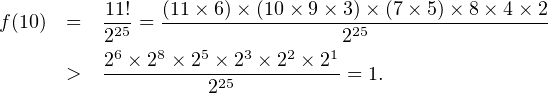
Puisque n ≥ 5, on sait enfin que l = n(n - 1)⁄2 ≥ 10, de sorte que f(l) ≥ f(10) > 1, ce qui constitue la contradiction recherchée.
Les seules solutions sont donc bien les couples (1,1) et (3,2).
Exercice 5. La banque de Bath a émis des pièces dont une face est marquée de la lettre H et l’autre face est marquée de la lettre T . Morgane a aligné n de ces pièces de gauche à droite. Elle réalise alors plusieurs fois de suite l’opération suivante : si la lettre H est visible sur exactement k pièces, avec k ≥ 1, alors Morgane retourne la kème pièce en partant de la gauche ; si k = 0, elle s’arrête. Par exemple, si n = 3, le processus partant de la configuration THT sera
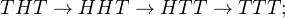
Morgane s’arrête donc au bout de 3 opérations.
- (a)
- Démontrer que, quelle que soit la configuration initiale, Morgane doit s’arrêter au bout d’un nombre fini d’opérations.
- (b)
- Pour chaque configuration initiale C, on note L(C) le nombre d’opérations que va réaliser Morgane avant de s’arrêter. Par exemple, L(THT) = 3 et L(TTT) = 0. Trouver la valeur moyenne des nombres L(C) obtenus lorsque C parcourt l’ensemble des 2n configurations initiales possibles.
Solution. Soit C une configuration donnée : on lui donne un score λ(C) défini comme suit. Tout d’abord, on attribue à la kème pièce de C un score de 2k si cette pièce montre sa face H, et de 0 sinon. Puis on attribue à toute paire (ordonnée) de pièces un score de - 1 si ces deux pièces montrent leur face H, et de 0 sinon. Le score λ(C) est égal à la somme de ces scores individuels.
Regardons maintenant ce qui se passe lorsque, à partir d’une configuration C où k pièces montrent leur face H, Morgane retourne la kème pièce.
- Si la kème pièce montrait sa face T , et montre maintenant sa face H, alors elle contribue pour un score de 2k ; cependant, on vient de former 2k + 1 nouvelles paires de pièces arborant leur face H, et le score λ(C) vient donc de diminuer de 1.
- Si la kème pièce montrait sa face H, et montre maintenant sa face T , alors elle cesse de contribuer pour un score de 2k ; cependant, on vient de détruire 2k - 1 paires de pièces arborant leur face H, et le score λ(C) a donc également diminué de 1.
Dans tous les cas, le score λ(C) décroît de 1 à chaque opération de Morgane. Puisque λ(C) ≥-n2 pour toute configuration C, Morgane doit donc nécessairement s’arrêter au bout d’un nombre fini d’opérations. ce moment-là, elle a obtenu la configuration TT…T , de score nul. Par conséquent, Morgane a donc dû effectuer λ(C) opérations avant de s’arrêter, ce qui montre que L(C) = λ(C).
On calcule maintenant la valeur moyenne que prend λ(C) quand C décrit l’ensemble des 2n configurations. Pour tout k, la kème pièce apporte un score de 2k dans la moitié des cas, soit un score moyen de k. Puis toute paire formée de 2 pièces distinctes apporte un score de - 1 dans un quart des cas, soit un score moyen de - 1⁄4 ; il y a n(n- 1) telles paires. Enfin, toute paire formée de 2 fois la même pièce apporte un score de - 1 dans la moitié des cas, soit un score moyen de - 1⁄2 ; il y a n telles paires.
La valeur moyenne de λ(C), c’est-à-dire de L(C), vaut donc
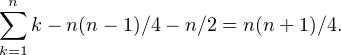
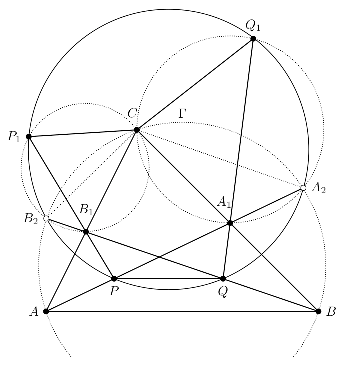
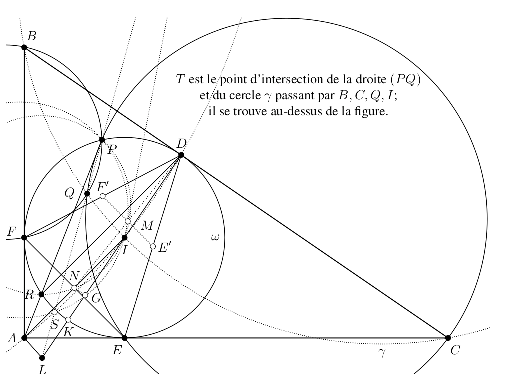
Exercice 6. Soit ABC un triangle dont tous les angles sont aigus et tel que AB≠AC. On note ω le cercle inscrit dans ABC, I le centre de ω, et D, E et F les points de contact respectifs de ω avec les côtés [BC], [CA] et [AB]. Soit R le point de ω, autre que D, tel que la droite (DR) soit perpendiculaire à (EF). Soit P le point d’intersection, autre que R, entre la droite (AR) et le cercle ω. Enfin, soit Q le point d’intersection, autre que P , entre les cercles circonscrits à PCE et à PBF.
Démontrer que les droites (DI) et (PQ) sont sécantes en un point appartenant à la perpendiculaire à (AI) passant par A.
Solution. Soit L le point d’intersection de (DI) et de la perpendiculaire à (AI) passant par A. Dans la suite, nous allons démontrer que P , Q et L sont alignés.
Soit K le point d’intersection de (DI) et de ω, autre que D : il s’agit du point de ω diamétralement opposé à D. Alors (KR) est perpendiculaire à (DR), c’est-à-dire parallèle à (EF), ou encore perpendiculaire à (AI). Ainsi, (AI) est une hauteur du triangle KIR, et puisque KI = RI, c’est la médiatrice de [KR].
Maintenant, soit N le milieu du segment [EF]. Puisque (AI) est la médiatrice de [EF], elle contient N, et les triangles ANE et AEI sont respectivement rectangles en N et en E. Ils sont donc semblables, de sorte que
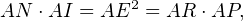
et donc que les points N, I, R et P sont cocycliques.
Puisque IR = IP , le théorème du pôle Sud, appliqué au cercle circonscrit à N, I, R et P , indique
alors que (NI) est une bissectrice (ici, extérieure) de l’angle 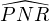 . Or, c’est également la
bissectrice intérieure de
. Or, c’est également la
bissectrice intérieure de 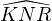 . Les points K, N et P sont donc alignés.
. Les points K, N et P sont donc alignés.
Soit ensuite S le point d’intersection de (DN) et de ω autre que D, et soit G le projeté orthogonal de N sur la droite (KD). Puisque
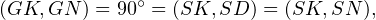
les points G, K, S et N sont cocycliques, car ils appartiennent au cercle de diamètre [KN].
Mais alors, en vertu du théorème de l’angle au centre,
| (IG, IP) | = (ID,IP) = 2(KD,KP) = (KD,KP) + (SD,SP) | ||
| = (KG,KN) + (SN,SP) = (SG,SN) + (SN,SP) = (SG,SP), |
de sorte que I, G, S et P sont cocycliques.
En outre, les triangles IGN et IAL sont respectivement rectangles en G et en A. Ils sont donc semblables. De même, les triangles INE et ANE sont rectangles en N, donc ils sont tous deux semblables à AEI. On en déduit que
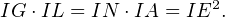
Par conséquent, l’inversion de centre I et de rapport IE2 envoie P et S sur eux-mêmes, et envoie G sur L. Puisqu’elle envoie le cercle circonscrit à I, G, S et P sur une droite, les points P , S et L sont donc alignés. Il ne nous reste donc plus qu’à prouver que P , Q et S sont eux aussi alignés.
Or, puisque (BF) et (EC) sont des tangentes à ω, on sait que
| (QB, QC) | = (QB,QP) + (QP + QC) = (FB,FP) + (EP,EC) | ||
| = (EF,EP) + (FP,FE) = (PF,PE) | |||
| = (DF,DE) = (DF,BI) + (BI,CI) + (CI,DE) | |||
| = 90• + (BI,CI) + 90• = (IB,IC). |
Cela signifie que les points B, C, Q et I sont cocycliques : soit γ leur cercle circonscrit.
Soit alors T le point d’intersection de (PQ) et de γ autre que Q : il nous suffit en fait de prouver que P, S et T sont alignés.
Or, puisque [KD] est un diamètre de ω, on sait que (FK) est perpendiculaire à (FD), c’est-à-dire parallèle à (BI). Ainsi, toujours puisque (BF) est tangente à ω, on en déduit que
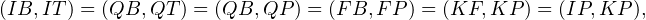
de sorte que (IT) se retrouve parallèle à (KP), ou encore à (KN). Et, comme I est le milieu de [KD], la droite (IT) est donc une droite des milieux du triangle NKD, et elle contient donc le milieu de [DN], que l’on notera M.
Enfin, soit Eʹ et Fʹ les milieux respectifs de [DE] et de [DF]. Notons que Eʹ est le point d’intersection de (DE) et de (CI). Or, puisque les triangles CDI et CEI sont rectangles en D et en E, les points C, D, I et E appartiennent à un même cercle γʹ. Mais alors Eʹ a même puissance par rapport à ω, γʹ et γ. De même, Fʹ a même puissance par rapport à ω et à γ, et la droite (EʹFʹ) est donc l’axe radical de ces deux cercles.
Puisque c’est une droite des milieux de DEF , elle passe également par le milieu M de la médiane [DN], donc M a même puissance par rapport à ω et à γ. On en déduit que
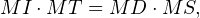
donc que les points D, I, S et T sont cocycliques. Mais alors
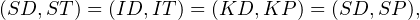
ce qui conclut.
[Table des matières]

