[Questions-Reponses]
R917. Soit a un entier strictement positif. On note Ua le polynôme X4 -aX - 1. On note α la racine réelle positive de Ua.
Quelles sont les valeurs de a pour lesquelles α est constructible à la règle et au compas ? (Alain Tissier)
Réponse composée de celles de Guy Alarcon, Alain Rémondière et Alain Tissier
On montrera que si une des racines de Ua est constructible à la règle et au compas alors a = 4.
Réciproquement les racines du polynôme X4 - 4X - 1 sont constructibles à la règle
et au compas ; ce sont ε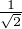 + εʹ
+ εʹ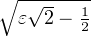 où ε et εʹ prennent les valeurs 1 ou - 1.
où ε et εʹ prennent les valeurs 1 ou - 1.
L’étude des variations de Ua montre que ses racines sont distinctes ; ce sont deux réels
α et β tels que - 1 < β < 0 < 1 < α et des complexes conjugués non réels ω et ω.
On suppose que l’une des racines, z, de Ua est constructible à la règle et au compas. On montre d’abord qu’il existe un entier positif n tel que
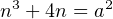 | (1) |
On utilise une propriété classique des polynômes unitaires non constants à coefficients entiers. Soit
P un tel polynôme ; tout polynôme unitaire à coefficients rationnels divisant P dans
Q[X] est à coefficients entiers. Ainsi P est irréductible dans Q[X] si et seulement si il
n’existe pas deux polynômes unitaires à coefficients entiers non constants dont P est le
produit.
Montrons d’abord que Ua est irréductible dans Q[X]. Comme Ua est unitaire à coefficients entiers,
il suffit de prouver qu’il n’existe pas A et B unitaires non constants à coefficients entiers tels que
AB = Ua .
⊳ Supposons Ua = (X + t)(X3 + uX2 + vX + w) où t,u,v,w sont entiers, alors tw = 1 ;
t = ±1 ; ceci impose 1 ou - 1 comme racine de Ua, ce qui n’est pas.
⊳ Supposons Ua = (X2 + tX + u)(X2 + vX + w) où t,u,v,w sont entiers, alors v = -t ;
uw = -1 donc u = ±1 et w = -u ; w + u + tv = 0 donc t2 = 0 et t = 0 ; finalement
Ua = X4 - 1, ce qui n’est pas puisque a n’est pas nul.
Soit des corps K1 ,K2,K3 tels que K1 ⊂ K2 ⊂ K3 ; on note classiquement (K2 : K1) la dimension de K2 en tant qu’espace vectoriel sur K1. On utilisera plusieurs fois :
(K3 : K1 ) = (K3 : K2)(K2 : K1).
Comme Ua est irréductible sur Q, il est le polynôme minimal de z sur Q, donc le corps Q(z)
vérifie : (Q (z) : Q) = 4. Comme z est constructible à la règle et au compas, il existe
une chaîne croissante de sous-corps de C : K0 = Q ⊂ K1 ⊂ K2 ⊂ ⊂ Km telle
que
⊂ Km telle
que
z  Km ; ∙ z
Km ; ∙ z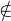 Km-1 ; ∙(Kj : Kj-1) = 2 pour j = 1,2,….
Km-1 ; ∙(Kj : Kj-1) = 2 pour j = 1,2,….
Par récurrence facile (Kj : Q) = 2j.
Nécessairement Km = Km-1(z). Le polynôme minimal unitaire V de z sur Km-1 est un diviseur
de Ua dans Km-1 et il est de degré deux. Donc V = X2 + tX + u où t et u sont des éléments
de Km-1 . Dans Km-1[X], Ua se décompose : Ua = V W où, après identification,
W = X2 - tX -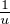 .
.
De plus :
u - 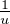 = t2 ; t
= t2 ; t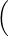 u +
u + 
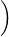 = a,
= a,
on en tire :
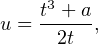
puis :
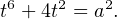
Les formules précédentes montrent que V est à coefficients dans le corps Q(t). De plus z n’est pas
dans Km-1 ; V est donc le polynôme minimal de z sur Q(t).
Le polynôme minimal unitaire de t sur Q est un diviseur Q de P = X6 + 4X2 -a2. Le degré de Q est (Q (t) : Q ). D’autre part Q(t) est un sous-corps de Km-1 ; comme
(Km-1 : Q (t))(Q(t) : Q) = 2m-1,
(Q (t) : Q ) est une puissance de 2 au plus égale à 6. Le degré de Q est donc 1, 2 ou 4. Donc P est
réductible sur Q .
Montrons d’abord que P n’a aucune racine entière. Raisonnons par l’absurde. Soit un entier b tel
que P(b) = 0 ; clairement b n’est pas nul et comme b est pair, on peut supposer b > 0. Alors
(b4 + 4)b2 = a2 ; donc b divise a ; ainsi a = bc où c  N* ; puis
N* ; puis
c2 - b4 = 4, (c + b2)(c - b2) = 4, c + b2 = 4 et c - b2 = 1, 2b2 = 3 : impossible.
Ainsi P n’a aucun facteur irréductible de degré un.
Si Q est de degré quatre alors le quotient de P par Q est un facteur irréductible de degré deux. Donc
P possède un facteur irréductible R de degré deux, R = X2 + bX + c où b et c sont entiers. Si
b = 0 alors l’entier n = -c vérifie (). Sinon R(-X) = X2 - bX + c est un autre facteur
irréductible de P (puisque P est pair) et P(X) = R(X)R(-X)S(X) où S(X) = X2 + d, d entier.
L’entier n = -d vérifie ().
On vient d’établir que si l’une des racines de Ua est constructible alors il existe un entier n vérifiant
().
Montrons à présent que () ne peut être satisfaite que si a = 4, n étant alors égal à 2.
Soit n un entier vérifiant (). D’abord n n’est pas un carré car on a vu que P n’a pas de racine
entière. Le PGCD de n et de n2 + 4 est 1, 2 ou 4.
⊳ Si ce PGCD est 1 alors n et n2 + 4 sont premiers entre eux et leur produit est un carré, donc ce sont tous deux des carrés ; impossible car n n’est pas un carré.
⊳ Si ce PGCD est 4 alors n = 4nʹ pour un certain entier nʹ > 0 et a = 4aʹ pour un certain aʹ > 0 ;
puis nʹ(1 + 4nʹ2 ) = aʹ2 ; nʹ et 1 + 4nʹ2 sont premiers entre eux ; nʹ est un carré et n aussi ;
impossible.
Donc le PGCD de n et de n2 + 4 est 2. Il en résulte que n = 2q où q est un entier impair et que a = 4b où b est entier. L’équation () devient :
q(q2 + 1) = 2b2 .
Les entiers q et (q2 + 1)⁄2 sont premiers entre eux et sont des carrés :
q = r2 ; q2 + 1 = 2s2 ; b = rs.
Finalement il existe des entiers r et s tels que
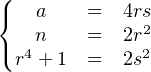
On va montrer à présent que l’équation
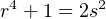 | (2) |
n’a pas d’autre solution dans N2 que r = 1 et s = 1. Si (r,s) est solution de () alors
(r4 - 1)2 = 4(s4 - r4)
donc (r4 - 1)2 est pair. Posons t = 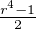 ; alors t, r et s vérifient
; alors t, r et s vérifient
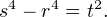 | (3) |
La preuve sera complète quand on aura montré que () n’est satisfaite par aucun triplet d’entiers
naturels tous non nuls.
On raisonne par l’absurde en considérant une solution (s,r,t) telle que s est minimal ; nécessairement (s,r,t) sont deux à deux premiers entre eux. On a : (r2)2 + t2 = (s2)2 ; ainsi (r2 , t, s2 ) est un triangle pythagoricien.
- 1.
- si r est pair (donc t est impair). On sait qu’il existe u,v
 N*, u pair et v impair tels
que
N*, u pair et v impair tels
que
u ∧ v = 1 et r2 = 2uv, t = ε(u2 - v2), s2 = u2 + v2, où ε = ±1.
Comme s2 = u2 + v2, il existe x,y
 N* de parités différentes tels que x ∧ y = 1 et
u = 2xy, v = x2 - y2, s = x2 + y2. Alors
N* de parités différentes tels que x ∧ y = 1 et
u = 2xy, v = x2 - y2, s = x2 + y2. Alors
r2 = 2uv = 4xy(x2 - y2), donc
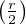 2 = xy(x2 - y2).
2 = xy(x2 - y2).Comme x et y sont premiers entre eux, x∧ (x2 -y2) = 1 et y ∧ (x2 -y2) = 1, donc x,y et x2 - y2 sont des carrés parfaits. Il existe donc λ,μ,ν
 N* tels que :
N* tels que :
x = λ2 , y = μ2 et x2 - y2 = ν2.
Alors ν2 = λ4 - μ4. Le triplet (μ,λ,ν)

 3 est solution de (). De plus on a
λ4 = x2 < x2 + y2 = s ≤ s4, d’où λ < s , ce qui contredit le caractère minimal de
s.
3 est solution de (). De plus on a
λ4 = x2 < x2 + y2 = s ≤ s4, d’où λ < s , ce qui contredit le caractère minimal de
s.
- 2.
- si r est impair (donc t est pair). Il existe u,v
 N* tels que : r2 = u2 - v2 , t = 2uv et
s2 = u2 + v2. Alors
N* tels que : r2 = u2 - v2 , t = 2uv et
s2 = u2 + v2. Alors 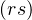 2 = u4 - v4. Le triplet (v,u,rs)
2 = u4 - v4. Le triplet (v,u,rs) 
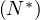 3 est une solution de ()
vérifiant u2 < u2 + v2 = s2, donc u < s, ce qui contredit le caractère minimal de
v.
3 est une solution de ()
vérifiant u2 < u2 + v2 = s2, donc u < s, ce qui contredit le caractère minimal de
v.
[Questions-Reponses]

