[Questions-Reponses]
R828. Posé dans RMS 124-3.
Soit a > 0. On note E l’espace des fonctions réelles f définies sur [0,1], de classe 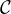 2 et telles
que f(0) = 1 et que f(1) = 0. Pour tout élément f de E, on pose
2 et telles
que f(0) = 1 et que f(1) = 0. Pour tout élément f de E, on pose
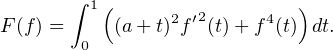
Dans l’exercice précité, on a prouvé la stricte convexité de F , ce qui permet d’affirmer l’unicité d’une fonction minimisant F . De plus, il a été établi que ψ minimise F si et seulement si ψ est une solution sur [0,1] de
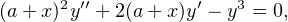
telle que y(0) = 1 et y(1) = 0.
tudier l’existence de cette fonction ψ minimisante. (Alain Tissier)
La référence de l’exercice précité a été oubliée dans l’énoncé. Il s’agit de l’exercice d’oral 103 corrigé dans RMS 122-4. D’autre part l’écriture de l’équation différentielle en question comporte une erreur sur le dernier terme. Voici la bonne :
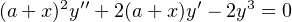 | (1) |
Réponse d’Alain Rémondière
On ne reprendra pas la question de l’unicité, qui se déduit (voir l’exercice mentionné) de la stricte convexité de F.
On note, pour tout k de N, Ck l’espace vectoriel 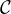 k([0,1], R). On note C
k([0,1], R). On note C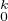 (resp. C
(resp. C ) le
sous-espace vectoriel (resp. affine) de Ck donné par les relations f(0) = f(1) = 0 (resp.
f(0) = 1 et f(1) = 0). L’espace affine C
) le
sous-espace vectoriel (resp. affine) de Ck donné par les relations f(0) = f(1) = 0 (resp.
f(0) = 1 et f(1) = 0). L’espace affine C a pour direction C
a pour direction C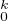 et passe par f0 : t
et passe par f0 : t 1 - t .
1 - t .
On munit l’espace C0 est muni de la norme ∥⋅∥∞, et l’espace C1 du produit scalaire donné par :
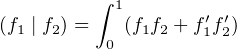 | (2) |
On veut minimiser sur C la fonctionnelle F : C1 → R donnée par
la fonctionnelle F : C1 → R donnée par
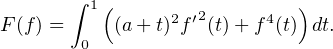
Mais C1 n’est pas complet pour la norme associée à ce produit scalaire ; ceci crée une difficulté
dans la preuve de l’existence de ce minimum.
Nous allons étendre la définition de F au complété de C1 (on le notera H1) que l’on va décrire ci-après : de manière informelle, il s’agit des fonctions continues sur [0,1] ayant une dérivée de carré intégrable, en un sens faible.
On note L2 l’espace de Hilbert des fonctions de [0,1] dans R de carré intégrable muni de la norme
∥⋅ ∥2 (selon l’usage, on identifie une classe et l’un des ses représentants).
On note, pour tout k de N, Dk le sous-espace vectoriel de C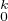 constitué des fonctions f
de classe
constitué des fonctions f
de classe 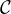 k à support compact inclus dans ]0,1[ ; on sait que D1 est dense dans L2.
k à support compact inclus dans ]0,1[ ; on sait que D1 est dense dans L2.
Proposition 1.Soit g un élément de L2. On note f : [0,1] → R la fonction x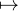
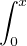 g(t)d t.
Alors :
g(t)d t.
Alors :
a) f est définie sur [0,1], continue et même 1⁄2-holdérienne.
b) Elle vérifie :
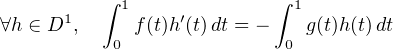 | (3) |
Démonstration.a) Le résultat provient de l’inégalité de Cauchy-Schwarz :
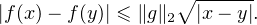
b) On transforme l’intégrale 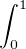 gh en utilisant la règle de Fubini (l’intégration par parties
est interdite ici) :
gh en utilisant la règle de Fubini (l’intégration par parties
est interdite ici) :
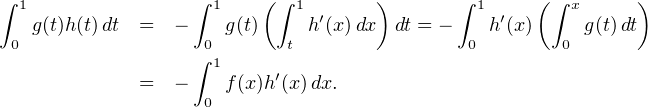
Lemme 1.Soit f dans L2 telle que 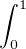 f(t)hʹ(t)d t = 0 pour tout h de D1. Alors f est
presque partout égale à une certaine constante.
f(t)hʹ(t)d t = 0 pour tout h de D1. Alors f est
presque partout égale à une certaine constante.
Démonstration.On vérifie sans mal que h hʹ est une bijection de D1 sur D0 ∩Kerφ, où φ est la
forme linéaire g
hʹ est une bijection de D1 sur D0 ∩Kerφ, où φ est la
forme linéaire g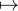
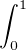 g. Soit K =
g. Soit K = 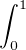 f. Alors pour tout h
f. Alors pour tout h  D0,
D0,
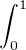 fh =
fh = 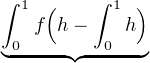 =0 + K
=0 + K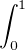 h, donc
h, donc 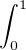 (f - K)h = 0.
(f - K)h = 0.
On en déduit que f - K est nulle presque partout. __
En utilisant le lemme et la proposition on établit la proposition suivante.
Soit f dans L2 telle qu’il existe g dans L2 vérifiant (). On note 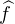 la fonction x
la fonction x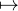 f(x) -
f(x) -
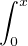 g(t) d t. Alors
g(t) d t. Alors 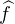 vérifie les hypothèses du lemme . D’après la proposition , f est donc
égale presque partout à une constante.
vérifie les hypothèses du lemme . D’après la proposition , f est donc
égale presque partout à une constante.
Ainsi :
- f est continue (plus exactement f est égale presque partout à une fonction continue à laquelle on l’identifie) ;
- g est déterminée par f.
- f(x) = f(0) +
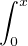 g(t)d t pour tout x de [0,1]
g(t)d t pour tout x de [0,1]
- Si en plus g est dans C0, f est dans C1 et g est sa dérivée au sens ordinaire.
Par définition on appelle dérivée faible de f et on note fʹ la fonction g de la proposition .
On note H1 l’ensemble des fonctions continues de [0,1] dans R ayant une dérivée faible dans L2,
c’est-à-dire vérifiant les hypothèses de la proposition . C’est un sous-espace vectoriel de C0
incluant C1 .
Comme pour les Ck on note H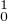 (resp. H
(resp. H ) le sous-espace vectoriel (resp. affine) de H1 donné par
les relations f(0) = f(1) = 0 (resp. f(0) = 1 et f(1) = 0).
) le sous-espace vectoriel (resp. affine) de H1 donné par
les relations f(0) = f(1) = 0 (resp. f(0) = 1 et f(1) = 0).
Pour tous f1 et f2 de H1 on note (f1∣f2) = 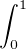 (f1f2 + fʹ1fʹ2) On vérifie aisément que l’on
définit un produit scalaire sur H1 qui prolonge celui de C1. On note simplement ∥⋅∥ la norme
associée.
(f1f2 + fʹ1fʹ2) On vérifie aisément que l’on
définit un produit scalaire sur H1 qui prolonge celui de C1. On note simplement ∥⋅∥ la norme
associée.
a) Pour toute f de H1, on a ∥f∥∞≤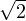 ∥f∥. Ainsi l’injection canonique de (H1,∥⋅∥) dans
(C0 , ∥⋅ ∥∞ ) est continue.
∥f∥. Ainsi l’injection canonique de (H1,∥⋅∥) dans
(C0 , ∥⋅ ∥∞ ) est continue.
b) H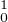 et H
et H sont des fermés de H1.
sont des fermés de H1.
c) Sur H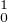 , la restriction de f
, la restriction de f ∥fʹ∥2 est une norme équivalente à la restriction de ∥⋅∥.
∥fʹ∥2 est une norme équivalente à la restriction de ∥⋅∥.
d) L’injection canonique de (H1,∥⋅∥) dans (C0,∥⋅∥∞) est compacte.
Démonstration.a) On a, pour tous x,y de [0,1] :
|f(x) - f(y)| ≤ 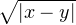
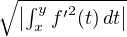 ≤∥fʹ∥2.
≤∥fʹ∥2.
Donc |f(x)| ≤ |f(y)| + ∥fʹ∥2. Intégrons cette inégalité par rapport à y :
|f(x)| ≤ 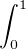 |f(y)|d y + ∥fʹ∥2.
|f(y)|d y + ∥fʹ∥2.
Mais 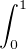 |f(y)|d y ≤∥f∥2. Donc |f(x)|≤∥f∥2 + ∥fʹ∥2 ≤
|f(y)|d y ≤∥f∥2. Donc |f(x)|≤∥f∥2 + ∥fʹ∥2 ≤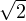 ∥f∥. C’est vrai pour tout x de [0,1],
donc ∥f∥∞ ≤
∥f∥. C’est vrai pour tout x de [0,1],
donc ∥f∥∞ ≤ 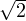 ∥f∥.
∥f∥.
b) Pour tout a de [0,1] et toute f de H1, on a |f(a)|≤∥f∥∞≤∥f∥. Donc l’évaluation en a est une
forme linéaire continue sur H1. Il en résulte que, d’après leur définition, H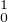 et H
et H sont des fermés
de H1 .
sont des fermés
de H1 .
c) Soit f un élément de H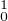 . On a évidemment ∥fʹ∥2 ≤∥f∥. Pour tout x de [0,1] on
a
. On a évidemment ∥fʹ∥2 ≤∥f∥. Pour tout x de [0,1] on
a
f2 (x) ≤ x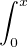 fʹ2(t)d t ≤ x∥fʹ∥
fʹ2(t)d t ≤ x∥fʹ∥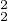 .
.
Puis par intégration : ∥f∥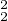 ≤
≤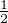 ∥fʹ∥
∥fʹ∥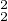 ; enfin ∥f∥2 ≤
; enfin ∥f∥2 ≤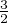 ∥fʹ∥
∥fʹ∥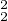 ; donc ∥f∥≤
; donc ∥f∥≤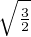 ∥fʹ∥2. La preuve
est complète.
∥fʹ∥2. La preuve
est complète.
d) Soit (fn ) une suite bornée de H1. Soit M un majorant commun à toutes les ∥fn∥. On a pour tout
n et tous x, y de [0,1], |fn(x) - fn(y)|≤ M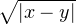 . Cette majoration uniforme permet
d’appliquer le théorème d’Ascoli qui donne le résultat voulu. __
. Cette majoration uniforme permet
d’appliquer le théorème d’Ascoli qui donne le résultat voulu. __
Démonstration.Soit (fn) une suite de Cauchy dans H1. D’après la définition de ∥.∥, (fʹn)
est une suite de Cauchy dans L2. Comme L2 est complet, la suite (fʹn) converge dans L2
vers une fonction g.
D’après la proposition la suite (fn) est de Cauchy au sens de la norme uniforme, et elle converge uniformément vers une fonction f continue.
On a, pour tout x, 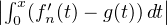 ≤∥fʹn - g∥2, donc
≤∥fʹn - g∥2, donc
fn (x) = fn (0) + 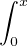 fʹn(t)d t tend vers f(x) = f(0) +
fʹn(t)d t tend vers f(x) = f(0) + 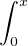 g(t)d t.
g(t)d t.
Ainsi, d’après les propositions et , f est dans H1 et g est la dérivée faible de f. De plus ∥f - fn∥2 tend vers 0 puisque ∥f - fn∥2 ≤∥f - fn∥∞ et ∥fʹ- fnʹ∥2 tend vers 0 ; donc ∥f - fn∥ tend vers 0. __
Ainsi H1 et H sont des espaces de Hilbert.
sont des espaces de Hilbert.
Démonstration.
a) Soit f dans H1 . Notons g sa dérivée faible ; g est dans L2. Il existe dans C une suite (gn) qui
converge vers g dans L2. On définit alors (fn) par
une suite (gn) qui
converge vers g dans L2. On définit alors (fn) par
fn (x) = f(0) + 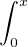 gn(t)d t.
gn(t)d t.
Les fn sont dans C1 et convergent vers f dans H1 puisque (fʹn) converge vers g dans L2 et (fn)
converge vers f pour ∥⋅∥∞ donc pour ∥⋅∥2.
b) Q [X] est dense dans C0 pour ∥⋅∥∞ d’après le théorème de Weierstrass et la densité de Q dans R. En reprenant les notations de a), on peut trouver Pn dans Q[X] tel que
∥gn - Pn ∥2 ≤ ∥gn - Pn∥∞≤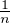 ⋅
⋅
En posant Qn (x) = an + 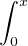 Pn(t)d t, où (an) est une suite de rationnels qui tend vers f(0), on
construit une suite de polynômes à coefficients rationnels qui converge vers f dans H1 (même
raisonnement qu’au a). Et Q[X] est dénombrable. __
Pn(t)d t, où (an) est une suite de rationnels qui tend vers f(0), on
construit une suite de polynômes à coefficients rationnels qui converge vers f dans H1 (même
raisonnement qu’au a). Et Q[X] est dénombrable. __
On étend à H1 la définition de F . On établira l’existence et l’unicité d’une fonction ψ minimisant
F sur H1 . On vérifiera que cette fonction est un élément de C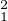 et est solution de () ; donc,
finalement, elle est
et est solution de () ; donc,
finalement, elle est 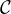 ∞.
∞.
Donnons l’idée générale de la méthode avant de détailler.
On considère une base hilbertienne (ei)i N de H
N de H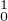 . On pose
. On pose
En = V ect (e0 , e1…en) et Wn = f0 + En
où f0 est la fonction x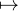 1 -x. On prend un élément fn qui minimise F sur Wn (son existence est
due à un argument de compacité en dimension finie).
1 -x. On prend un élément fn qui minimise F sur Wn (son existence est
due à un argument de compacité en dimension finie).
On prouve alors que (fn) possède une suite extraite de Cauchy dans H1 ; cette suite extraite converge donc dans H1. On vérifie que sa limite ψ vérifie les propriétés indiquées plus haut.
Dans H1 on note B1(R) la boule fermée de centre 0 et de rayon R.
Soit f dans H1 , h dans H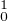 , il vient :
, il vient :
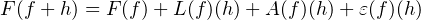 | (4) |
où
- L(f)(h) =
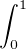
 2(a + t)2fʹ(t)hʹ(t) + 4h(t)f3(t)
2(a + t)2fʹ(t)hʹ(t) + 4h(t)f3(t)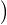 d t ;
d t ;
- A(f)(h) =
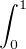 (a + t)2hʹ2(t) + 6h2(t)f2(t)d t ;
(a + t)2hʹ2(t) + 6h2(t)f2(t)d t ;
- ε(f)(h) =
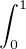 4h3(t)f(t) + h4(t)d t.
4h3(t)f(t) + h4(t)d t.
Lemme 2.a) Pour f fixée il existe K1 telle que |L(f)(h)|≤ K1∥h∥. Ainsi la forme linéaire
L(f) sur H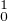 est continue.
est continue.
b) il existe K2 telle que |A(f)(h) + ε(f)(h)|≤ K2∥h∥2 pour toute h de B1(1) ∩ H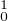 .
.
Démonstration.a) On a :
|L(f)(h)| ≤ 2(a + 1)2∥fʹ∥2∥hʹ∥2 + 4∥f3∥2∥h∥2 ≤ (2(a + 1)2∥fʹ∥2 + 4∥f3∥2∥h∥.
b) D’abord
0 ≤ A(f)(h) ≤ (a + 1)2∥hʹ∥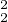 + 6∥f∥
+ 6∥f∥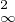 ∥h∥
∥h∥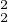 ≤ max((a + 1)2,6∥f∥
≤ max((a + 1)2,6∥f∥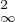 )∥h∥2.
)∥h∥2.
Puis :
|ε(f)(h)| ≤ 4∥h∥∞∥f∥∞∥h∥2 + ∥h∥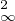 ∥h∥2,
∥h∥2,
et comme ∥h∥∞ ≤∥h∥≤ 1 il vient |ε(f)(h)|≤ 4∥f∥∞ + 1
4∥f∥∞ + 1 ∥h∥2. On obtient ce qu’il faut en
combinant ces deux inégalités. __
∥h∥2. On obtient ce qu’il faut en
combinant ces deux inégalités. __
On en déduit :
Proposition 6.Pour f fixée dans H1, l’application de H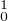 dans R, h
dans R, h F(f+h) est continue
et différentiable en 0 de différentielle L(f). Notamment F est continue sur H
F(f+h) est continue
et différentiable en 0 de différentielle L(f). Notamment F est continue sur H .
.
Voici des inégalités utiles :
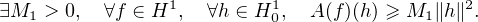 | (5) |
En effet |A(f)(h) ≥ a2∥hʹ∥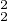 , et on utilise la proposition c).
, et on utilise la proposition c).
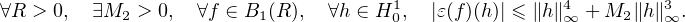 | (6) |
En effet : 
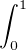 4h3(t)f(t) + h4(t)d t
4h3(t)f(t) + h4(t)d t ≤ 4∥f∥∞∥h∥
≤ 4∥f∥∞∥h∥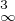 + ∥h∥
+ ∥h∥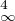 .
.
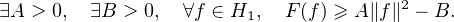 | (7) |
En effet F(f) ≥ a2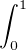 fʹ2 +
fʹ2 + 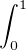 f4. Puisque f4 +
f4. Puisque f4 + 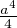 ≥ a2f2, il vient
≥ a2f2, il vient
F(f) ≥ a2 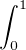 (fʹ2 + f2) -
(fʹ2 + f2) -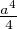 = A∥f∥2 - B avec A = a2 et B =
= A∥f∥2 - B avec A = a2 et B = 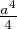 ⋅
⋅
Construction de la suite (fn)n≥1
D’après l’inégalité ineg3, F(f) tend vers + ∞ avec ∥f∥. Sur Wn qui est un sous-espace
affine de dimension finie, par continuité de F , la restriction de F admet un minimum
mn atteint en un point fn. Par définition, (mn) est une suite décroissante positive, elle
converge.
Toujours grâce à l’inégalité (), la suite (∥fn∥) est majorée disons par R > 0.
Pour tout n, l’application de Fn dans R, h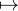 F(fn + h) est différentiable en 0, sa différentielle en
0 est h
F(fn + h) est différentiable en 0, sa différentielle en
0 est h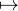 L(fn )(h) et cette différentielle est nulle puisque F(fn + h) ≥ F(fn) pour tout h de
En .
L(fn )(h) et cette différentielle est nulle puisque F(fn + h) ≥ F(fn) pour tout h de
En .
D’après la proposition d), comme (fn) est bornée dans H1 il existe une partie infinie P de
Ntelle que la sous-suite (fn)n P converge selon ∥⋅∥∞. Pour p > n > 0, n,p
P converge selon ∥⋅∥∞. Pour p > n > 0, n,p  P , il
vient :
P , il
vient :
F(fn ) = F(fp ) + A(fp)(fn - fp) + ε(fp)(fn - fp)
(la partie linéaire est nulle puisque fn - fp est dans Ep).
En appliquant les inégalités ineg1 et ineg2 avec R défini ci-dessus, il vient :
mn - mp ≥ M1 ∥fn - fp∥2 -∥fn - fp∥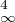 - M2∥fn - fp∥
- M2∥fn - fp∥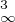 .
.
La suite (fn )n P converge pour ∥⋅∥∞ et la suite (mn)n
P converge pour ∥⋅∥∞ et la suite (mn)n P converge dans R ; on en déduit que
(fn )n
P converge dans R ; on en déduit que
(fn )n P est de Cauchy dans H1. Par complétude de H1 elle converge dans H1 vers un élément
noté ψ.
P est de Cauchy dans H1. Par complétude de H1 elle converge dans H1 vers un élément
noté ψ.
D’abord ψ est dans H qui est fermé.
qui est fermé.
Par définition de (fn), F(fn + h) ≥ F(fn) pour tout h de En. Soit n0 dans P . On fixe h dans
En0 . On écrit cette inégalité pour n ≥ n0, n  P . Comme F est continue, par passage à la
limite,
P . Comme F est continue, par passage à la
limite,
F(ψ + h) ≥ F(ψ).
Comme c’est vrai pour tout n0 de P et que la réunion des Fn0 est dense dans H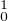 , l’inégalité
précédente est vraie pour toute h de H
, l’inégalité
précédente est vraie pour toute h de H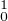 . Ainsi, ψ réalise le minimum de F sur H
. Ainsi, ψ réalise le minimum de F sur H .
.
La différentielle de F en ψ est nulle et L(ψ)(h) = 0 pour tout h de H , i.e
, i.e
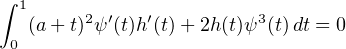 | (8) |
D’après la proposition , cela veut dire que φ : t (a + t)2ψʹ(t) est dans H1 et que sa
dérivée faible est 2ψ3 qui est continue, donc φ est
(a + t)2ψʹ(t) est dans H1 et que sa
dérivée faible est 2ψ3 qui est continue, donc φ est 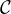 1 puis ψ est
1 puis ψ est 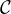 2 et vérifie l’équation
ED.
2 et vérifie l’équation
ED.
Cette équation différentielle satisfaite par ψ montre à son tour que ψ est en fait 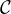 ∞.
∞.
1) La fin de la démonstration montre que la seule valeur d’adhérence de (fn) dans H1 donc dans
C0 pour ∥⋅ ∥∞ est égale à ψ par unicité de la minimisante de F . Par relative compacité de la suite
(fn ) pour ∥⋅ ∥∞ cela montre en fait qu’elle converge vers ψ uniformément.
2) Ceci ouvre la voie à des méthodes d’analyse numérique pour approximer ψ en prenant des suites
d’espaces En denses dans H1 comme des espaces de fonctions continues et affines par morceaux
sur [0, 1].
[Questions-Reponses]

