[Questions-Reponses]
R827. Posé dans 124 3.
Pour tous entiers p et q tels que 0 < p < q, on pose
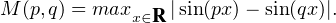
Trouver la borne inférieure de M(p,q). (Daniel Saada)
Réponse d’ric Pité
On va montrer :
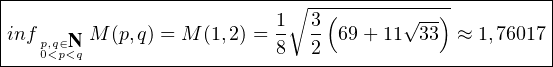
- 1.
- On calcule de façon explicite M(1,2).
- 2.
- Lorsque (p,q)≠(1,2), et q ≥ 3p on exhibe un réel yp,q tel que |sin(pyp,q) - sin(qyp,q )| > M(1,2).
- 3.
- De façon générale, lorsque (p,q)≠(1,2), on montre qu’il existe un réel yp,q (sans le trouver explicitement) tel que |sin(pyp,q) - sin(qyp,q)| > M(1,2),
On aurait pu raccourcir et passer directement à l’étape 3, mais il est instructif de voir les différentes approches. Pour paraphraser Jean Dieudonné, on pourrait résumer en trois mots : majorer, minorer, approcher.
De plus, cela nous permet d’établir des résultats asymptotiques pour M(p,q).
Quelques remarques et notations
- Pour tous entiers p et q tels que 0 < p < q, on a M(p,q) ≤ 2.
- Si p, q sont impairs et différents modulo 4, on a M(p,q) = 2. En effet, il suffit de prendre x = π⁄2.
- Pour tout tout entier k > 0, on a M(kp,kq) = M(p,q), on peut donc se borner au cas où p et q sont premiers entre eux.
- On pose fp,q(x) := sin(px) - sin(qx) = 2sin
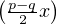 cos
cos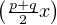 .
.
- Pour tout x réel, on note ⌈x⌉ la partie entière par excès définie par : ⌈x⌉- 1 < x ≤
⌈x⌉.
On note {x} la partie fractionnaire de x, définie par : {x} = x -⌊x⌋, où ⌊x⌋ est la partie entière de x.
Soit x tel que M(1,2) = |sin(x) - sin(2x)|, alors f1,2ʹ(x) = 0. Donc x est solution de l’équation :
4 cos 2 x - cos x - 2 = 0,
dont les solutions sur [0,π] sont x1 = arccos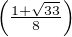 et x2 = arccos
et x2 = arccos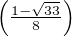 .
.
On a : 4f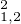 (x) =
(x) = 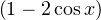 2(4sin2x). Pour x
2(4sin2x). Pour x 
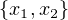 , on obtient après réduction, compte
tenu de 4 cos 2 x = cosx + 2 et 4sin2x = 2 - cosx,
, on obtient après réduction, compte
tenu de 4 cos 2 x = cosx + 2 et 4sin2x = 2 - cosx,
4f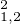 (x) =
(x) = 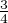
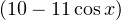 .
.
Sachant que cos est strictement décroissante sur ![[0,π]](/numeros/RMS130-3/RMS130-32715x.png) ,
,
M(1, 2) = 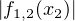 = f1,2(x2) =
= f1,2(x2) = 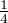
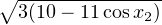 =
= 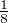
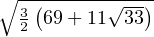 .
.
Minoration des M(1, q) pour q > 2
Lorsque q = 3 on a M(1,q) = 2.
Si q = 4 on peut utiliser la formule cos(4x) = 8cos4x - 8cos2x + 1, puis résoudre
par radicaux l’équation r4 - r2 -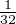 r +
r + 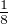 = 0. Elle possède quatre solutions réelles
distinctes. L’une d’entre elles ( ≈ 0.3616746) réalise le maximum de |f1,4|. L’expression
par radicaux prend plusieurs lignes et on ne l’écrit pas ici. Un calcul approché fournit
M(1, 4) ≈ 1, 92818.
= 0. Elle possède quatre solutions réelles
distinctes. L’une d’entre elles ( ≈ 0.3616746) réalise le maximum de |f1,4|. L’expression
par radicaux prend plusieurs lignes et on ne l’écrit pas ici. Un calcul approché fournit
M(1, 4) ≈ 1, 92818.
Lorsque q > 4, on ne peut plus utiliser la méthode précédente pour calculer explicitement
M(1, q) car on doit exprimer par radicaux les racines de polynômes de degré q, ce qui
peut être impossible lorsque q > 4. Procédons donc à présent sans le calcul explicite de
M(1, q).
Soit q > 2 un entier. Notons
xq = 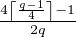 π.
π.
On a donc 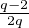 ≤
≤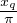 <
< 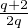 . Or, pour tout entier q > 4 on a
. Or, pour tout entier q > 4 on a
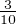 ≤
≤ 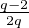 <
< 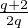 ≤
≤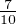 ⋅
⋅
Ainsi 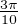 ≤ xq ≤
≤ xq ≤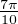 . On vérifie que cette inégalité s’étend pour q = 3 et q = 4, ce qui sera utile
par la suite. De plus, par construction,
. On vérifie que cette inégalité s’étend pour q = 3 et q = 4, ce qui sera utile
par la suite. De plus, par construction,
sin(qxq ) = -1 et sin(3π⁄10) = sin(7π⁄10) = 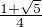 ≈ 0.80902.
≈ 0.80902.
D’où
f1,q (xq ) = 1 + sinxq ≥ 1 + sin(3π⁄10) > M(1,2).
Donc M(1, q) > M(1,2), pour tout entier q > 2.
Remarque. On voit que limq→+∞xq = 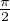 , donc limq→+∞M(1,q) = 2.
, donc limq→+∞M(1,q) = 2.
Minoration des M(p, q) pour q > p > 1
Soient q > p > 1 des entiers. Si q = 2p, on a M(p,q) = M(1,2). On aimerait procéder de façon similaire en posant
yp,q = 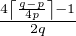 π.
π.
On a de nouveau, par construction, sin(qyp,q) = -1. De plus 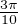 ≤ pyp,q ≤
≤ pyp,q ≤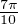 , si q ≥ 3p.
D’où
, si q ≥ 3p.
D’où
fp,q (yp,q ) = 1 + sin(pyp,q) > M(1,2), dans ces cas.
L’encadrement obtenu pour pyp,q vaut encore si q ≥ 2,143, mais cela ne suffit pas pour
conclure.
Remarque. Si p est fixé, on a limq→+∞pyp,q = 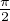 , donc limq→+∞M(p,q) = 2.
, donc limq→+∞M(p,q) = 2.
Notons g la fonction ≪ modulo 2π ≫, définie sur R par g(x) = 2π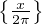 . Comme on l’a remarqué
en introduction, on peut supposer sans perte de généralité que p et q sont premiers entre eux. Pour
tout entier k naturel, on note zk = g
. Comme on l’a remarqué
en introduction, on peut supposer sans perte de généralité que p et q sont premiers entre eux. Pour
tout entier k naturel, on note zk = g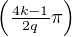 . Il suffit de montrer l’existence d’un k tel que
|fp,q (zk )| > M(1,2).
. Il suffit de montrer l’existence d’un k tel que
|fp,q (zk )| > M(1,2).
Or, on a de nouveau construit zk tel que sin(qzk) = -1. La suite 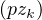 k
k N est périodique de
période exactement q. De plus, les points
N est périodique de
période exactement q. De plus, les points  exp(ipzk)
exp(ipzk)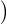 1≤k≤q se répartissent de façon équidistante
sur le cercle unité.
1≤k≤q se répartissent de façon équidistante
sur le cercle unité.
Donc, lorsque q ≥ 5, d’après le principe des tiroirs, au moins un de ces points est sur l’arc du cercle unité
{exp (iθ) | 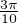 ≤ θ ≤
≤ θ ≤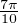 },
},
d’où l’on tire comme ci-dessus que fp,q(zk) = 1 + sin(pzk) > M(1,2).
Il ne reste plus que deux cas particuliers à traiter.
- Si (p, q) = (3,4) :
On prend z2 =
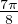 , ainsi f3,4(z2) = sin
, ainsi f3,4(z2) = sin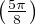 + 1 ≈ 1,92388 > M(1,2).
+ 1 ≈ 1,92388 > M(1,2).
- Si (p, q) = (2,3) :
On prend z2 =
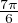 , ainsi f3,4(z2) = sin
, ainsi f3,4(z2) = sin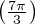 + 1 ≈ 1,86603 > M(1,2).
+ 1 ≈ 1,86603 > M(1,2).
On a ainsi prouvé le résultat annoncé.
[Questions-Reponses]

