[Questions-Reponses]
R715. Posé dans RMS 121 3.
Dans l’exercice d’oral corrigé 6 (RMS 113 4), on étudie les morphismes de GLn(K) dans un groupe abélien fini.
On propose des variantes :
a) Quels sont les morphismes de groupes de GLn(C) dans un groupe fini ? dans le groupe multiplicatif d’une extension finie de Q ? dans GLn(Q) ?
b) Quels sont les morphismes de groupes de Q dans GLn(C) ? dans GLn(Q) ? (Omar Sonebi)
Réponse de Philippe Bonnet
On dira qu’un morphisme de groupes φ : G-→Gʹ est trivial si Im(φ) = {eʹ}, où eʹ est l’élément neutre de Gʹ. Dans le premier paragraphe, on montre :
Théorème 1.Tout morphisme de GLn(C) dans un groupe de la forme G× Zr, où G est un
groupe fini et r  N, est trivial. En particulier, tout morphisme de GLn(C) dans un groupe
fini est trivial. De plus, tout morphisme de GLn(C) dans le groupe des inversibles d’une
extension finie de Q est trivial.
N, est trivial. En particulier, tout morphisme de GLn(C) dans un groupe
fini est trivial. De plus, tout morphisme de GLn(C) dans le groupe des inversibles d’une
extension finie de Q est trivial.
Dans le deuxième paragraphe, on établit les deux résultats suivants :
Théorème 2.Les morphismes de GLn(C) dans GLn(Q) sont exactement les applications φ : GL n (C )-→ GLn(Q) de la forme :
![( r [ ( ) ] )
φ:A↦- → exp ∑ αi(ln |detA |)+ βi -1-arg (detA ) Ni ,
i=1 2π](/numeros/RMS130-3/RMS130-32634x.png)
 n(Q) qui commutent deux à deux et où
α1 , … , αr , β1 , … , βr sont des formes linéaires sur le Q-espace vectoriel R, telles que β1,…,βr
soient nulles sur le Q-sous-espace vectoriel Q de R.
n(Q) qui commutent deux à deux et où
α1 , … , αr , β1 , … , βr sont des formes linéaires sur le Q-espace vectoriel R, telles que β1,…,βr
soient nulles sur le Q-sous-espace vectoriel Q de R.
Théorème 3.Les morphismes de (Q,+) dans GLn(Q) sont exactement les applications
φ : Q -→ GL n (Q), z ezN, où N est une matrice nilpotente de
ezN, où N est une matrice nilpotente de  n(Q).
n(Q).
Enfin, on va terminer avec la classification des morphismes de Q dans GLn(C). Pour ce faire, on aura besoin de décrire les morphismes de (Q,+) dans (C*,×).
En d’autres termes, une suite est admissible si le terme d’ordre n de la suite est une racine n-ième du précédent. On va se servir de ces suites pour construire tous les morphismes de (Q,+) dans (C * , ×). Plus précisément, on montre dans le deuxième paragraphe :
Proposition 1.Soit (xn)n≥1 une suite admissible de (C*)N. Alors, pour tout z  Q, la suite
((xk )⌊k!z⌋ )k≥1 est stationnaire. De plus, l’application φ(xn) : Q-→C* définie par :
Q, la suite
((xk )⌊k!z⌋ )k≥1 est stationnaire. De plus, l’application φ(xn) : Q-→C* définie par :
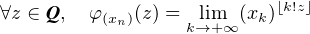
Partant de là, on démontre dans le deuxième paragraphe le résultat suivant :
Théorème 4.Les morphismes de (Q,+) dans GLn(C) sont exactement les applications de la forme :
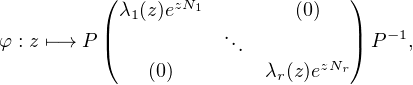
 + nr = n, où N1,…,Nr sont des matrices nilpotentes fixées de
+ nr = n, où N1,…,Nr sont des matrices nilpotentes fixées de
 n1 (C ), … ,
n1 (C ), … ,  nr (C) et où P
nr (C) et où P  GLn(C).
GLn(C).
Démonstration du premier théorème
Pour cette démonstration, on aura besoin de quelques connaissances d’Algèbre Commutative, que
l’on pourra trouver soit dans le cours d’Algèbre de Perrin, soit dans l’Algèbre Commutative de
Malliavin. Rappelons qu’un groupe G (noté multiplicativement) est divisible si, pour tout m  N* et
pour tout x
N* et
pour tout x  G, l’équation ym = x admet toujours au moins une solution dans G. En particulier,
les groupes (C * , ×) et (Q,+) sont divisibles, alors que (Z,+) ne l’est pas. Commençons par un
lemme :
G, l’équation ym = x admet toujours au moins une solution dans G. En particulier,
les groupes (C * , ×) et (Q,+) sont divisibles, alors que (Z,+) ne l’est pas. Commençons par un
lemme :
Lemme 1.Soit φ un morphisme de GLn(C) dans un groupe Gʹ au plus dénombrable. Alors on a SL n (C ) ⊂ Ker(φ). En particulier, si det : GLn(C)-→C* est le morphisme donné par le déterminant, il existe un morphisme ψ : C*-→Gʹ tel que φ = ψ • det.
Démonstration.Soit φ un morphisme de GLn(C) dans un groupe Gʹ au plus dénombrable.
Pour tout t  R , on pose :
R , on pose :
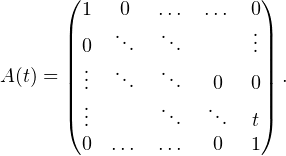
 R2, et donc A
définit un morphisme de (R,+) dans GLn(C). Par composition, l’application φ • A est un
morphisme de (R ,+) dans Gʹ. Comme Gʹ est au plus dénombrable et que R ne l’est pas, cette
application n’est pas injective, et donc Ker(φ • A) ⁄= {0}. Dès lors, il existe un réel t ⁄= 0
tel que φ • A(t) = eʹ, et donc le noyau de φ contient la transvection A(t) (qui est distincte
de l’identité car t ⁄= 0). Comme toutes les transvections de GLn(C) sont semblables entre
elles et que Ker (φ) est un sous-groupe distingué de GLn(C), Ker(φ) contient toutes
les transvections de GLn(C). Mais comme le sous-groupe SLn(C) est engendré par les
transvections, il s’ensuit que SLn(C) ⊂ Ker(φ). Dès lors, le morphisme φ induit par
passage au quotient un morphisme :
R2, et donc A
définit un morphisme de (R,+) dans GLn(C). Par composition, l’application φ • A est un
morphisme de (R ,+) dans Gʹ. Comme Gʹ est au plus dénombrable et que R ne l’est pas, cette
application n’est pas injective, et donc Ker(φ • A) ⁄= {0}. Dès lors, il existe un réel t ⁄= 0
tel que φ • A(t) = eʹ, et donc le noyau de φ contient la transvection A(t) (qui est distincte
de l’identité car t ⁄= 0). Comme toutes les transvections de GLn(C) sont semblables entre
elles et que Ker (φ) est un sous-groupe distingué de GLn(C), Ker(φ) contient toutes
les transvections de GLn(C). Mais comme le sous-groupe SLn(C) est engendré par les
transvections, il s’ensuit que SLn(C) ⊂ Ker(φ). Dès lors, le morphisme φ induit par
passage au quotient un morphisme :
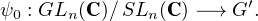
 det(A) est un isomorphisme,
on en déduit que φ = ψ • det, où ψ est le morphisme donné par ψ = ψ0 • φ
det(A) est un isomorphisme,
on en déduit que φ = ψ • det, où ψ est le morphisme donné par ψ = ψ0 • φ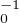 . __
. __
On commence par en montrer la première assertion. Soit φ un morphisme de GLn(C) dans un
groupe de la forme Gʹ = G× Zr, où G est un groupe fini et r  N. D’après le lemme , il existe un
morphisme ψ : C *-→Gʹ tel que φ = ψ • det. Dès lors, pour montrer que φ est trivial, il suffit de
montrer que tout morphisme ψ de C* dans le groupe Gʹ est trivial. Pour ce faire, considérons un
élément x de Im (ψ), de la forme x = (g,n1,…,nr)
N. D’après le lemme , il existe un
morphisme ψ : C *-→Gʹ tel que φ = ψ • det. Dès lors, pour montrer que φ est trivial, il suffit de
montrer que tout morphisme ψ de C* dans le groupe Gʹ est trivial. Pour ce faire, considérons un
élément x de Im (ψ), de la forme x = (g,n1,…,nr)  G× Zr. Alors il existe un élément y de C*
tel que x = ψ(y). Comme (C*,×) est divisible, il existe pour tout m
G× Zr. Alors il existe un élément y de C*
tel que x = ψ(y). Comme (C*,×) est divisible, il existe pour tout m  N* un élément ym de C* tel
que y
N* un élément ym de C* tel
que y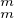 = y. Si l’on pose ψ(ym) = (hm,αm,1,…,αm,r)
= y. Si l’on pose ψ(ym) = (hm,αm,1,…,αm,r)  G × Zr, alors on a pour tout
m
G × Zr, alors on a pour tout
m  N * :
N * :
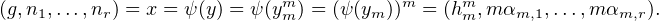
 [[1,r]]. Comme ceci est vrai pour
tout m
[[1,r]]. Comme ceci est vrai pour
tout m  N * , il s’ensuit que n1 =
N * , il s’ensuit que n1 =  = nr = 0. De plus, si m = card(G) et si e est l’élément
neutre de G, alors on sait d’après le théorème de Lagrange que h
= nr = 0. De plus, si m = card(G) et si e est l’élément
neutre de G, alors on sait d’après le théorème de Lagrange que h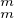 = e car hm
= e car hm  G, et
donc :
G, et
donc :
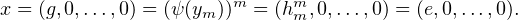
 Im (ψ), le morphisme ψ est trivial, d’où la première assertion.
Im (ψ), le morphisme ψ est trivial, d’où la première assertion.Montrons à présent la deuxième assertion du théorème . Soit L⁄Q une extension finie et
soit φ un morphisme de GLn(C) dans le groupe L* des inversibles de L⁄Q. Comme
l’extension L⁄Q est finie, L est un Q-espace vectoriel de dimension finie. En particulier,
comme Q est dénombrable, l’ensemble L est dénombrable, et donc L* l’est aussi. D’après
le lemme , il existe un morphisme ψ : C*-→L* tel que φ = ψ • det. Dès lors, pour
montrer que φ est trivial, il suffit de montrer que tout morphisme ψ de C* dans L* l’est.
Pour ce faire, fixons un morphisme ψ de C* dans L* et un élément x de Im(ψ). Soit A l’anneau
des entiers sur L, c’est-à-dire l’ensemble des éléments xʹ de L qui vérifient une équation de la
forme (xʹ)n + an-1(xʹ)n-1 +  + a0 = 0, où n
+ a0 = 0, où n  N* et an-1,…,a0
N* et an-1,…,a0  Z. Alors on sait par des
résultats classiques d’Algèbre Commutative que A est un anneau de Dedekind. En particulier,
l’anneau localisé AP est un anneau de valuation discrète pour tout idéal maximal P de A. Pour tout
idéal maximal P de A, notons vp la valuation associée sur L. Comme x appartient à Im(ψ), il
existe un élément y de C* tel que x = ψ(y). Comme (C*,×) est divisible, il existe pour tout
m
Z. Alors on sait par des
résultats classiques d’Algèbre Commutative que A est un anneau de Dedekind. En particulier,
l’anneau localisé AP est un anneau de valuation discrète pour tout idéal maximal P de A. Pour tout
idéal maximal P de A, notons vp la valuation associée sur L. Comme x appartient à Im(ψ), il
existe un élément y de C* tel que x = ψ(y). Comme (C*,×) est divisible, il existe pour tout
m  N * un élément ym de C* tel que y
N * un élément ym de C* tel que y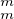 = y. En termes de valuations, ceci nous donne
que :
= y. En termes de valuations, ceci nous donne
que :
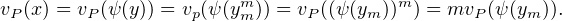
 N*, et donc vP(x) = 0. Dès lors, les
éléments x et
N*, et donc vP(x) = 0. Dès lors, les
éléments x et  appartiennent à AP car AP est de valuation discrète. Comme A est égal à
l’intersection des localisés AP lorsque P parcourt l’ensemble des idéaux maximaux de A, il
s’ensuit que x et
appartiennent à AP car AP est de valuation discrète. Comme A est égal à
l’intersection des localisés AP lorsque P parcourt l’ensemble des idéaux maximaux de A, il
s’ensuit que x et  appartiennent tous deux à A. En particulier, x est inversible dans l’anneau A.
Comme ceci est vrai pour tout x
appartiennent tous deux à A. En particulier, x est inversible dans l’anneau A.
Comme ceci est vrai pour tout x  Im(ψ), il s’ensuit que Im(ψ) est contenue dans le groupe
U(A) des inversibles de l’anneau A, que l’on appelle communément le groupe des unités
de A. Dès lors, on peut considérer que ψ est un morphisme de C* dans U(A). Or on
sait d’après le théorème des unités de Dirichlet que U(A) est isomorphe à un groupe
de la forme G × Zr, où G est fini et r
Im(ψ), il s’ensuit que Im(ψ) est contenue dans le groupe
U(A) des inversibles de l’anneau A, que l’on appelle communément le groupe des unités
de A. Dès lors, on peut considérer que ψ est un morphisme de C* dans U(A). Or on
sait d’après le théorème des unités de Dirichlet que U(A) est isomorphe à un groupe
de la forme G × Zr, où G est fini et r  N. Dès lors, il s’ensuit d’après la première
assertion du théorème que le morphisme ψ est trivial, et donc φ l’est aussi, d’où le résultat.
□
N. Dès lors, il s’ensuit d’après la première
assertion du théorème que le morphisme ψ est trivial, et donc φ l’est aussi, d’où le résultat.
□
Démonstration des autres théorèmes
Passons maintenant aux morphismes de GLn(C) dans GLn(Q), de (Q,+) dans GLn(Q) et de (Q , +) dans GL n(C). Pour ce faire, on commence par établir quelques lemmes :
Lemme 2.Les morphismes de (C*,×) dans (Q,+) sont exactement les applications φ de C*dans Q de la forme :
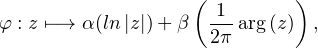
Démonstration.Commençons par montrer que toute application φ de la forme donnée plus
haut est un morphisme bien défini de C* dans Q. Pour ce faire, fixons des formes linéaires
α, β sur le Q -espace vectoriel R, telles que β soit nulle sur le Q-sous-espace vectoriel Q de
R. Comme le module est un morphisme de (C*,×) dans (R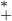 ,×), que la fonction ln est un
morphisme de (R
,×), que la fonction ln est un
morphisme de (R 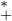 ,×) dans (R,+) et que α est un morphisme de (R,+) dans (Q,+) (vu
que c’est une forme Q-linéaire), on obtient par composition que l’application z
,×) dans (R,+) et que α est un morphisme de (R,+) dans (Q,+) (vu
que c’est une forme Q-linéaire), on obtient par composition que l’application z α(ln|z|)
est un morphisme de (C*,×) dans (Q,+). De plus, d’après les propriétés de l’argument
d’un nombre complexe non nul, on voit que l’application z
α(ln|z|)
est un morphisme de (C*,×) dans (Q,+). De plus, d’après les propriétés de l’argument
d’un nombre complexe non nul, on voit que l’application z
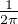 arg(z) est un morphisme
bien défini de (C *,×) dans (R⁄Z,+). Mais comme β est une forme linéaire sur le Q-espace
vectoriel R qui s’annule sur Q, β est un morphisme de (R,+) dans (Q,+) qui s’annule sur
Z, et donc on trouve par composition que l’application z
arg(z) est un morphisme
bien défini de (C *,×) dans (R⁄Z,+). Mais comme β est une forme linéaire sur le Q-espace
vectoriel R qui s’annule sur Q, β est un morphisme de (R,+) dans (Q,+) qui s’annule sur
Z, et donc on trouve par composition que l’application z β(
β(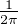 arg(z)) est un morphisme
bien défini de (C *,×) dans (Q,+). Par addition, il s’ensuit que φ est bien un morphisme
bien défini de (C *,×) dans (Q,+).
arg(z)) est un morphisme
bien défini de (C *,×) dans (Q,+). Par addition, il s’ensuit que φ est bien un morphisme
bien défini de (C *,×) dans (Q,+).
Réciproquement, montrons que tout morphisme φ de (C*,×) dans (Q,+) doit être de cette
forme. Pour tout y  R, on note
R, on note 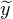 sa classe dans R⁄Z. Avec les propriétés du module, de
l’argument et du logarithme, on vérifie facilement que l’application :
sa classe dans R⁄Z. Avec les propriétés du module, de
l’argument et du logarithme, on vérifie facilement que l’application :
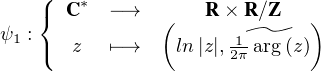
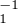 , alors on
constate que φ = φ1 •ψ1 et que φ1 est un morphisme de (R × R⁄Z,+) dans (Q,+). Si l’on
pose α(x) = φ1 (x,0) et β(y) = φ1(0,
, alors on
constate que φ = φ1 •ψ1 et que φ1 est un morphisme de (R × R⁄Z,+) dans (Q,+). Si l’on
pose α(x) = φ1 (x,0) et β(y) = φ1(0,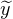 ) pour tout (x,y)
) pour tout (x,y)  R2, alors on vérifie facilement
que α et β sont des morphismes bien définis de (R,+) dans (Q,+). De plus, comme φ1 est
un morphisme de (R × R⁄Z,+) dans (Q,+), on a pour tout (x,
R2, alors on vérifie facilement
que α et β sont des morphismes bien définis de (R,+) dans (Q,+). De plus, comme φ1 est
un morphisme de (R × R⁄Z,+) dans (Q,+), on a pour tout (x,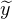 )
)  R × R⁄Z (si y désigne
un représentant de
R × R⁄Z (si y désigne
un représentant de 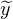 ) :
) :
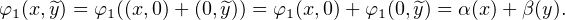
 C* :
C* :
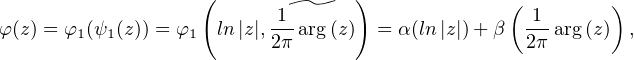
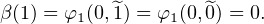
Lemme 3.Soient l1,…lr des morphismes de (C*,×) dans (Q,+) et soient N1,…,Nr des
matrices nilpotentes de  n(Q) qui commutent deux à deux. Alors l’application :
n(Q) qui commutent deux à deux. Alors l’application :
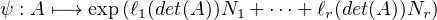
Démonstration.Soient l1,…lr des morphismes de (C*,×) dans (Q,+), soient N1,…,Nr des
matrices nilpotentes de  n(Q) qui commutent deux à deux et considérons l’application ψ1
de C * dans
n(Q) qui commutent deux à deux et considérons l’application ψ1
de C * dans  n (C) donnée par :
n (C) donnée par :
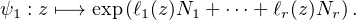
 + lr(z)Nr est une
matrice nilpotente de
+ lr(z)Nr est une
matrice nilpotente de  n(Q) pour tout z
n(Q) pour tout z  C*. En particulier, son exponentielle ne compte
qu’un nombre fini de termes, et donc ψ1(z) appartient bien à GLn(Q) pour tout z
C*. En particulier, son exponentielle ne compte
qu’un nombre fini de termes, et donc ψ1(z) appartient bien à GLn(Q) pour tout z  C*. De
plus, comme N1 ,…,Nr commutent deux à deux, les matrices l1(z)N1 +
C*. De
plus, comme N1 ,…,Nr commutent deux à deux, les matrices l1(z)N1 +  + lr(z)Nr et
l1 (zʹ)N1 +
+ lr(z)Nr et
l1 (zʹ)N1 + +lr(zʹ)Nr commutent pour tous z,zʹ
+lr(zʹ)Nr commutent pour tous z,zʹ C*. Comme les applications l1,…,lr
sont des morphismes de C* dans Q, il s’ensuit que, pour tous z,zʹ
C*. Comme les applications l1,…,lr
sont des morphismes de C* dans Q, il s’ensuit que, pour tous z,zʹ C* :
C* :
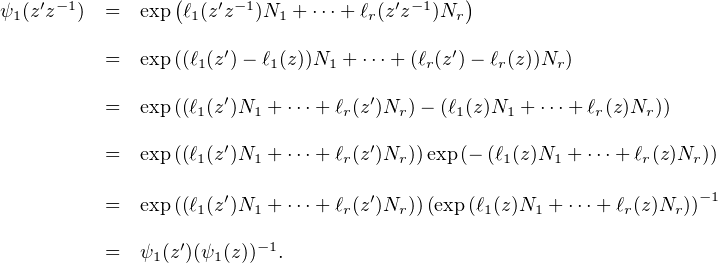
Lemme 4.Soit ψ un morphisme de (C*,×) dans GLn(Q). Alors ψ(z) est une matrice
unipotente de GLn(Q) pour tout z  C*, c’est-à-dire : Sp(ψ(z)) = {1}.
C*, c’est-à-dire : Sp(ψ(z)) = {1}.
Démonstration.Fixons un morphisme ψ de C* dans GLn(Q) ; notons Q la clôture
algébrique de Q et posons G = Im(ψ). Comme (C*,×) est commutatif, le groupe G
est un sous-groupe commutatif de GLn(Q), et donc aussi de GLn(Q). Comme Q est
algébriquement clos, tous les éléments de G sont cotrigonalisables dans une même base de
Qn. Dès lors, il existe une matrice P = (pi,j)  GLn(Q) telle que toutes les matrices de la
forme P-1 AP, où A appartient à G, sont triangulaires supérieures. Posons alors :
GLn(Q) telle que toutes les matrices de la
forme P-1 AP, où A appartient à G, sont triangulaires supérieures. Posons alors :
![L = Q[p1,1,...,p1,n,...,pn,1,...,pn,n].](/numeros/RMS130-3/RMS130-32676x.png)
 P-1ψ(z)P
est à valeurs dans l’ensemble Tn(L) des matrices triangulaires supérieures de taille n et à
coefficients dans L. noter que ψ0 est bien un morphisme comme composée du morphisme ψ
et d’un automorphisme intérieur de GLn(L). De plus, il est de la forme :
P-1ψ(z)P
est à valeurs dans l’ensemble Tn(L) des matrices triangulaires supérieures de taille n et à
coefficients dans L. noter que ψ0 est bien un morphisme comme composée du morphisme ψ
et d’un automorphisme intérieur de GLn(L). De plus, il est de la forme :

 [[1, n]] et pour tous z,zʹ
[[1, n]] et pour tous z,zʹ C*. En particulier, chaque λi est un morphisme de
C*dans L* . Comme L⁄Q est une extension finie, il s’ensuit d’après le théorème que tous les
morphismes λi sont triviaux. En particulier, la matrice ψ0(z) n’a que des 1 sur sa diagonale,
et donc elle est unipotente pour tout z
C*. En particulier, chaque λi est un morphisme de
C*dans L* . Comme L⁄Q est une extension finie, il s’ensuit d’après le théorème que tous les
morphismes λi sont triviaux. En particulier, la matrice ψ0(z) n’a que des 1 sur sa diagonale,
et donc elle est unipotente pour tout z  C*. Par similitude, la matrice ψ(z) est unipotente
pour tout z
C*. Par similitude, la matrice ψ(z) est unipotente
pour tout z  C * . __
C * . __
D’après les lemmes et , on voit que, si N1,…,Nr sont des matrices nilpotentes de  n(Q) qui
commutent deux à deux et si α1,…,αr,β1,…,βr sont des formes linéaires sur le Q-espace
vectoriel R , telles que β1,…,βr sont nulles sur le Q-sous-espace vectoriel Q de R, alors
l’application :
n(Q) qui
commutent deux à deux et si α1,…,αr,β1,…,βr sont des formes linéaires sur le Q-espace
vectoriel R , telles que β1,…,βr sont nulles sur le Q-sous-espace vectoriel Q de R, alors
l’application :
![( r [ ( )] )
φ:A↦-→ exp ∑ αi(ln |det(A)|)+ βi -1-arg(det(A )) Ni
i=1 2π](/numeros/RMS130-3/RMS130-32679x.png)
Reste donc à montrer que tout morphisme φ de GLn(C) dans GLn(Q) doit être de cette forme.
Pour ce faire, fixons un morphisme φ de GLn(C) dans GLn(Q). Comme GLn(Q) est un
sous-ensemble de  n(Q), qui est un espace vectoriel de dimension finie sur Q, GLn(Q) est au
plus dénombrable. D’après le lemme , il existe un morphisme ψ : C*-→GLn(Q) tel que
φ = ψ • det . Dès lors, pour montrer que φ est de la forme annoncée dans le théorème , il suffit au
vu du lemme de vérifier que tout morphisme ψ de (C*,×) dans GLn(Q) est de la
forme :
n(Q), qui est un espace vectoriel de dimension finie sur Q, GLn(Q) est au
plus dénombrable. D’après le lemme , il existe un morphisme ψ : C*-→GLn(Q) tel que
φ = ψ • det . Dès lors, pour montrer que φ est de la forme annoncée dans le théorème , il suffit au
vu du lemme de vérifier que tout morphisme ψ de (C*,×) dans GLn(Q) est de la
forme :
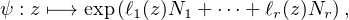
 n(Q) qui commutent deux à deux.
n(Q) qui commutent deux à deux. Pour ce faire, considérons un morphisme ψ de (C*,×) dans GLn(Q), et posons Mz = ψ(z) -In
pour tout z  C * . Comme ψ(z) est unipotente pour tout z
C * . Comme ψ(z) est unipotente pour tout z  C* d’après le lemme , la matrice Mz
appartient à
C* d’après le lemme , la matrice Mz
appartient à  n (Q) et est nilpotente pour tout z
n (Q) et est nilpotente pour tout z  C*. Dès lors, comme l’exponentielle est un
homéomorphisme de l’ensemble des matrices nilpotentes de
C*. Dès lors, comme l’exponentielle est un
homéomorphisme de l’ensemble des matrices nilpotentes de  n(C) dans l’ensemble des matrices
unipotentes de GLn(C), il existe pour tout z
n(C) dans l’ensemble des matrices
unipotentes de GLn(C), il existe pour tout z  C* une unique matrice nilpotente de
C* une unique matrice nilpotente de  n(C), notée
N(z), telle que eN(z) = ψ(z). noter que, comme la bijection réciproque est donnée par le
logarithme (lequel est bien défini car les matrices en question sont nilpotentes d’indice ≤ n), on a
la relation :
n(C), notée
N(z), telle que eN(z) = ψ(z). noter que, comme la bijection réciproque est donnée par le
logarithme (lequel est bien défini car les matrices en question sont nilpotentes d’indice ≤ n), on a
la relation :
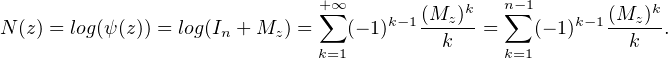
 n(Q) et que la somme de droite est finie, on
voit que toutes les matrices N(z) appartiennent à
n(Q) et que la somme de droite est finie, on
voit que toutes les matrices N(z) appartiennent à  n(Q). Qui plus est, comme (C*,×) est
commutatif, toutes les matrices de la forme ψ(z) commutent entre elles. Comme Mz = ψ(z) -In
pour tout z
n(Q). Qui plus est, comme (C*,×) est
commutatif, toutes les matrices de la forme ψ(z) commutent entre elles. Comme Mz = ψ(z) -In
pour tout z  C * , toutes les matrices Mz commutent entre elles. En particulier, comme N(z) est un
polynôme en Mz pour tout z
C * , toutes les matrices Mz commutent entre elles. En particulier, comme N(z) est un
polynôme en Mz pour tout z  C*, toutes les matrices N(z) commutent entre elles. Si E désigne le
Q-espace vectoriel engendré par toutes les matrices N(z) lorsque z parcourt C*, alors on constate
que E est un sous-espace vectoriel de
C*, toutes les matrices N(z) commutent entre elles. Si E désigne le
Q-espace vectoriel engendré par toutes les matrices N(z) lorsque z parcourt C*, alors on constate
que E est un sous-espace vectoriel de  n(Q) formé de matrices nilpotentes qui commutent deux à
deux. De plus, N est une application de C* dans E par construction. Partant du fait que ψ est
un morphisme et que toutes les matrices N(z) commutent entre elles, on a pour tous
z, zʹ
n(Q) formé de matrices nilpotentes qui commutent deux à
deux. De plus, N est une application de C* dans E par construction. Partant du fait que ψ est
un morphisme et que toutes les matrices N(z) commutent entre elles, on a pour tous
z, zʹ  C * :
C * :
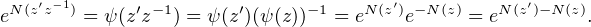
 n(C) dans l’ensemble des matrices unipotentes de GLn(C), il s’ensuit que
N(zʹz-1 ) = N(zʹ) - N(z) pour tous z,zʹ
n(C) dans l’ensemble des matrices unipotentes de GLn(C), il s’ensuit que
N(zʹz-1 ) = N(zʹ) - N(z) pour tous z,zʹ C, et donc N est un morphisme de (C*,×) dans E.
Fixons une base (N1,…,Nr) du Q-espace vectoriel E. Alors, pour tout z
C, et donc N est un morphisme de (C*,×) dans E.
Fixons une base (N1,…,Nr) du Q-espace vectoriel E. Alors, pour tout z  C*, il existe des uniques
nombres rationnels l1(z),…,lr(z) tels que :
C*, il existe des uniques
nombres rationnels l1(z),…,lr(z) tels que :
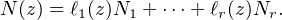
 C*, on
en déduit que le morphisme ψ est bien de la forme :
C*, on
en déduit que le morphisme ψ est bien de la forme :
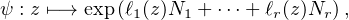
Commençons par montrer que tout morphisme φ de Q dans GLn(Q) doit être de la forme
annoncée dans le théorème . Comme (Q,+) est divisible, on obtient en reproduisant mot pour mot
la démonstration du théorème que tout morphisme de (Q,+) dans le groupe des inversibles d’une
extension finie L⁄Q est forcément trivial. Partant de là, on vérifie comme dans la démonstration du
théorème qu’il existe une famille de morphismes l1,…,lr de (Q,+) dans (Q,+) et une
famille de matrices nilpotentes N1,…,Nr de  n(Q) qui commutent deux à deux telles
que :
n(Q) qui commutent deux à deux telles
que :
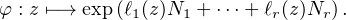
 aiz, où ai
aiz, où ai  Q. Si
l’on pose N = a1N1 +
Q. Si
l’on pose N = a1N1 +  + arNr, alors on vérifie sans peine que la matrice N est
nilpotente (car toutes les matrices Ni sont nilpotentes et commutent deux à deux), et que de
plus φ(x) = exN pour tout x
+ arNr, alors on vérifie sans peine que la matrice N est
nilpotente (car toutes les matrices Ni sont nilpotentes et commutent deux à deux), et que de
plus φ(x) = exN pour tout x  Q. Quant à la réciproque, elle découle directement des
propriétés de l’exponentielle de matrices, ce qui conclut la démonstration du théorème
.
Q. Quant à la réciproque, elle découle directement des
propriétés de l’exponentielle de matrices, ce qui conclut la démonstration du théorème
.
Démonstration de la proposition
Considérons une suite (xn)n≥1 admissible de (C*)N. Il s’agit tout d’abord de montrer que la suite
((xk )⌊k!z⌋ )k≥1 est stationnaire pour tout z  Q. Pour ce faire, fixons un nombre rationnel z, que
l’on écrit sous la forme z =
Q. Pour ce faire, fixons un nombre rationnel z, que
l’on écrit sous la forme z = 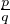 , où p
, où p  Z et q
Z et q  N*. Alors, pour tout entier k ≥ q, on voit que k!z est
un entier, et donc ⌊k!z⌋ = k!z et ⌊(k + 1)!z⌋ = (k + 1)!z = (k + 1)k!z. En particulier, on a pour
tout k ≥ q :
N*. Alors, pour tout entier k ≥ q, on voit que k!z est
un entier, et donc ⌊k!z⌋ = k!z et ⌊(k + 1)!z⌋ = (k + 1)!z = (k + 1)k!z. En particulier, on a pour
tout k ≥ q :
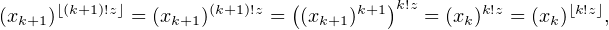
 limk→+∞(xk)⌊k!z⌋ est bien définie.
limk→+∞(xk)⌊k!z⌋ est bien définie.Montrons maintenant que cette application est un morphisme de (Q,+) dans (C*,×). Pour ce faire,
considérons deux nombres rationnels z,zʹ, que l’on écrit sous la forme z = 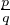 et zʹ =
et zʹ = 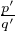 , où
p, pʹ
, où
p, pʹ  Z et q, qʹ
Z et q, qʹ  N*. Alors, pour tout entier k ≥ q + qʹ, on constate que k!z,k!zʹ,k!(z -zʹ) sont
des entiers, et donc :
N*. Alors, pour tout entier k ≥ q + qʹ, on constate que k!z,k!zʹ,k!(z -zʹ) sont
des entiers, et donc :
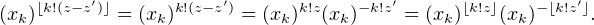
 Q :
Q :
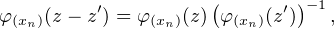
Enfin, montrons que tout morphisme de (Q,+) dans (C*,×) est de la forme φ(xn), où (xn)n≥1 est
une suite admissible de (C*)N. Pour ce faire, considérons un morphisme φ de (Q,+) dans (C*,×),
et posons pour tout n  N* :
N* :
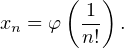
 N* :
N* :
![[ ( 1 ) ]n+1 ( n+ 1 ) ( 1)
(xn+1)n+1 = φ (n+-1)! = φ (n-+-1)!- = φ n! = xn.](/numeros/RMS130-3/RMS130-32696x.png)
 N* est admissible. Reste à montrer que φ = φ(xn). Pour ce faire, fixons
un élément z de Q, que l’on écrit sous la forme z =
N* est admissible. Reste à montrer que φ = φ(xn). Pour ce faire, fixons
un élément z de Q, que l’on écrit sous la forme z = 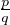 , où p
, où p  Z et q
Z et q  N*. Alors, pour tout entier
k ≥ q, on voit que k!z est un entier, et donc ⌊k!z⌋ = k!z. En particulier, comme φ est un morphisme
de groupes, on a pour tout k ≥ q :
N*. Alors, pour tout entier
k ≥ q, on voit que k!z est un entier, et donc ⌊k!z⌋ = k!z. En particulier, comme φ est un morphisme
de groupes, on a pour tout k ≥ q :
![[ ( ) ]k!z ( )
(xk)⌊k!z⌋ = (xk)k!z = φ 1- = φ k!z- = φ (z).
k! k!](/numeros/RMS130-3/RMS130-32698x.png)
 Q , on en déduit que φ(xn) = φ, d’où le résultat.
Q , on en déduit que φ(xn) = φ, d’où le résultat.
l’aide des propriétés des matrices diagonales par blocs, il est facile de vérifier que toute application
de la forme donnée dans le théorème est bien un morphisme de (Q,+) dans GLn(C).
Reste à établir la réciproque. Pour ce faire, considérons un morphisme φ de (Q,+) dans
GLn(C ). Comme (Q,+) est abélien, le groupe Im(φ) est un sous-groupe commutatif de
GLn(C ). En particulier, tous ses éléments sont cotrigonalisables. Dès lors, il est facile
de vérifier par récurrence sur n qu’il existe une matrice P  GLn(C) et des entiers
n1 , … , nr > 0 (avec n = n1 +
GLn(C) et des entiers
n1 , … , nr > 0 (avec n = n1 +  + nr) tels que, pour tout z
+ nr) tels que, pour tout z  Q, la matrice φ(z) est de la
forme :
Q, la matrice φ(z) est de la
forme :
![( )
λ1(z)[In1 + M1 (z)] (0)
φ(z)= P |( ... |) P-1,
(0) λr(z)[Inr + Mr (z)]](/numeros/RMS130-3/RMS130-32700x.png)
 n1 (C ), … ,
n1 (C ), … ,  nr (C). Comme l’exponentielle est un homéomorphisme de l’ensemble des matrices
nilpotentes de
nr (C). Comme l’exponentielle est un homéomorphisme de l’ensemble des matrices
nilpotentes de  n(C) dans l’ensemble des matrices unipotentes de GLn(C), il existe pour tout
i
n(C) dans l’ensemble des matrices unipotentes de GLn(C), il existe pour tout
i  [[1, r]] et pour tout z
[[1, r]] et pour tout z  C* une unique matrice nilpotente de
C* une unique matrice nilpotente de  ni(C), notée Niʹ(z), telle que
eNi ʹ(z) = In
i + Mi(z). Comme φ est un morphisme de groupes, on vérifie facilement par le calcul
que, pour tout i
ni(C), notée Niʹ(z), telle que
eNi ʹ(z) = In
i + Mi(z). Comme φ est un morphisme de groupes, on vérifie facilement par le calcul
que, pour tout i  [[1,r]] et pour tous z,zʹ
[[1,r]] et pour tous z,zʹ Q :
Q :
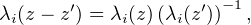
 [[1,r]], l’application
Ni ʹ est un morphisme de (Q,+) dans
[[1,r]], l’application
Ni ʹ est un morphisme de (Q,+) dans  ni(C), puis qu’il existe une matrice Ni de
ni(C), puis qu’il existe une matrice Ni de  ni(C) telle
que Ni ʹ(z) = zNi pour tout z
ni(C) telle
que Ni ʹ(z) = zNi pour tout z  Q et enfin que Ni est nilpotente. En particulier, il s’ensuit que,
pour tout z
Q et enfin que Ni est nilpotente. En particulier, il s’ensuit que,
pour tout z  Q :
Q :
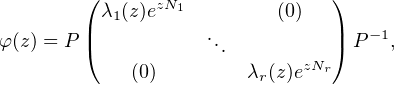
La question a été résolue par l’auteur.
[Questions-Reponses]

