[Questions-Reponses]
R648. Posé dans RMS 119 3
Soit L un corps, K un sous-corps de L et deux entiers naturels non nuls n et N. tant donné
deux N-uplets (A1,…,AN) 
 n(K)N et (B1,…,BN)
n(K)N et (B1,…,BN) 
 n(K)N, l’existence d’une matrice
inversible P
n(K)N, l’existence d’une matrice
inversible P  GLn(L) telle que ∀k
GLn(L) telle que ∀k  [[1,N]],Bk = PAkP-1 implique-t-elle celle d’une
matrice inversible Q
[[1,N]],Bk = PAkP-1 implique-t-elle celle d’une
matrice inversible Q  GLn(K) telle que ∀k
GLn(K) telle que ∀k  [[1,N]]Bk = QAkQ-1 ?
(Clément de Seguins Pazzis)
[[1,N]]Bk = QAkQ-1 ?
(Clément de Seguins Pazzis)
Réponse de l’auteur de la question
La réponse est oui. Le résultat est essentiellement une reformulation du lemme de Noether-Deuring, bien connu des spécialistes de théorie des représentations, et qui s’énonce comme suit.
Théorème 1 (Lemme de Noether-Deuring). Soit L un corps, K un sous-corps de L et n un
entier naturel non nul. Soit  une K-algèbre, et φ :
une K-algèbre, et φ :  →
→  n(K) et ψ :
n(K) et ψ :  →
→  n(K)
deux morphismes de K-algèbres. On suppose que φ et ψ sont L-conjuguées, c’est-à-dire
qu’il existe P
n(K)
deux morphismes de K-algèbres. On suppose que φ et ψ sont L-conjuguées, c’est-à-dire
qu’il existe P  GLn(L) telle que Pφ(x) = ψ(x)P pour tout x
GLn(L) telle que Pφ(x) = ψ(x)P pour tout x 
 . Alors φ et ψ sont
K-conjuguées.
. Alors φ et ψ sont
K-conjuguées.
Expliquons d’abord l’équivalence entre ces deux résultats.
Supposons acquis le lemme de Noether-Deuring et plaçons-nous sous les hypothèses de la question.
Considérons alors l’algèbre  des polynômes en n indéterminées non commutant X1,…,XN et à
coefficients dans K, et les morphismes ψ :
des polynômes en n indéterminées non commutant X1,…,XN et à
coefficients dans K, et les morphismes ψ :  →
→ n(K) et φ :
n(K) et φ :  →
→ n(K) définis par les
conditions ψ(Xk ) = Ak et φ(Xk) = Bk pour tout k
n(K) définis par les
conditions ψ(Xk ) = Ak et φ(Xk) = Bk pour tout k  [[1,N]]. Si (A1,…,AN) est simultanément
conjuguée à (B1 ,…,BN) sur L, alors φ et ψ sont L-conjuguées, donc K-conjuguées par le lemme
de Noether-Deuring, et on obtient alors que (A1,…,AN) est simultanément conjuguée à
(B1 , … , BN ) sur K.
[[1,N]]. Si (A1,…,AN) est simultanément
conjuguée à (B1 ,…,BN) sur L, alors φ et ψ sont L-conjuguées, donc K-conjuguées par le lemme
de Noether-Deuring, et on obtient alors que (A1,…,AN) est simultanément conjuguée à
(B1 , … , BN ) sur K.
Réciproquement, supposons acquis notre résultat et plaçons-nous sous les hypothèses du lemme de Noether-Deuring.
Les applications K-linéaires φ et ψ ont clairement même noyau, noté V , de codimension finie (non
nulle) dans  . On prend une base (C1,…,CN) d’un supplémentaire de ce noyau. On
applique alors le résultat de notre question aux listes (A1,…,AN) := (φ(C1),…,φ(CN)) et
(B1 , … , BN ) := (ψ(C1),…,ψ(CN)), qui sont simultanément conjuguées sur L. On obtient donc
Q
. On prend une base (C1,…,CN) d’un supplémentaire de ce noyau. On
applique alors le résultat de notre question aux listes (A1,…,AN) := (φ(C1),…,φ(CN)) et
(B1 , … , BN ) := (ψ(C1),…,ψ(CN)), qui sont simultanément conjuguées sur L. On obtient donc
Q  GL n (K ) telle que Qφ(Ci) = ψ(Ci)Q pour tout i
GL n (K ) telle que Qφ(Ci) = ψ(Ci)Q pour tout i  [[1,N]], puis les fonctions K-linéaires
x
[[1,N]], puis les fonctions K-linéaires
x 

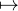 Qφ(x) et x
Qφ(x) et x 

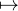 ψ(x)Q coïncident sur Kerφ et V ect(C1,…,CN) donc elles sont
égales.
ψ(x)Q coïncident sur Kerφ et V ect(C1,…,CN) donc elles sont
égales.
Il reste bien entendu à démontrer le lemme de Noether-Deuring. Toutes les démonstrations connues à ce jour séparent la démonstration en deux sous-cas, le plus délicat étant celui où K est un corps fini.
Le cas où K est de cardinal supérieur ou égal à n est commun à toutes les démonstrations connues
et reprend l’argumentation classique du cas N = 1 : on part de P  GLn(L) telle que
Pψ(x) = φ(x)P pour tout x
GLn(L) telle que
Pψ(x) = φ(x)P pour tout x 
 . On note V le sous-K-espace vectoriel de L engendré par les
coefficients de P, et (λ1,…,λd) une base de celui-ci, si bien que P =
. On note V le sous-K-espace vectoriel de L engendré par les
coefficients de P, et (λ1,…,λd) une base de celui-ci, si bien que P = 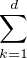 λiPi pour des matrices
P1 , … , Pd de
λiPi pour des matrices
P1 , … , Pd de  n (K). Par identification des coordonnées dans la K-base (λ1,…,λd) de V , on voit
que, pour tout x
n (K). Par identification des coordonnées dans la K-base (λ1,…,λd) de V , on voit
que, pour tout x 
 , l’identité Pψ(x) = φ(x)P se traduit par ∀i
, l’identité Pψ(x) = φ(x)P se traduit par ∀i  [[1,d]],Piψ(x) = φ(x)Pi et
donne donc Qψ(x) = φ(x)Q pour tout Q
[[1,d]],Piψ(x) = φ(x)Pi et
donne donc Qψ(x) = φ(x)Q pour tout Q  V ectK(P1,…,Pd). Il suffit pour conclure de montrer
que V ect K (P1 , …,Pd) contient une matrice inversible. Pour cela, on remarque que la
fonction
V ectK(P1,…,Pd). Il suffit pour conclure de montrer
que V ect K (P1 , …,Pd) contient une matrice inversible. Pour cela, on remarque que la
fonction
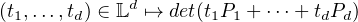
Nous allons maintenant exposer la démonstration classique, qui règle de manière directe le cas où L est une extension finie de K. En combinant ce résultat avec le précédent, il est facile de conclure : si en effet K est fini et L en est une extension infinie, on peut commencer par plonger L dans une clôture algébrique L, puis trouver une extension intermédiaire K - Kʹ-L de degré fini sur K et de cardinal supérieur ou égal à n ; comme les représentations φ et ψ sont conjuguées sur L, elles le sont en particulier sur L, donc sur Kʹ par la première étape. Il suffira donc de traiter le cas d’une extension finie pour redescendre à K.
Pour les extensions finies, la démonstration la plus classique repose sur un résultat à la fois profond
et très universel de théorie de représentation des modules, le théorème de Krull-Schmidt. Pour
éviter d’introduire une quantité importante de notions, nous nous limitons aux modules sur la
K-algèbre  qui sont de dimension finie sur K (pour la structure de K-espace vectoriel déduite de
leur structure de module).
qui sont de dimension finie sur K (pour la structure de K-espace vectoriel déduite de
leur structure de module).
Un  -module de dimension finie sur K est dit indécomposable lorsqu’il est non nul et n’est pas la
somme directe de deux sous-modules non-triviaux. Tout
-module de dimension finie sur K est dit indécomposable lorsqu’il est non nul et n’est pas la
somme directe de deux sous-modules non-triviaux. Tout  -module de dimension finie sur K se
décompose comme somme directe finie de sous-modules indécomposables (tous ceux-ci sont
évidemment de dimension finie sur K).
-module de dimension finie sur K se
décompose comme somme directe finie de sous-modules indécomposables (tous ceux-ci sont
évidemment de dimension finie sur K).
Théorème 2 (Krull-Schmidt). Soit M1,…,Mp,N1,…,Nq des  -modules indécomposables
de dimension finie sur K tels que M1 ⊕
-modules indécomposables
de dimension finie sur K tels que M1 ⊕ ⊕ Mp soit isomorphe à M1 ⊕
⊕ Mp soit isomorphe à M1 ⊕ ⊕ Mq. Alors
p = q et il existe σ
⊕ Mq. Alors
p = q et il existe σ  𝔖p tel que Mi soit isomorphe à Mσ(i) pour tout i
𝔖p tel que Mi soit isomorphe à Mσ(i) pour tout i  {1,…,p}.
{1,…,p}.
Ici, M1 ⊕  ⊕ Md désigne la somme directe extérieure des modules M1,…,Mq, que l’on définit
comme le produit cartésien M1 ×
⊕ Md désigne la somme directe extérieure des modules M1,…,Mq, que l’on définit
comme le produit cartésien M1 × × Md muni de la structure naturelle de
× Md muni de la structure naturelle de  -module
produit.
-module
produit.
Une démonstration détaillée du théorème de Krull-Schmidt est donnée en annexe à
notre réponse. Contentons-nous de quelques remarques : le lecteur au fait de la théorie
des représentations de groupes finis a reconnu, pour l’algèbre de groupes C[G] d’un
groupe fini G, l’énoncé correspondant sur l’unicité de la décomposition en représentations
irréductibles sur C (moyennant le lemme de Maschke, qui permet de voir en les représentations
irréductibles complexes de G les C[G]-modules indécomposables de dimension finie sur C). La
démonstration du théorème de Krull-Schmidt est essentiellement fondée sur le même
principe mais est rendue sensiblement plus compliquée par une différence importante :
alors qu’est nul tout morphisme entre deux représentations irréductibles complexes non
isomorphes, il peut exister des morphismes non nuls entre  -modules indécomposables
non-isomorphes !
-modules indécomposables
non-isomorphes !
Nous allons maintenant voir comment le théorème de Krull-Schmidt permet d’obtenir le lemme de
Noether-Deuring dans le cas où L est de dimension finie d sur K. Considérons le  -module M
(respectivement N) dont l’ensemble sous-jacent est Kn et la loi externe définie comme
x.X := φ(x)X (respectivement x.X := ψ(x)X) pour tout x
-module M
(respectivement N) dont l’ensemble sous-jacent est Kn et la loi externe définie comme
x.X := φ(x)X (respectivement x.X := ψ(x)X) pour tout x 
 et tout X
et tout X  Kn. On définit de
même des
Kn. On définit de
même des  -modules ML et NL en partant de Ln au lieu de Kn. l’aide d’une base de L sur K, on
démontre sans peine que ML est isomorphe, en tant que
-modules ML et NL en partant de Ln au lieu de Kn. l’aide d’une base de L sur K, on
démontre sans peine que ML est isomorphe, en tant que  -module, à la somme directe externe de d
copies de M.
-module, à la somme directe externe de d
copies de M.
Un isomorphisme de  -modules de M sur N est en particulier un isomorphisme pour les K-espaces
vectoriels sous-jacents. C’est donc une fonction de la forme θ : X
-modules de M sur N est en particulier un isomorphisme pour les K-espaces
vectoriels sous-jacents. C’est donc une fonction de la forme θ : X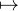 QX où Q
QX où Q  GLn(K),
vérifiant
GLn(K),
vérifiant
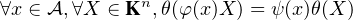

 ,Qφ(x) = ψ(x)Q. En faisant de même sur L, on conclut provisoirement
que l’hypothèse voulant que φ et ψ soient L-conjuguées suffit à garantir que les
,Qφ(x) = ψ(x)Q. En faisant de même sur L, on conclut provisoirement
que l’hypothèse voulant que φ et ψ soient L-conjuguées suffit à garantir que les  -modules ML et
NL sont isomorphes ; d’autre part il nous suffit de démontrer que les
-modules ML et
NL sont isomorphes ; d’autre part il nous suffit de démontrer que les  -modules M et N sont
isomorphes pour obtenir P
-modules M et N sont
isomorphes pour obtenir P  GLn(K) telle que ∀x
GLn(K) telle que ∀x 
 ,Pφ(x) = ψ(x)P .
,Pφ(x) = ψ(x)P .
On considère alors des décompositions M ≃ M1 ⊕ ⊕ Mp et N ≃ N1 ⊕
⊕ Mp et N ≃ N1 ⊕ Nq où
M1 , … , Mp , N1 , …,Nq sont des A-modules indécomposables. Ainsi, ML est isomorphe à la somme
directe de d copies de M1, de d copies de M2, etc, de d copies de Mp. De même, NL est isomorphe
à la somme directe de d copies de N1, de d copies de N2, etc, de d copies de Nq. Soit
W un
Nq où
M1 , … , Mp , N1 , …,Nq sont des A-modules indécomposables. Ainsi, ML est isomorphe à la somme
directe de d copies de M1, de d copies de M2, etc, de d copies de Mp. De même, NL est isomorphe
à la somme directe de d copies de N1, de d copies de N2, etc, de d copies de Nq. Soit
W un  -module indécomposable arbitraire. Notons k (respectivement kʹ) le nombre
d’indices i
-module indécomposable arbitraire. Notons k (respectivement kʹ) le nombre
d’indices i  [[1, p]] (respectivement j
[[1, p]] (respectivement j  [[1,q]]) tels que Mi (respectivement Nj) soit
isomorphe à W. Il y a donc, dans la décomposition précédente de ML (respectivement
de NL ), exactement dk (respectivement dkʹ) facteurs isomorphes à W . Le théorème
de Krull-Schmidt montre alors que dk = dkʹ, d’où k = kʹ. En faisant varier W parmi
M1 , … , Mp , N1 , …,Nq, on en déduit facilement que p = q et qu’il existe une permutation σ de
[[1, p]] telle que Mi soit isomorphe à Nσ(i) pour tout i
[[1,q]]) tels que Mi (respectivement Nj) soit
isomorphe à W. Il y a donc, dans la décomposition précédente de ML (respectivement
de NL ), exactement dk (respectivement dkʹ) facteurs isomorphes à W . Le théorème
de Krull-Schmidt montre alors que dk = dkʹ, d’où k = kʹ. En faisant varier W parmi
M1 , … , Mp , N1 , …,Nq, on en déduit facilement que p = q et qu’il existe une permutation σ de
[[1, p]] telle que Mi soit isomorphe à Nσ(i) pour tout i  [[1,p]]. partir de là, on reconstitue
sans peine un isomorphisme de
[[1,p]]. partir de là, on reconstitue
sans peine un isomorphisme de  -modules de M sur Mʹ, ce qui montre que φ et ψ sont
K-conjuguées.
-modules de M sur Mʹ, ce qui montre que φ et ψ sont
K-conjuguées.
Il y a dix ans, nous avons trouvé une démonstration inédite du lemme de Noether-Deuring pour le
cas où K est un corps fini. Pour cela, on démontre le résultat lorsque K - L est une extension
quadratique séparable arbitraire (ici on ne suppose pas K fini) : c’est clairement suffisant, puisque
qu’à partir de tout corps fini K et à l’intérieur de n’importe quel surcorps algébriquement clos de K,
on peut loger une tour d’extensions quadratiques séparables arbitrairement longue. Prenons donc
une telle extension et notons σ le K-automorphisme de L différent de l’identité. Supposons disposer
d’une matrice P  GLn(L) telle que Pψ(x) = φ(x)P pour tout x
GLn(L) telle que Pψ(x) = φ(x)P pour tout x 
 . En appliquant
l’automorphisme σ coefficient par coefficient, on voit que ∀x
. En appliquant
l’automorphisme σ coefficient par coefficient, on voit que ∀x 
 ,Pσφ(x) = ψ(x)Pσ,
donc φ(x) commute avec (Pσ)-1P pour tout x
,Pσφ(x) = ψ(x)Pσ,
donc φ(x) commute avec (Pσ)-1P pour tout x 
 . Si le commutant de (Pσ)-1P est
inclus dans celui de P , on en déduit que φ = ψ, ce qui donnerait immédiatement le
résultat voulu : l’idée de consiste à se ramener à cette situation après modification de
P.
. Si le commutant de (Pσ)-1P est
inclus dans celui de P , on en déduit que φ = ψ, ce qui donnerait immédiatement le
résultat voulu : l’idée de consiste à se ramener à cette situation après modification de
P.
Remarquons que l’on peut, pour n’importe quel couple (R,S)  GLn(K)2, remplacer φ et ψ
respectivement par x
GLn(K)2, remplacer φ et ψ
respectivement par x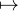 Rφ(x)R-1 et x
Rφ(x)R-1 et x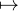 Sψ(x)S-1, ce qui a pour effet de remplacer P par
RPS-1 .
Sψ(x)S-1, ce qui a pour effet de remplacer P par
RPS-1 .
Décomposons P = A + εB où (A,B) 
 n(K)2 et ε
n(K)2 et ε  L \ K. Ce qui précède montre que
l’on peut remplacer le couple (A,B) par (RAS-1,RBS-1) pour un couple arbitraire
(R, S)
L \ K. Ce qui précède montre que
l’on peut remplacer le couple (A,B) par (RAS-1,RBS-1) pour un couple arbitraire
(R, S)  GL n (K)2 sans rien changer à notre problème. Or, les classes d’équivalences pour
l’équivalence simultanée des couples de matrices sont connues : elles relèvent de la
réduction de Kronecker-Weierstrass (voir l’annexe de pour une version simplifiée de
cette réduction). Dans la classe d’équivalence de (A,B) existe un couple particulier
(A1 , B1 ) dit réduit, et pour un tel couple on démontre que la matrice P1 := A1 + εB1
commute avec toute matrice commutant avec (P
GL n (K)2 sans rien changer à notre problème. Or, les classes d’équivalences pour
l’équivalence simultanée des couples de matrices sont connues : elles relèvent de la
réduction de Kronecker-Weierstrass (voir l’annexe de pour une version simplifiée de
cette réduction). Dans la classe d’équivalence de (A,B) existe un couple particulier
(A1 , B1 ) dit réduit, et pour un tel couple on démontre que la matrice P1 := A1 + εB1
commute avec toute matrice commutant avec (P )-1P1 (les détails sont donnés dans
).
)-1P1 (les détails sont donnés dans
).
Dans une réponse communiquée à la RMS, Jean Fresnel et Michel Matignon proposent une autre
approche, fondée sur la théorie des groupes algébriques. Nous résumerons très brièvement leur
réponse dans les lignes qui suivent. Fresnel et Matignon remarquent comme nous qu’il suffit
d’établir le résultat pour une extension algébriquement close L du corps K = Fq (où q est une
puissance d’un nombre premier) : ils se donnent donc deux listes (A1,…,Ak) et (B1,…,Bk) de
matrices de Mn (K), supposent l’existence d’une matrice P  GLn(L) telle que PAlP-1 = Bl
pour tout l de {1, …,k}, et cherchent à montrer qu’une telle matrice peut être remplacée par une
matrice de GL n (K). Pour cela, ils notent F l’automorphisme de Frobenius x
GLn(L) telle que PAlP-1 = Bl
pour tout l de {1, …,k}, et cherchent à montrer qu’une telle matrice peut être remplacée par une
matrice de GL n (K). Pour cela, ils notent F l’automorphisme de Frobenius x xq de L sur K.
Pour toute M de Mn(L), ils considèrent la matrice MF := (F(mi,j))1≤i,j≤n, ce qui définit un
automorphisme de la K-algèbre Mn(L). Pour tout l de {1,…,k}, la relation PAl = BlP donne
PF Al = Bl PF avec PF dans GLn(L). Ainsi, P-1PF commute avec chaque matrice
Al . Fresnel et Matignon introduisent alors le sous-groupe G des matrices de GLn(L)
commutant avec toutes les Al, et ils démontrent, grâce à un théorème de Serge Lang
sur les groupes algébriques affines (voir la proposition 3, page 119 de ), que la fonction
Q
xq de L sur K.
Pour toute M de Mn(L), ils considèrent la matrice MF := (F(mi,j))1≤i,j≤n, ce qui définit un
automorphisme de la K-algèbre Mn(L). Pour tout l de {1,…,k}, la relation PAl = BlP donne
PF Al = Bl PF avec PF dans GLn(L). Ainsi, P-1PF commute avec chaque matrice
Al . Fresnel et Matignon introduisent alors le sous-groupe G des matrices de GLn(L)
commutant avec toutes les Al, et ils démontrent, grâce à un théorème de Serge Lang
sur les groupes algébriques affines (voir la proposition 3, page 119 de ), que la fonction
Q  G
G Q-1 QF
Q-1 QF  G est surjective. C’est le cœur de la démonstration : il nécessite
l’introduction de la notion de sous-groupe algébrique affine, ce qui nous éloigne très
sensiblement du corpus mathématique traité habituellement dans la RMS. Ce résultat acquis, la
conclusion est aisée : on dispose alors en effet d’une matrice Q appartenant à G telle que
Q-1 QF = P-1 PF, on en tire (PQ-1)F = PQ-1, si bien que R := PQ-1 est dans GLn(K).
On obtient enfin RAlR-1 = PAlP-1 = Bl pour tout l de {1,…,k}, ce qui conclut la
démonstration.
G est surjective. C’est le cœur de la démonstration : il nécessite
l’introduction de la notion de sous-groupe algébrique affine, ce qui nous éloigne très
sensiblement du corpus mathématique traité habituellement dans la RMS. Ce résultat acquis, la
conclusion est aisée : on dispose alors en effet d’une matrice Q appartenant à G telle que
Q-1 QF = P-1 PF, on en tire (PQ-1)F = PQ-1, si bien que R := PQ-1 est dans GLn(K).
On obtient enfin RAlR-1 = PAlP-1 = Bl pour tout l de {1,…,k}, ce qui conclut la
démonstration.
Annexe : démonstration du théorème de Krull-Schmidt
Le point de départ est le lemme suivant :
Lemme 1.Soit M un  -module indécomposable de dimension finie sur K. Alors, l’ensemble
des endomorphismes non bijectifs du
-module indécomposable de dimension finie sur K. Alors, l’ensemble
des endomorphismes non bijectifs du  -module M est un idéal bilatére de End
-module M est un idéal bilatére de End (M)
(éventuellement réduit à 0) et ses élément sont tous nilpotents.
(M)
(éventuellement réduit à 0) et ses élément sont tous nilpotents.
Démonstration.Soit f un endomorphisme du  -module M. Comme endomorphisme du
K-espace vectoriel M de dimension finie, f admet une décomposition de Fitting M =
Kerfn ⊕ Im fn (où n désigne la dimension de M sur K ; on rappelle que f induit alors un
automorphisme de Imfn). Les sous-espaces vectoriels Kerfn et Imfn sont en fait des
sous-
-module M. Comme endomorphisme du
K-espace vectoriel M de dimension finie, f admet une décomposition de Fitting M =
Kerfn ⊕ Im fn (où n désigne la dimension de M sur K ; on rappelle que f induit alors un
automorphisme de Imfn). Les sous-espaces vectoriels Kerfn et Imfn sont en fait des
sous- -modules de M, donc l’indécomposabilité de f garantit que l’un d’entre eux vaut M.
Il s’ensuit que f est inversible ou nilpotent.
-modules de M, donc l’indécomposabilité de f garantit que l’un d’entre eux vaut M.
Il s’ensuit que f est inversible ou nilpotent.
Considérons ensuite l’ensemble I des éléments non-inversibles de l’anneau End (M).
Comme M est de dimension finie sur K, l’ensemble I est évidemment stable par
multiplication à gauche et à droite par les éléments de End
(M).
Comme M est de dimension finie sur K, l’ensemble I est évidemment stable par
multiplication à gauche et à droite par les éléments de End (M). Il reste à voir que I est
stable par addition. Soit u et v dans I. Supposons u+v inversible. Alors uʹ = idM-vʹ pour
uʹ := (u + v)-1 u et vʹ := (u + v)-1v, qui sont dans I. Mais alors vʹ est nilpotent, donc
idM- vʹ est inversible, ce qui contredit la non-inversibilité de uʹ. Ainsi, u + v
(M). Il reste à voir que I est
stable par addition. Soit u et v dans I. Supposons u+v inversible. Alors uʹ = idM-vʹ pour
uʹ := (u + v)-1 u et vʹ := (u + v)-1v, qui sont dans I. Mais alors vʹ est nilpotent, donc
idM- vʹ est inversible, ce qui contredit la non-inversibilité de uʹ. Ainsi, u + v  I, ce qui
achève la démonstration. __
I, ce qui
achève la démonstration. __
Par suite, le quotient de End (M) par l’idéal de ses éléments non-inversibles est un corps
(non-commutatif en général).
(M) par l’idéal de ses éléments non-inversibles est un corps
(non-commutatif en général).
Corollaire 1.Soit M et N deux modules  -indécomposables de dimension finie sur K et
non-isomorphes, et f : M → N et g : N → M deux morphismes de
-indécomposables de dimension finie sur K et
non-isomorphes, et f : M → N et g : N → M deux morphismes de  -modules. Alors g • f
est nilpotent.
-modules. Alors g • f
est nilpotent.
Démonstration.On note que g • f est un endomorphisme du  -module M et f • g un
endomorphisme du
-module M et f • g un
endomorphisme du  -module N. Il ne peuvent être tous les deux bijectifs. D’après le lemme
précédent, l’un d’entre eux est donc nilpotent, et donc classiquement l’autre aussi. __
-module N. Il ne peuvent être tous les deux bijectifs. D’après le lemme
précédent, l’un d’entre eux est donc nilpotent, et donc classiquement l’autre aussi. __
Nous sommes maintenant en mesure de démontrer le théorème de Krull-Schmidt.
Il va suffire de montrer que, pour tout  -module indécomposable M de dimension finie sur K, le
nombre de termes isomorphes à M est le même pour les deux sommes directes M1 ⊕
-module indécomposable M de dimension finie sur K, le
nombre de termes isomorphes à M est le même pour les deux sommes directes M1 ⊕ ⊕ Mp
et N1 ⊕
⊕ Mp
et N1 ⊕  ⊕ Nq. Pour cela, on se ramène facilement à la situation où l’on dispose
d’entiers d > 0 et dʹ≥ 0 tels que M = M1 =
⊕ Nq. Pour cela, on se ramène facilement à la situation où l’on dispose
d’entiers d > 0 et dʹ≥ 0 tels que M = M1 =  = Md = N1 =
= Md = N1 =  = Ne et aucun des
modules Md+1 , …,Mp,Ne+1,…,Nq n’est isomorphe à M1. Il s’agit alors de montrer que
d = e.
= Ne et aucun des
modules Md+1 , …,Mp,Ne+1,…,Nq n’est isomorphe à M1. Il s’agit alors de montrer que
d = e.
Plaçons-nous dans cette situation et prenons un isomorphisme f : M1 ⊕ ⊕Mp → N1 ⊕
⊕Mp → N1 ⊕ ⊕Nq
de
⊕Nq
de  -modules. Cet isomorphisme fournit une famille (fi,j)1≤i≤q,1≤j≤p de morphismes de
-modules. Cet isomorphisme fournit une famille (fi,j)1≤i≤q,1≤j≤p de morphismes de
 -modules, où fi,j : Mj → Ni, de sorte que f(x1,…,xp) =
-modules, où fi,j : Mj → Ni, de sorte que f(x1,…,xp) = 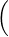
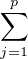 fi,j(xj)
fi,j(xj)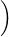 1≤i≤q pour
tout (x1 , … , xp )
1≤i≤q pour
tout (x1 , … , xp )  M1 ×
M1 × × Mp (on rappelle que M1 ⊕
× Mp (on rappelle que M1 ⊕ ⊕ Mp est vu comme le
produit cartésien des ensembles M1,…,Mp avec la structure naturelle de
⊕ Mp est vu comme le
produit cartésien des ensembles M1,…,Mp avec la structure naturelle de  -module
produit).
-module
produit).
De même, on notant g la réciproque de f, on obtient une famille (gi,j)1≤i≤p,1≤j≤q de
morphismes de  -modules, où gi,j : Nj → Mi. La relation g • f = id donne en particulier les
identités :
-modules, où gi,j : Nj → Mi. La relation g • f = id donne en particulier les
identités :
![2 ∑q {idM sii = j
∀(i,j) ∈ [[1,d]], gi,k •fk,j = 0 sinon.
k=1](/numeros/RMS130-3/RMS130-32632x.png)
 [[e + 1,q]] et tout (i,j)
[[e + 1,q]] et tout (i,j)  [[1,d]] × [[1,e]], le lemme montre que gi,k •fk,j appartient
à l’idéal I des éléments non-inversibles de End
[[1,d]] × [[1,e]], le lemme montre que gi,k •fk,j appartient
à l’idéal I des éléments non-inversibles de End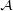 (M). En notant [u] la classe modulo I d’un
élément u de End
(M). En notant [u] la classe modulo I d’un
élément u de End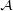 (M), les relations précédentes passent au quotient et donnent, dans le corps
gauche résiduel
(M), les relations précédentes passent au quotient et donnent, dans le corps
gauche résiduel 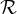 := End
:= End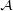 (M)⁄I, les identités
(M)⁄I, les identités
![2 ∑e
∀(i,j) ∈ [[1,d]], [gi,k][fk,j] = δi,j.1R.
k=1](/numeros/RMS130-3/RMS130-32633x.png)
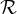 ). Il vient e ≥ d (les colonnes de A engendrent le
). Il vient e ≥ d (les colonnes de A engendrent le 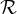 -espace vectoriel
à droite
-espace vectoriel
à droite  d , lequel est de dimension d sur
d , lequel est de dimension d sur 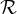 ). Symétriquement, la relation f • g = id permet
d’obtenir e ≤ d, et la conclusion s’ensuit.
). Symétriquement, la relation f • g = id permet
d’obtenir e ≤ d, et la conclusion s’ensuit.
Références
[1] C. de Seguins Pazzis, Invariance of simultaneous similarity and equivalence of matrices under extension of the ground field (en accés libre) Linear Algebra Appl. 433-3 (2010) 618–624.
[2] J.-P. Serre, Groupes algébriques et corps de classes, Hermann, Paris, 1959.
[Questions-Reponses]

