 R[X]. On suppose : e2iπP(n)
R[X]. On suppose : e2iπP(n)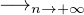 1. Montrer : ∀n
1. Montrer : ∀n  Z,
P(n)
Z,
P(n)  Z .
Z .
On raisonne par récurrence sur d = deg(P).
∙ Si deg (P) ≤ 0, alors P est constant égal à a et la suite 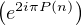 n
n N est d’une part
convergente vers 1 et d’autre part constante égale à e2iπa. Par unicité de la limite, e2iπa = 1 donc
a
N est d’une part
convergente vers 1 et d’autre part constante égale à e2iπa. Par unicité de la limite, e2iπa = 1 donc
a  Z , ce qui prouve le résultat lorsque P est constant.
Z , ce qui prouve le résultat lorsque P est constant.
∙ Soit d  N . Supposons que tout polynôme Q de degré d vérifie la propriété du texte.
N . Supposons que tout polynôme Q de degré d vérifie la propriété du texte.
Soit P  R [X] un polynôme de degré d + 1 tel que limn→+∞e2iπP(n) = 1 et considérons le
polynôme Q(X) = P(X + 1) - P(X) dont le degré est égal à d. Pour tout n
R [X] un polynôme de degré d + 1 tel que limn→+∞e2iπP(n) = 1 et considérons le
polynôme Q(X) = P(X + 1) - P(X) dont le degré est égal à d. Pour tout n  Z,
e2iπQ(n) =
Z,
e2iπQ(n) = 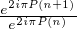 d’où limn→+∞e2iπQ(n) = 1.
d’où limn→+∞e2iπQ(n) = 1.
D’après l’hypothèse de récurrence, pour tout n  N, Q(n)
N, Q(n)  Z. Alors
Z. Alors
∀n  Z , e2iπP(n+1) = e2iπP(n), donc la suite (e2iπP(n))n
Z , e2iπP(n+1) = e2iπP(n), donc la suite (e2iπP(n))n Z est constante égale à 1, puisque
e2iπP(n)
Z est constante égale à 1, puisque
e2iπP(n) 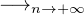 1. Il en résulte que ∀n
1. Il en résulte que ∀n  Z,P(n)
Z,P(n)  Z, ce qui établit la propriété à l’ordre
d + 1 et clôt la récurrence.
Z, ce qui établit la propriété à l’ordre
d + 1 et clôt la récurrence.
[Liste des corrigés]

