a) Montrer que les boules de E sont convexes.
b) Soit C une partie convexe de E. On suppose que C est dense dans E. Montrer que C = E : i) dans le cas où E = R ; ii) dans le cas général.
Solution d’après Lionel Ponton
a) C’est une conséquence immédiate de l’inégalité triangulaire.
b) i) Les convexes de R sont les intervalles et le seul intervalle dense dans R est R lui-même.
ii) Quitte à faire une translation, il suffit de montrer que 0  C.
C.
Soit F le sous-espace vectoriel de E engendré par C. Il est fermé (car E est de dimension finie). Alors E = C ⊂ F = F , donc F = E. Par conséquent C engendre E, donc il contient une base B = (e1 , ..., en ) de E.
Le convexe C contient l’ensemble
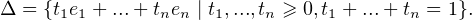
L’ensemble U = {t1e1 +  + tnen∣t1,...,tn < 0} est un ouvert non vide de E. Il rencontre
donc C : il existe x = -(x1e1 +
+ tnen∣t1,...,tn < 0} est un ouvert non vide de E. Il rencontre
donc C : il existe x = -(x1e1 +  + xnen)
+ xnen)  C ∩ U (avec x1,...,xn > 0). Posons
s = x1 +
C ∩ U (avec x1,...,xn > 0). Posons
s = x1 +  + xn. Le point y = (x1e1 +
+ xn. Le point y = (x1e1 +  + xnen)⁄s appartient à Δ donc à C.
Sachant que - 1 < 0 < 1⁄s, on en déduit que le vecteur nul de E est situé sur le segment
[x, y] ⊂ C.
+ xnen)⁄s appartient à Δ donc à C.
Sachant que - 1 < 0 < 1⁄s, on en déduit que le vecteur nul de E est situé sur le segment
[x, y] ⊂ C.
[Liste des corrigés]

