935. Soient A et B deux événements indépendants de (Ω,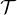 ,P). On pose Z = 1A + 1B.
,P). On pose Z = 1A + 1B.
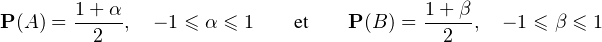
On
explicite les inégalités P(Z = k) < 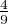 , k = 0,1,2, pour obtenir
, k = 0,1,2, pour obtenir
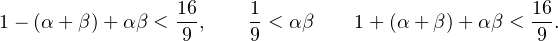
Ainsi
α et β ont même signe. Supposons sans perte de généralité que α > 0 et β > 0. Dans ce
cas
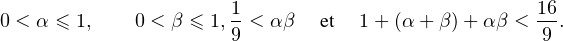
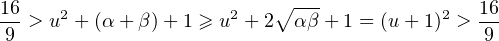
 ,P). On pose Z = 1A + 1B.
,P). On pose Z = 1A + 1B.
a) Déterminer Z(Ω).
b) Montrer qu’il existe k  Z(Ω) tel que P(Z = k) ≥ 4⁄9.
Z(Ω) tel que P(Z = k) ≥ 4⁄9.
a) On a Z(Ω) ⊂ {0,1,2}.
b) On suppose par l’absurde que P(Z = 0) < 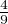 , P(Z = 1) <
, P(Z = 1) < 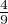 et P(Z = 2) <
et P(Z = 2) < 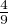 et on
pose
et on
pose
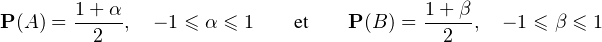
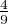 , k = 0,1,2, pour obtenir
, k = 0,1,2, pour obtenir
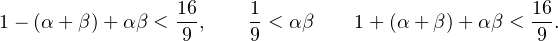
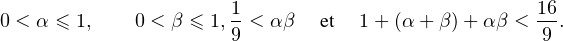
Posons u := 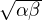 >
> 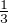 . On a
. On a
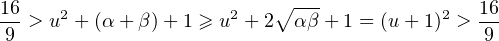
c’est absurde. Ainsi il existe k  Z(Ω) tel que P(Z = k) ≥ 4⁄9.
Z(Ω) tel que P(Z = k) ≥ 4⁄9.
Remarque. En considérant deux variables aléatoires U et V indépendantes suivant la loi 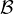
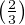 et
en posant A := (U = 1) et B := (V = 1), on constate que P(Z = 0) = 1⁄9, P(Z = 1) = 4⁄9 et
P(Z = 2) = 4⁄9 ce qui montre que la constante 4⁄9 est optimale.
et
en posant A := (U = 1) et B := (V = 1), on constate que P(Z = 0) = 1⁄9, P(Z = 1) = 4⁄9 et
P(Z = 2) = 4⁄9 ce qui montre que la constante 4⁄9 est optimale.
Solutions de Laurent Dietrich, Abdelkader Daouia, Lionel Ponton.

