n(C). On suppose qu’il existe P C[X] tel que P(A) est diagonalisable et
Pʹ(A) est inversible. Montrer que A est diagonalisable.
Solution de ric Pité
La solution ci-après est essentiellement identique à celles de Adrien Reisner, de Julien Bureaux, de Lionel Ponton et à celle obtenue conjointement par Laurent Dietrich et Simon Billouet. On indique à la fin une autre preuve du comité de la RMS mais qui a des idées communes avec celle envoyée par Ivan Gozard. Une autre méthode a été proposée par Christophe Jan, Nguyên Hai Châu et Abdelkader Daouia basée sur le lemme de décompositions des noyaux appliqué à A.
On notera que P n’est pas constant (sinon Pʹ(A) ne serait pas inversible). Notons α1,…,αp les p
valeurs propres distinctes de P(A). Ainsi, Q := 
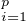(P -αi) est un polynôme annulateur de A.
L’idée est d’éliminer les facteurs multiples de Q. Supposons que l’un de ces polynômes
P - αi ait une racine multiple β. Ainsi, X - β divise Pʹ. Ce qui donne une formule
du type Pʹ = (X - β)R avec R C[X] et donc Pʹ(A) = (A - βI)R(A) ou encore
det(Pʹ(A)) = det(A - βI)det(R(A)). Par hypothèse, on comprend que A - βI est inversible
(c’est-à-dire que β n’est pas une valeur propre de A). Finalement, on peut factoriser Q = Q1Q2 où
Q2 est le produit de tous les X - β. Par construction, Q1 est scindé à racines simples
(on notera que les p polynômes P - αi n’ont aucune racine commune). Ensuite, on a
0 = Q(A) = Q1 (A)Q2(A) avec Q2(A) inversible. Autrement dit, Q1(A) = 0. Cela prouve que A
est diagonalisable.
Voici une autre solution de la RMS basée sur la notion de polynôme minimal : notons μ le
polynôme minimal de A. La diagonalisabilité de A équivaut à prouver que μ est scindé à racines
simples, ou encore que μʹ n’a aucune racine commune avec μ. Par diagonalisabilité, il existe un
polynôme Q scindé à racines simples qui annule P(A), c’est-à-dire Q(P(A)) = 0. Cela donne une
formule du type Q • P = Rμ avec R C[X]. Par dérivation et application en A, cela
donne
 |
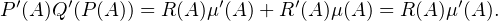Comme Q et Qʹ sont premiers entre eux, il existe une relation de Bezout de la forme S1 Q + S2 Qʹ = 1 et donc aussi entre Q • P et Qʹ• P :
 |
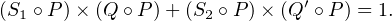En appliquant l’équation polynomiale précédente à A, on obtient que Qʹ(P(A)) est inversible. Comme Pʹ(A) est aussi inversible, on conclut que μʹ(A) est également inversible. Mais cela signifie précisément qu’aucune racine de μʹ n’est valeur propre de A, ce que l’on voulait prouver car les racines de μ sont les valeurs propres de A.