a) Déterminer la loi de X et calculer son espérance.
b) On considère Y la variable aléatoire donnant le numéro du premier tirage pour lequel on tire une boule rouge. Montrer que Y admet une espérance et calculer la loi de Y .
La modélisation proposée est celle des ≪ urnes de Polya ≫. L’énoncé ne précise pas
si la boule tirée est remise ou non dans l’urne. Nous supposons qu’elle est remise, le
problème serait le même si la boule n’était pas remise, mais que l’on rajoutait c + 1 boules
de la couleur choisie. Par ailleurs, nous noterons dans l’exercice Xn au lieu de X la
variable aléatoire qui correspond au nombre de boules rouges tirées au n-ième tirage.
Au bout de ces n tirages, il y a alors a + b + nc boules dans l’urne, dont b + Xnc sont
rouges.
Précisons aussi que l’énoncé est incorrect : Y n’admet une espérance que si b⁄c > 1.
a) Notons Rk (resp. Bk) l’événement ≪ une boule rouge (resp. blanche) est tirée au ke tirage ≫. Par
la formule des probabilités composées, la probabilité de tirer k  [ [0,n]] boules rouges en
premier, suivies de n - k boules blanches, est P(R1 ∩
[ [0,n]] boules rouges en
premier, suivies de n - k boules blanches, est P(R1 ∩ Rk ∩ Bk+1 ∩
Rk ∩ Bk+1 ∩ ∩ Bn) qui
vaut
∩ Bn) qui
vaut
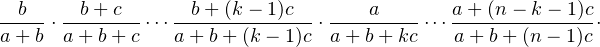
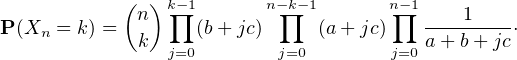
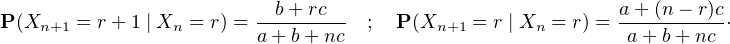
On dispose alors d’une relation sur l’espérance conditionnelle :
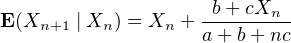
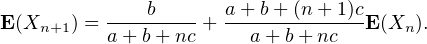
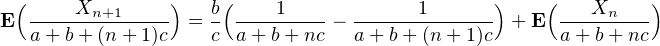
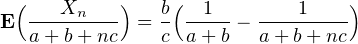
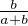 ⋅ La forme simple de ce résultat laisse penser qu’il y a peut-être une façon plus
simple de répondre à la question. En effet, si on avait a = b, alors le problème serait symétrique sur
les boules blanches et rouges, et donc la loi de Xn et celle de n-Xn serait la même, ce qui conduit
alors mécaniquement à E(Xn) =
⋅ La forme simple de ce résultat laisse penser qu’il y a peut-être une façon plus
simple de répondre à la question. En effet, si on avait a = b, alors le problème serait symétrique sur
les boules blanches et rouges, et donc la loi de Xn et celle de n-Xn serait la même, ce qui conduit
alors mécaniquement à E(Xn) = 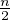 ⋅
⋅
b) Par les calculs précédents, on a
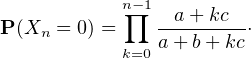
On en déduit la loi de Y : P(Y = 1) = P(X1 = 1) = 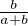 et
et
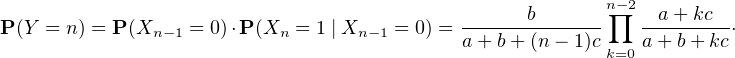
Calculons un développement asymptotique de un := P(Xn = 0) : on écrit
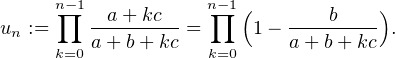
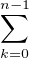 -
-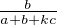 +
+ 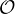 (1⁄k2) = λ-
(1⁄k2) = λ-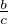 lnn +
lnn + 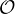 (1) après une étude classique. Ainsi, il
existe une constante A > 0 telle que
(1) après une étude classique. Ainsi, il
existe une constante A > 0 telle que
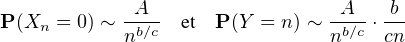
On en déduit au passage que P(Xn = 0)-→n→+∞0 et donc que Y est définie presque sûrement.
Et Y n’admet une espérance que si b⁄c > 1.
De façon complémentaire, on peut démontrer à l’aide de la relation sur l’espérance conditionnelle que la variable aléatoire
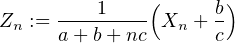
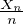 . La loi de la limite se calcule dans les cas simples : on obtient la
loi uniforme dans le cas où a = b = c = 1, et la loi bêta de paramètres a et b lorsque a et b
sont quelconques mais c = 1. Il ne serait pas choquant que dans le cas général, la loi
limite de
. La loi de la limite se calcule dans les cas simples : on obtient la
loi uniforme dans le cas où a = b = c = 1, et la loi bêta de paramètres a et b lorsque a et b
sont quelconques mais c = 1. Il ne serait pas choquant que dans le cas général, la loi
limite de 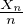 soit la loi bêta de paramètres
soit la loi bêta de paramètres 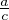 et
et 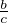 , de densité sur [0,1] proportionnelle à
xa⁄c-1 (1 - x)b⁄c-1.
, de densité sur [0,1] proportionnelle à
xa⁄c-1 (1 - x)b⁄c-1.
[Liste des corrigés]

