607. Soient n  N*, A et B dans
N*, A et B dans  n(C). On pose [A,B] = AB -BA, on suppose que A et B
commutent avec [A,B]. Pour t
n(C). On pose [A,B] = AB -BA, on suppose que A et B
commutent avec [A,B]. Pour t  R, soit f(t) = etAetBe-
R, soit f(t) = etAetBe-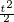 [A,B].
[A,B].
![k-1 k-∑ 1 i k- 1-i k-∑ 1( i+1 k- 1- i i k- i)
kA[A,B]= A (AB - BA )A = A BA - A BA
i=0 i=0
= AkB - BAk.](/numeros/RMS130-3/RMS130-32499x.png)
![+∞∑(k k) +∑∞ k- 1k
(tA)B- B (tA)- = kA----t[A,B ] ⇔ etAB - BetA = tetA[A, B].
k=0k! k! k=1 k!](/numeros/RMS130-3/RMS130-32500x.png)
Pour
t  R ,
R ,
![2 2 2
fʹ(t)=AetAetBe-t [A,B]⁄2 + etABetBe-t [A,B]⁄2 - etAetBt[A,B ]e-t [A,B]⁄2.](/numeros/RMS130-3/RMS130-32501x.png)
Comme A et B commutent avec [A,B], on a etAetB[A,B] = [A,B]etAetB d’où
![fʹ(t)=(A- t[A, B])etAetBe-t2[A,B]⁄2 + (BetA + t[A,B ]etA)etBe-t2[A,B ]⁄2
2
=(A+ B )etAetBe-t[A,B ]⁄2 = (A + B)f(t)](/numeros/RMS130-3/RMS130-32502x.png)
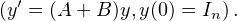
Par
unicité, f = g et, en particulier, f(1) = g(1) c’est-à-dire eA+B = eAeBe-[A,B]⁄2.
[Liste des corrigés]
 N*, A et B dans
N*, A et B dans  n(C). On pose [A,B] = AB -BA, on suppose que A et B
commutent avec [A,B]. Pour t
n(C). On pose [A,B] = AB -BA, on suppose que A et B
commutent avec [A,B]. Pour t  R, soit f(t) = etAetBe-
R, soit f(t) = etAetBe-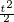 [A,B].
[A,B].
a) Pour k  N * , montrer que AkB - BAk = kAk-1[A,B].
N * , montrer que AkB - BAk = kAk-1[A,B].
b) Trouver une équation différentielle vérifiée par f.
c) Montrer que eA+B = eAeBe-![[A,B2]-](/numeros/RMS130-3/RMS130-32498x.png) .
.
Solution d’après François Capacès, Jean-Claude Jacquens, Hai Chaû Nguyên,
Adrien Reisner
a) Soit k  N * . On a :
N * . On a :
![k-1 k-∑ 1 i k- 1-i k-∑ 1( i+1 k- 1- i i k- i)
kA[A,B]= A (AB - BA )A = A BA - A BA
i=0 i=0
= AkB - BAk.](/numeros/RMS130-3/RMS130-32499x.png)
b) On déduit de a) que, pour t  R,
R,
![+∞∑(k k) +∑∞ k- 1k
(tA)B- B (tA)- = kA----t[A,B ] ⇔ etAB - BetA = tetA[A, B].
k=0k! k! k=1 k!](/numeros/RMS130-3/RMS130-32500x.png)
 R ,
R ,
![2 2 2
fʹ(t)=AetAetBe-t [A,B]⁄2 + etABetBe-t [A,B]⁄2 - etAetBt[A,B ]e-t [A,B]⁄2.](/numeros/RMS130-3/RMS130-32501x.png)
![fʹ(t)=(A- t[A, B])etAetBe-t2[A,B]⁄2 + (BetA + t[A,B ]etA)etBe-t2[A,B ]⁄2
2
=(A+ B )etAetBe-t[A,B ]⁄2 = (A + B)f(t)](/numeros/RMS130-3/RMS130-32502x.png)
c) Les applications f et g : t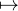 et(A+B) sont de classe
et(A+B) sont de classe 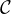 1 sur R et solutions du problème de
Cauchy
1 sur R et solutions du problème de
Cauchy
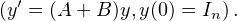
[Liste des corrigés]

