 N*, montrer que GLn(R) est dense dans
N*, montrer que GLn(R) est dense dans  n(R).
n(R).
b) Montrer que, pour n = 2 et n = 3, 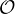 n(Q) est dense dans
n(Q) est dense dans 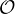 n(R). Que dire pour n
quelconque ?
n(R). Que dire pour n
quelconque ?
a) Vérifions que toute A 
 n(R) est limite d’une suite de GLn(R).
n(R) est limite d’une suite de GLn(R).
Le polynôme caractéristique de A : P = det(xIn - A) est de degré n donc il existe au plus n
valeurs de p  N * telles que A-
N * telles que A-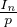
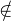 GLn(R). Prenons p0 strictement plus grand que ces valeurs
éventuelles. La suite de terme général
GLn(R). Prenons p0 strictement plus grand que ces valeurs
éventuelles. La suite de terme général 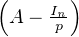 p≥p0 est une suite de GLn(R) qui tend vers
A.
p≥p0 est une suite de GLn(R) qui tend vers
A.
b) Nous admettrons le résultat classique (théorème de Cartan), fréquent sujet d’exercice, selon
lequel 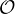 n (R ) est engendré par les matrices de réflexion. Il suffit donc de prouver que
toute matrice de réflexion est limite d’une suite de matrices de réflexion à coefficients
rationnels.
n (R ) est engendré par les matrices de réflexion. Il suffit donc de prouver que
toute matrice de réflexion est limite d’une suite de matrices de réflexion à coefficients
rationnels.
Soit H 
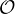 n (R ) une matrice de réflexion et h la réflexion de Rn (muni du produit scalaire usuel)
dont H est la matrice canonique. Prenons N
n (R ) une matrice de réflexion et h la réflexion de Rn (muni du produit scalaire usuel)
dont H est la matrice canonique. Prenons N  Rn un vecteur unitaire orthogonal à l’hyperplan des
invariants de h. On a alors ∀x
Rn un vecteur unitaire orthogonal à l’hyperplan des
invariants de h. On a alors ∀x  Rn,h(x) = x - 2
Rn,h(x) = x - 2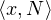 N.
N.
Considérons une suite de vecteurs non nuls Np de Qn qui tend vers N (dont l’existence découle de
la densité de Q dans R) et pour chaque p la réflexion hp d’hyperplan N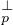 . Notons que les Np ne
sont pas forcément unitaires. On a
. Notons que les Np ne
sont pas forcément unitaires. On a
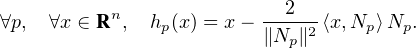
[Liste des corrigés]

