 N*, Un(C) l’ensemble des matrices M
N*, Un(C) l’ensemble des matrices M 
 n(C) telles que tMM = In.
n(C) telles que tMM = In.
a) Soit A  Un (C) symétrique. En considérant les parties réelle et imaginaire de A, montrer
que A s’écrit eiS où S
Un (C) symétrique. En considérant les parties réelle et imaginaire de A, montrer
que A s’écrit eiS où S  Sn(R). Réciproque ?
Sn(R). Réciproque ?
b) Soit A 
 n (C). Montrer que A
n (C). Montrer que A  Un(C) si et seulement si A s’écrit OeiS avec
O
Un(C) si et seulement si A s’écrit OeiS avec
O 
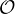 n (R ) et S
n (R ) et S  Sn(R).
Sn(R).
On vérifie immédiatement que Un(C) est un sous-groupe de GLn(C) stable par A A et A
A et A tA
et que Un (C ) ∩
tA
et que Un (C ) ∩  n(R) =
n(R) =  n(R).
n(R).
a) Soit A  Un (C) ∩
Un (C) ∩ n(C). Posons A = U + iV avec U,V
n(C). Posons A = U + iV avec U,V 
 n(R). Comme A = tA, on a
U, V
n(R). Comme A = tA, on a
U, V 
 n (R ) et
n (R ) et
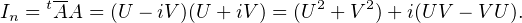
On a donc
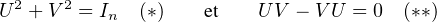
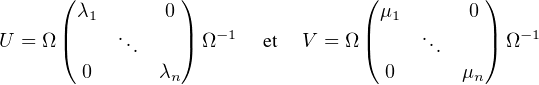
avec Ω 
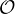 n (R ), λ1,…,λn,μ1,…,μn
n (R ), λ1,…,λn,μ1,…,μn  R.
R.
De (*) on déduit alors que λ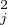 + μ
+ μ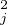 = 1 et on dispose donc de θj
= 1 et on dispose donc de θj  R tel que λj = cosθj,
μj = sin θj . On a donc
R tel que λj = cosθj,
μj = sin θj . On a donc
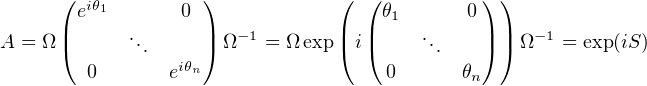
avec S = Ω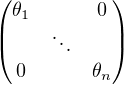 Ω-1
Ω-1

 n(R).
n(R).
Réciproquement, si S 
 n(R), il est immédiat que eiS
n(R), il est immédiat que eiS  Un(C) ∩
Un(C) ∩ n(C). Ainsi S
n(C). Ainsi S eiS induit
une surjection de
eiS induit
une surjection de  n(R) sur Un(C) ∩
n(R) sur Un(C) ∩ n(C).
n(C).
b) Soient O 
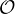 n(R) et S
n(R) et S 
 n(R). On a O
n(R). On a O  Un(C) et eiS
Un(C) et eiS  Un(C), donc OeiS
Un(C), donc OeiS  Un(C).
Un(C).
Réciproquement, soit A  Un(C). Comme tA
Un(C). Comme tA  Un(C), tAA
Un(C), tAA  Un(C). Or tAA
Un(C). Or tAA 
 n(C) et on
dispose donc selon a) de S
n(C) et on
dispose donc selon a) de S 
 n(R) telle que tAA = e2iS, d’où
n(R) telle que tAA = e2iS, d’où
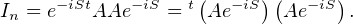
Or Ae-iS  Un (C), d’où
Un (C), d’où
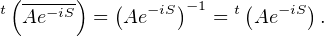
donc Ae-iS 
 n(R), soit Ae-iS
n(R), soit Ae-iS 
 n(R) ∩ Un(C) =
n(R) ∩ Un(C) = 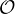 n(R).
n(R).
Posons O = Ae-iS. On a bien A = OeiS avec O 
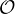 n(R) et S
n(R) et S 
 n(R).
n(R).
Ainsi, (O, S) OeiS induit une surjection de
OeiS induit une surjection de 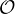 n(R) ×
n(R) × n(R) sur Un(C)
n(R) sur Un(C)

