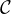 0([0,1], C), g une surjection continue croissante de [0,1] sur lui-même et Φ
l’endomorphisme de E défini par ∀f
0([0,1], C), g une surjection continue croissante de [0,1] sur lui-même et Φ
l’endomorphisme de E défini par ∀f  E, Φ(f) = f •g. Soit V un sous-espace de dimension
finie de E stable par Φ. Montrer que Φ induit un automorphisme ϕ de V dont la seule valeur
propre est 1. En déduire que ϕ = idV .
E, Φ(f) = f •g. Soit V un sous-espace de dimension
finie de E stable par Φ. Montrer que Φ induit un automorphisme ϕ de V dont la seule valeur
propre est 1. En déduire que ϕ = idV .
∙ La fonction g est surjective de [0,1] sur [0,1], on a donc
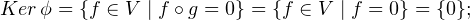
∙ Soit λ une valeur propre de ϕ et f  V \{0} un vecteur propre associé. La surjectivité de g
permet d’écrire :
V \{0} un vecteur propre associé. La surjectivité de g
permet d’écrire : 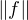 ∞ =
∞ = 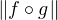 ∞ = |λ|
∞ = |λ|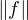 ∞, d’où |λ| = 1.
∞, d’où |λ| = 1.
Fixons un point x0  [0,1] tel que f(x0)≠0. Pour tout n
[0,1] tel que f(x0)≠0. Pour tout n  N, on a ϕn(f) = λnf, i.e. f • gn = λnf
(où gn désigne une puissance pour la loi •), en particulier f(gn(x0)) = λnf(x0). Or la fonction g
est croissante, donc la suite (gn(x0)) est monotone ; elle est aussi bornée par 0 et 1
donc elle converge vers un point fixe y de g. On en déduit que λn = f(gn(x0))⁄f(x0)
converge vers f(y)⁄f(x0). Ceci impose λ = 1 (puisque le seul complexe z de module 1
tel que la suite (zn) converge est z = 1). Ainsi la seule valeur propre possible de ϕ est
1.
N, on a ϕn(f) = λnf, i.e. f • gn = λnf
(où gn désigne une puissance pour la loi •), en particulier f(gn(x0)) = λnf(x0). Or la fonction g
est croissante, donc la suite (gn(x0)) est monotone ; elle est aussi bornée par 0 et 1
donc elle converge vers un point fixe y de g. On en déduit que λn = f(gn(x0))⁄f(x0)
converge vers f(y)⁄f(x0). Ceci impose λ = 1 (puisque le seul complexe z de module 1
tel que la suite (zn) converge est z = 1). Ainsi la seule valeur propre possible de ϕ est
1.
∙ L’espace V est un C-espace vectoriel de dimension finie donc le spectre de ϕ ne peut être vide. On en déduit que Sp(ϕ) = {1}. Considérons l’endomorphisme ψ = ϕ - idV . D’après le théorème de Cayley-Hamilton, ψ est nilpotent (car χϕ = (X - 1)dimV ). Supposons par l’absurde que son indice de nilpotence p soit > 1. On a, pour tout entier n ≥ p,
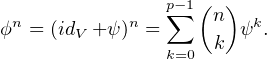
 ψp-1 et il n’est pas borné.
Plus précisément, soit f
ψp-1 et il n’est pas borné.
Plus précisément, soit f  V tel que ψp-1(f)≠0, alors on a
V tel que ψp-1(f)≠0, alors on a
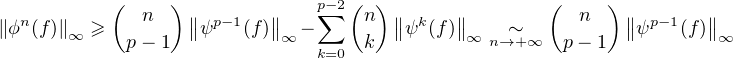
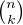 ~
~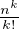 lorsque n → +∞à k fixé). On aurait donc
lorsque n → +∞à k fixé). On aurait donc 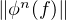 ∞→ +∞, et ceci est absurde
puisque
∞→ +∞, et ceci est absurde
puisque 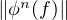 ∞ =
∞ = 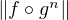 ∞ =
∞ = 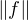 ∞ pour tout n. On conclut que p = 1, c’est-à-dire
ϕ = id V .
∞ pour tout n. On conclut que p = 1, c’est-à-dire
ϕ = id V .
Remarque. Il existe des exemples non triviaux de couples (V,g) vérifiant les hypothèses de cet
exercice. Par exemple, si K ⊂ [0,1] désigne l’ensemble triadique de Cantor, f l’escalier du diable
(fonction continue et croissante de [0,1] dans [0,1], constante sur chaque composante connexe de
cK) et g une surjection croissante telle que g(x) = x pour tout x  K et g(x) < x pour tout x
K et g(x) < x pour tout x K,
alors on a f • g = f, et V = V ect(id[0,1],f) convient. Cet exemple est non trivial au sens où
g(x)≠ x presque partout.
K,
alors on a f • g = f, et V = V ect(id[0,1],f) convient. Cet exemple est non trivial au sens où
g(x)≠ x presque partout.
[Liste des corrigés]

