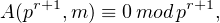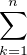7. Montrer que, si m et n sont dans N^*, n divise m^k∧n.

On note A(n, m) := 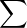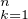m^k∧n. Nous transformerons d’abord cette somme à l’aide de la fonction ϕ d’Euler, puis montrerons une divisibilité arithmétiquement multiplicative. Nous montrerons enfin le résultat lorsque n = p^r, où p est un nombre premier.

∙ En classant les entiers k de {1,…,n} selon leur pgcd avec n, on obtient

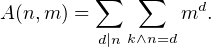
Il y a ϕ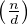 entiers k tels que k ∧ n = d. En effet, la condition précédente équivaut à d∣k et 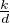∧ 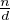= 1, donc à k = λd avec λ∧ 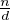= 1. Comme λ est assujetti à être inférieur ou égal à 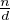, on obtient le résultat annoncé. Par suite,

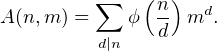
∙ Supposons n ∧ nʹ = 1. Alors

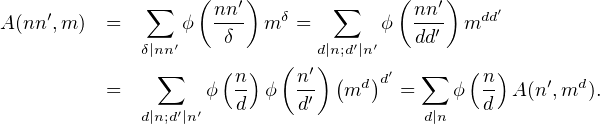
Nous avons utilisé le résultat fondamental selon lequel, si n ∧ nʹ = 1, et si D(n) désigne l’ensemble des diviseurs strictement positifs de n, alors

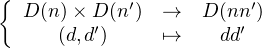
est une bijection. Nous avons en outre utilisé le fait que ϕ est arithmétiquement multiplicative.

Par conséquent, si nʹ divise toutes les quantités A(nʹ,q), alors nʹ divise A(nnʹ,m). De même, si n divise toutes les quantités A(n,r), n divise A(nnʹ,m). Par suite, nnʹ divise A(nnʹ,m). Par récurrence, il suffit de montrer que n divise A(n,m) lorsque n est de la forme p^r, où p est un nombre premier.

∙ Puisque A(p, m) = (p - 1)m + m^p,

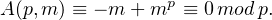
Supposons que A(p^r,m) ≡ 0modp^r et montrons que cette congruence est vraie au rang r + 1. On a

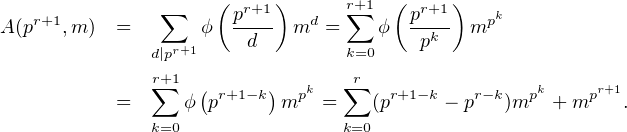
Examinons à présent deux cas.

∙ Si p∣ m, le résultat sera acquis dès lors que p^r+1 divise (p^r+1-k - p^r-k)m^pk et m^pr+1 . Concernant le dernier terme, il est divisible par p^r+1 puisque p^r+1 ≥ r + 1. En outre, p^pk divise m^pk et donc p^pk+r-k divise p^r-km^pk . Or p^k + r - k ≥ r + 1 dès que p^k - k ≥ 1, ce qui est acquis dès que k ≥ 0. Donc p^r+1 divise p^r-km^pk . A fortiori, p^r+1 divise p^r+1-km^pk .

∙ Supposons à présent que p ne divise pas m. Par l’hypothèse de récurrence,

Donc, grâce à une multiplication par p,

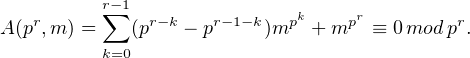
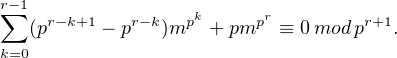
Par conséquent,

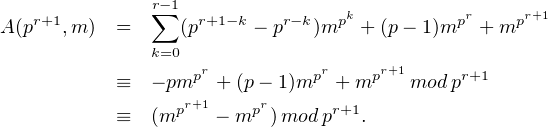
Comme m est dans le groupe des inversibles de Z⁄p^r+1Z,

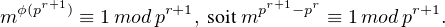
Il en résulte que m^pr+1 ≡ m^pr modp^r+1, puis que

ce qui clôt la récurrence.

[Liste des corrigés]