 N*, m
N*, m  N*, A
N*, A 
 n(C), B
n(C), B 
 m(C), C
m(C), C 
 n,m(C). Montrer que
M =
n,m(C). Montrer que
M = 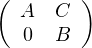 est diagonalisable si et seulement si A et B sont diagonalisables et s’il existe
X
est diagonalisable si et seulement si A et B sont diagonalisables et s’il existe
X 
 n,m (C ) tels que AX - XB = C.
n,m (C ) tels que AX - XB = C.
Solution de Adrien Joseph
Preuve du sens réciproque Supposons que A et B sont diagonalisables et que l’on dispose d’une
matrice X 
 n,m(C) telle que AX - XB = C. On montre par récurrence que pour tout
k
n,m(C) telle que AX - XB = C. On montre par récurrence que pour tout
k  N ,
N ,
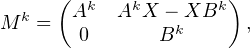
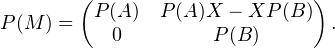 | (1) |
Considérons le polynôme P0 égal au PPCM du polynôme minimal ΠA de A et de celui ΠB de B.
Comme A et B sont diagonalisables, ΠA et ΠB sont scindés à racines simples, donc P0 l’est aussi.
D’autres part on a P0(A) = P0(B) = 0 donc P0(M) = 0. Comme P0 est scindé à racines
simples, on conclut que M est diagonalisable.
Preuve du sens direct Supposons M diagonalisable. Les caractères diagonalisables de A et B peuvent être établis par critère polynomial, mais nous allons en donner une autre preuve pour mettre C en évidence.
Par hypothèse, on dispose d’une base 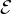 =
= 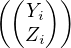 i
i [[1,n+m]] de Cn+m constituées de vecteurs
propres de M. Pour tout i, on note λi la valeur propre associée au i-ème vecteur de
[[1,n+m]] de Cn+m constituées de vecteurs
propres de M. Pour tout i, on note λi la valeur propre associée au i-ème vecteur de 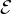 .
Ainsi :
.
Ainsi :
![∀i∈ [[1,n +m ]], AYi +CZi = λiYi et BZi = λiZi.](/numeros/RMS130-3/RMS130-32415x.png) | (2) |
On montre que la famille (Zi)i [[1,n+m]] est une famille génératrice de Cm. Pour tout
Z
[[1,n+m]] est une famille génératrice de Cm. Pour tout
Z  C m , le vecteur
C m , le vecteur 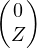 de Cn+m est combinaison linéaire des vecteurs de
de Cn+m est combinaison linéaire des vecteurs de 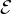 , ce qui
montre, en considérant les m dernières lignes, que Z est combinaison linéaire des vecteurs
Zi . Extrayons de la famille génératrice (Zi)i
, ce qui
montre, en considérant les m dernières lignes, que Z est combinaison linéaire des vecteurs
Zi . Extrayons de la famille génératrice (Zi)i [[1,n+m]] de Cm une base (Zj)j
[[1,n+m]] de Cm une base (Zj)j J de cet
espace.
J de cet
espace.
D’après (), on a donc exhibé une base de Cm constituée de vecteurs propres de B, ce qui montre que B est diagonalisable. En appliquant le même argument à tM, qui est diagonalisable puisque M l’est, on montre que tA est diagonalisable, donc A l’est aussi.
Considérons maintenant l’unique application linéaire f de Cm dans Cn telle que pour tout j  J,
f(Zj ) = -Y j . En notant uC (resp. uA et uB) l’application linéaire canoniquement associée à C
(resp. A et B), montrons que
J,
f(Zj ) = -Y j . En notant uC (resp. uA et uB) l’application linéaire canoniquement associée à C
(resp. A et B), montrons que
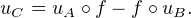 | (3) |
D’après (), pour tout j  J :
J :
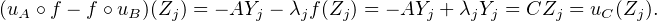

 n,m(C) la matrice de f dans les bases canoniques de Cm et de Cn, ()
donne C = AX - XB.
n,m(C) la matrice de f dans les bases canoniques de Cm et de Cn, ()
donne C = AX - XB.
[Liste des corrigés]

