496. a) Soit n 
N*. Montrer que ∀(A,t) 
n(R) × R+,det(A2 + tIn) ≥ 0.
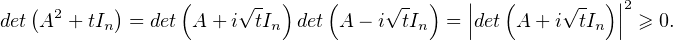
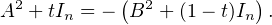
Si
- t0 ]0, 1[ n’est pas valeur propre de A2 alors A2 + t0In est inversible et
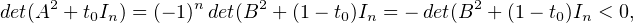
ce
qui est absurde.
[Liste des corrigés]
N*. Montrer que ∀(A,t) n(R) × R+,det(A2 + tIn) ≥ 0.
b) On suppose n N impair. Montrer que - In n’est pas somme de deux carrés de
n (R ).
Solution d’après Mohamed Houkari
a) Soient A n(R) et t R+. On a :
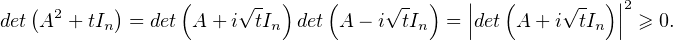
b) Soit n N impair. Supposons pas l’absurde que -In = A2 + B2 avec A,B n(R). On a,
pour tout t ]0, 1[,
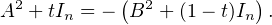
]0, 1[ n’est pas valeur propre de A2 alors A2 + t0In est inversible et
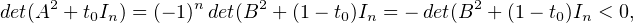
[Liste des corrigés]