 C de module
1 tel que
C de module
1 tel que 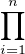 |z - ai| = 1.
|z - ai| = 1.
Remarque. L’hypothèse n ≥ 3 est inutile. Il suffit que n  N*.
N*.
Notons P le polynôme 
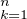 (X - ak) et écrivons P(X) =
(X - ak) et écrivons P(X) = 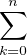 αkXk, où αn = 1 et
α0 = (-1)n a1
αkXk, où αn = 1 et
α0 = (-1)n a1  an. Alors
an. Alors
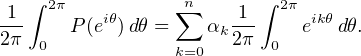
Or pour k  Z ,
Z , 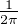
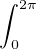 eikθ d θ = 0 si k≠0 et 1 si k = 0, donc
eikθ d θ = 0 si k≠0 et 1 si k = 0, donc
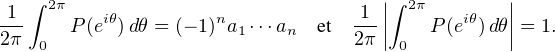
Ainsi 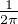
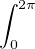
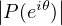 d θ ≥
d θ ≥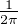
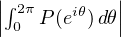 = 1.
= 1.
La fonction φ : [0,2π] → R, θ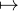
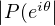 étant continue, la formule de la moyenne s’applique ; il
existe donc θ0
étant continue, la formule de la moyenne s’applique ; il
existe donc θ0  [0,2π] tel que :
[0,2π] tel que :
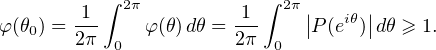
Soit θ1  [0, 2π] tel que a1 = eiθ1. Comme P(a1) = 0, φ(θ1) = 0. Le théorème des valeurs
intermédiaires appliqué à la restriction de la fonction continue φ au segment de bornes θ0 et θ1
assure qu’il existe θ (entre θ0 et θ1) tel que φ(θ) = 1. Il existe donc z
[0, 2π] tel que a1 = eiθ1. Comme P(a1) = 0, φ(θ1) = 0. Le théorème des valeurs
intermédiaires appliqué à la restriction de la fonction continue φ au segment de bornes θ0 et θ1
assure qu’il existe θ (entre θ0 et θ1) tel que φ(θ) = 1. Il existe donc z  U, à savoir z = eiθ, tel que
U, à savoir z = eiθ, tel que
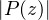 = 1.
= 1.
[Liste des corrigés]

