 N*.
N*.
a) Montrer que 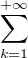
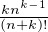 =
= 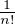 ⋅
⋅
b) Soient X1 , … , Xn des variables aléatoires i.i.d. suivant la loi de Poisson de paramètre 1. On
pose Sn = 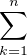 Xk et Tn =
Xk et Tn = 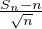 ⋅ Montrer que
⋅ Montrer que 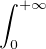 P(Tn ≥ x)d x =
P(Tn ≥ x)d x = 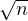
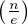 n
n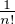 ⋅
⋅
a) On remarque que 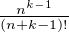 -
-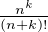 = nk-1
= nk-1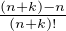 =
= 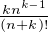 pour tout k
pour tout k  N*. Or
N*. Or 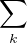
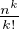 converge d’après le cours sur l’exponentielle, donc nk = ok→+∞(k!) puis nk = ok→+∞((n + k)!).
Par liaison suite-série, on conclut que
converge d’après le cours sur l’exponentielle, donc nk = ok→+∞(k!) puis nk = ok→+∞((n + k)!).
Par liaison suite-série, on conclut que
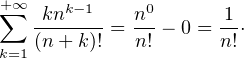
b) Commençons par établir que Sn suit la loi de Poisson 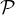 (n). D’abord on obtient que pour tout
θ
(n). D’abord on obtient que pour tout
θ  R
R 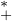 et toute variable aléatoire X suivant
et toute variable aléatoire X suivant 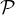 (θ),
(θ),
![+∑∞ kθk -θ tθ -θ θ(t- 1)
∀t ∈ [0,1],GX (t) = t k!e = e e = e .
k=0](/numeros/RMS130-3/RMS130-32359x.png)
 [0,1],
[0,1],
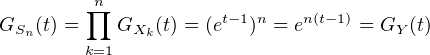
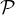 (n). La fonction génératrice déterminant la loi, on en déduit que Sn ~ Y , ce qu’il fallait
démontrer.
(n). La fonction génératrice déterminant la loi, on en déduit que Sn ~ Y , ce qu’il fallait
démontrer.
En particulier Tn est à valeurs dans n-1⁄2Z. Soit k  N. Pour tout x
N. Pour tout x 
![] k-k+1]
√n,√ n](/numeros/RMS130-3/RMS130-32361x.png) , on a donc
P(Tn ≥ x) = P
, on a donc
P(Tn ≥ x) = P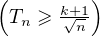 =
= 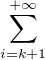 P(
P(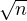 T
n = i). En particulier, x
T
n = i). En particulier, x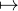 P(Tn ≥ x) est
constante sur
P(Tn ≥ x) est
constante sur ![] [
k√n, k√+n1](/numeros/RMS130-3/RMS130-32366x.png) et
et
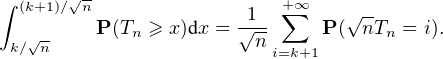
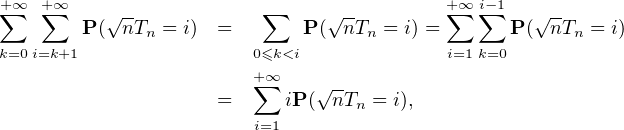
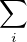 iP(
iP(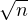 T
n = i). Or, pour tout i
T
n = i). Or, pour tout i  N*,
N*,
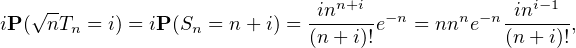
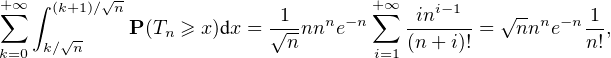
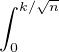 P(Tn ≥ x)dx-→
P(Tn ≥ x)dx-→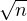 nn
e-n
nn
e-n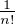 quand k tend vers + ∞.
quand k tend vers + ∞.
Ce qui précède a permis de voir que x P(Tn ≥ x) est continue par morceaux sur R+. Comme
cette fonction est positive, X
P(Tn ≥ x) est continue par morceaux sur R+. Comme
cette fonction est positive, X
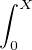 P(Tn ≥ x)dx est croissante et possède donc une limite en
+ ∞. La convergence établie plus haut montre que cette limite vaut
P(Tn ≥ x)dx est croissante et possède donc une limite en
+ ∞. La convergence établie plus haut montre que cette limite vaut 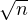 nn
e-n
nn
e-n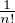 , et on conclut
que
, et on conclut
que
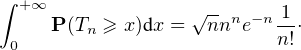
Remarque : grâce à la formule de Stirling, on voit 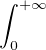 P(Tn ≥ x)dx, qui n’est autre que
E((Tn )+ ), tend vers
P(Tn ≥ x)dx, qui n’est autre que
E((Tn )+ ), tend vers 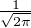 quand n tend vers + ∞. Ce résultat était prévisible par une version forte
du théorème central limite, qui donnerait que (E((Tn)+))n≥1 converge vers
quand n tend vers + ∞. Ce résultat était prévisible par une version forte
du théorème central limite, qui donnerait que (E((Tn)+))n≥1 converge vers 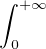 x
x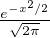 dx.
dx.

