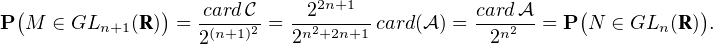N*, M une matrice aléatoire de
N*, M une matrice aléatoire de  n+1(R) dont les coefficients sont des
variables aléatoires i.i.d. suivant la loi uniforme sur {-1,1}, N une matrice aléatoire de
n+1(R) dont les coefficients sont des
variables aléatoires i.i.d. suivant la loi uniforme sur {-1,1}, N une matrice aléatoire de
 n (R ) dont les coefficients sont des variables aléatoires i.i.d. suivant la loi uniforme sur
{0, 1}. Montrer que P(M
n (R ) dont les coefficients sont des variables aléatoires i.i.d. suivant la loi uniforme sur
{0, 1}. Montrer que P(M  GLn+1(R)) = P(N
GLn+1(R)) = P(N  GLn(R)).
GLn(R)).
Solution de Jean Nougayrede
⊳ Notons 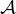 l’ensemble des matrices de GLn(R) à coefficients dans {0,2} et
l’ensemble des matrices de GLn(R) à coefficients dans {0,2} et 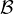 l’ensemble des
matrices de GL n+1(R) à coefficients dans {-1,1} dont la première colonne et la première ligne
sont constituées de 1. Observons que
l’ensemble des
matrices de GL n+1(R) à coefficients dans {-1,1} dont la première colonne et la première ligne
sont constituées de 1. Observons que
P N
N  GLn(R)
GLn(R)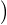 =
= 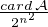 ⋅
⋅
Soit M 
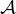 . On construit ainsi N dans
. On construit ainsi N dans 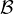 :
:
→ On commence par construire Nʹ dans Mn+1(R) par blocs :
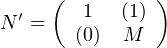
Nʹ est inversible (triangulaire par blocs avec des blocs diagonaux inversibles).
→ Ensuite, on effectue sur Nʹ les opérations élémentaires
L2 ← L1 - L2 , … ,Ln+1 ← L1 - Ln+1
pour obtenir N. Alors N est inversible car les opérations élémentaires conservent l’inversibilité.
La première colonne et la première ligne de N sont constituées de 1. Les autres coefficients de la
matrice N valent - 1 ou 1 car 1 - 2 = -1 et 1 - 0 = 1. Donc N est élément de 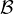 et φ : M
et φ : M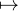 N
est une fonction bien définie de
N
est une fonction bien définie de 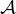 vers
vers 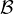 .
.
Elle est injective (comme composée des deux injections M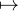 Nʹ et Nʹ
Nʹ et Nʹ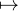 N), et elle est aussi
surjective puisque si N
N), et elle est aussi
surjective puisque si N 
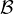 , on peut lui appliquer les mêmes opérations élémentaires
L2 ← L1 - L2 , ...Ln+1 ← L1 - Ln+1. On obtient une matrice Nʹ de la forme
, on peut lui appliquer les mêmes opérations élémentaires
L2 ← L1 - L2 , ...Ln+1 ← L1 - Ln+1. On obtient une matrice Nʹ de la forme
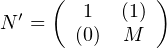
avec M 
 n (R) dont les coefficients valent 2 ou 0 (puisque 1 - 1 = 0 et 1 - (-1) = 2). De
plus, N est inversible donc Nʹ est également inversible donc M
n (R) dont les coefficients valent 2 ou 0 (puisque 1 - 1 = 0 et 1 - (-1) = 2). De
plus, N est inversible donc Nʹ est également inversible donc M  GLn(R). Finalement M
GLn(R). Finalement M 
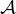 et,
par construction, φ(M) = N, ce qui démontre que φ est surjective. Ainsi,
et,
par construction, φ(M) = N, ce qui démontre que φ est surjective. Ainsi,
card(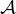 ) = card (
) = card (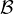 ).
).
⊳ Notons maintenant 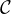 l’ensemble des matrices de GLn+1(R) à coefficients dans {-1,1} et
montrons que
l’ensemble des matrices de GLn+1(R) à coefficients dans {-1,1} et
montrons que
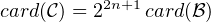
Pour cela, notons 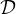 l’ensemble des matrices diagonales de
l’ensemble des matrices diagonales de  n+1(R) dont les coefficients
diagonaux sont ± 1, et
n+1(R) dont les coefficients
diagonaux sont ± 1, et 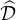 les matrices de
les matrices de 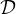 qui ont un 1 en premier coefficient. Il est clair que
card
qui ont un 1 en premier coefficient. Il est clair que
card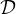 = 2n+1 et card
= 2n+1 et card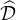 = 2n.
= 2n.
Par ailleurs, on voit que g définie sur 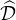 ×
×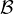 ×
× par g(D1,M,D2) = D1MD2 est bijective dans
par g(D1,M,D2) = D1MD2 est bijective dans
 , d’où le résultat voulu.
, d’où le résultat voulu.
⊳ On reprend maintenant les notations de l’énoncé et on a