 N*. On considère une famille (Xi,j)1≤i,j≤n de variables aléatoires
indépendantes suivant toutes la loi de Bernoulli de paramètre
N*. On considère une famille (Xi,j)1≤i,j≤n de variables aléatoires
indépendantes suivant toutes la loi de Bernoulli de paramètre 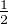 . On note A l’événement : la
matrice (Xi,j )1≤i,j≤n est inversible. Montrer que P(A) ≥
. On note A l’événement : la
matrice (Xi,j )1≤i,j≤n est inversible. Montrer que P(A) ≥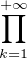
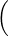 1 -
1 -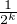
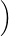 .
.
Les variables aléatoires Xi,j étant mutuellement indépendantes de même loi de Bernoulli de
paramètre 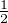 , on peut considérer Ω l’ensemble des matrices à coefficients dans
, on peut considérer Ω l’ensemble des matrices à coefficients dans 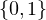 dont le
cardinal est 2n2
, muni de la tribu
dont le
cardinal est 2n2
, muni de la tribu 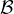 =
= 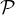 (X) et de la probabilité uniforme. Dans ce qui suit, X étant
un ensemble, on note |X| son cardinal.
(X) et de la probabilité uniforme. Dans ce qui suit, X étant
un ensemble, on note |X| son cardinal.
L’application Φ : Ω → n
n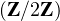 , M = (mi,j)
, M = (mi,j) M =
M = 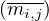 est un homomorphisme surjectif
tel que ∀M
est un homomorphisme surjectif
tel que ∀M  Ω, det
Ω, det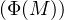 = detM. Ainsi
= detM. Ainsi
∀M  Ω, Φ(M) = M
Ω, Φ(M) = M  GLn
GLn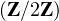
 M
M  A, donc
A, donc
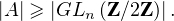
Déterminer le cardinal de GLn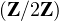 revient à compter les bases
revient à compter les bases  de
de
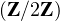 n.
n.
Remarquons d’abord que si F est un sous-espace vectoriel de 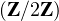 n de dimension k
n de dimension k  [ [1,n]] et
(e1 , … , ek ) est une base de F , alors |F| = 2k. En effet l’application
[ [1,n]] et
(e1 , … , ek ) est une base de F , alors |F| = 2k. En effet l’application
f : 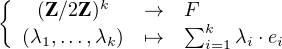 est un isomorphisme.
est un isomorphisme.
- On doit prendre v1 dans
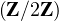 n \
n \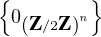 : il y a donc 2n - 1 choix.
: il y a donc 2n - 1 choix.
- Pour tout l
 [ [1,n - 1]], v1,…,vl étant choisis, il faut prendre vl+1 dans
[ [1,n - 1]], v1,…,vl étant choisis, il faut prendre vl+1 dans 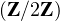 n \
Vect
n \
Vect : il y a donc 2n - 2l choix.
: il y a donc 2n - 2l choix.
Ainsi, le nombre de bases de 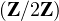 n c’est-à-dire
n c’est-à-dire 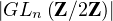 est égal à
est égal à
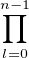
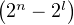 = 2n2
= 2n2
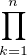
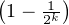 où l’on a posé : k = n - l.
où l’on a posé : k = n - l.
Donc |A| ≥ 2n2
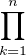
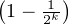 , d’où P(A) =
, d’où P(A) = 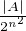 ≥
≥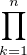
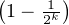 .
.
Posons pour tout n  N*, pn =
N*, pn = 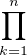
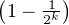 . La suite (pn)n
. La suite (pn)n N*étant positive et décroissante
converge en étant minorée par sa limite
N*étant positive et décroissante
converge en étant minorée par sa limite 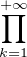
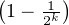 .
.
En conclusion, P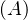 ≥
≥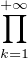
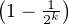 ⋅
⋅
[Liste des corrigés]

