 ,P) telle que X0 = c et, pour n
,P) telle que X0 = c et, pour n  N et x
N et x  R,
P(Xn+1 = (1 - λ)x + λ|Xn = x) = x,P(Xn+1 = (1 - λ)x|Xn = x) = 1 - x.
R,
P(Xn+1 = (1 - λ)x + λ|Xn = x) = x,P(Xn+1 = (1 - λ)x|Xn = x) = 1 - x.
a) Montrer que, si n  N, Xn est presque sûrement à valeurs dans ]0,1[ et que l’ensemble
{x
N, Xn est presque sûrement à valeurs dans ]0,1[ et que l’ensemble
{x 
![]0,1[](/numeros/RMS130-3/RMS130-32242x.png) ; P(Xn = x) > 0} est de cardinal majoré par 2n.
; P(Xn = x) > 0} est de cardinal majoré par 2n.
b) Si n  N , calculer E(Xn).
N , calculer E(Xn).
c) Montrer qu’il existe μ2 > 0 tel que ∀n  N,|E(Xn2) - c|≤ exp(-μ2n).
N,|E(Xn2) - c|≤ exp(-μ2n).
d) Soit p  N * . Montrer qu’il existe μp > 0 et mp > 0 tels que
N * . Montrer qu’il existe μp > 0 et mp > 0 tels que
∀n  N , |E(Xn p ) - c|≤ mp exp(-μpn).
N , |E(Xn p ) - c|≤ mp exp(-μpn).
e) Si t  R +* , quelle est la limite de la suite (E(tXn))n≥0 ?
R +* , quelle est la limite de la suite (E(tXn))n≥0 ?
Convergence vers une loi de Bernoulli
a) Notons V n = {x  R∣P(Xn = x) > 0}. On a V 0 = {c} et pour n
R∣P(Xn = x) > 0}. On a V 0 = {c} et pour n  N*,
N*,
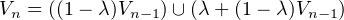
On en déduit par une récurrence immédiate que
![n
Vn ⊂ ]0,1[, Vn estfini, |Vn | ≤ 2](/numeros/RMS130-3/RMS130-32244x.png)
b) On a E(X0 ) = c et, pour n ≥ 1
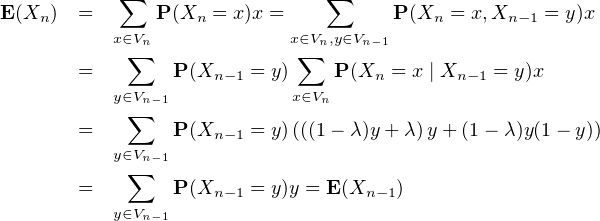
 N , E(Xn) = c.
N , E(Xn) = c.
c) Pour n ≥ 1,
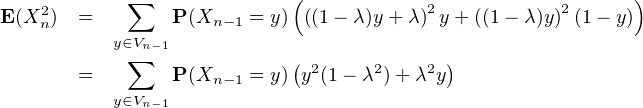
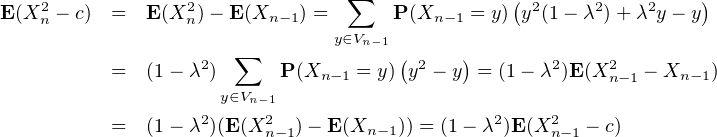
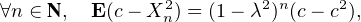
d’où l’on déduit
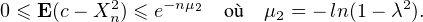
d) Soit p ≥ 2. Pour n  N, E(c - X
N, E(c - X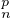 ) = E(Xn - X
) = E(Xn - X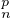 ) ≥ 0 et
) ≥ 0 et
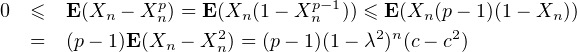
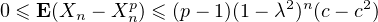
d’où l’on déduit
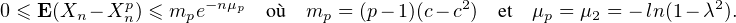
e) Soient t > 0 et p  N. On a, pour Q
N. On a, pour Q  N*
N*
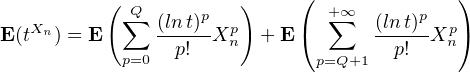
Or
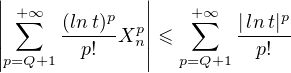
donc
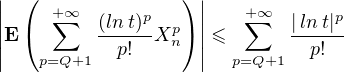
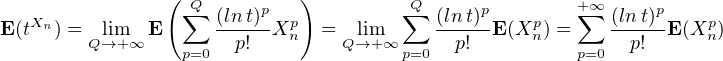
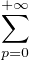
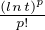 E(X
E(X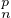 ).
).
tudions le comportement de E(tXn) lorsque n tend vers + ∞à l’aide du théorème de convergence dominée des séries. On fixe t > 0 ; quand n tend vers + ∞
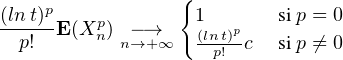
et l’on a la domination, pour p  N* et n
N* et n  N
N
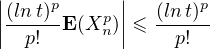
Comme 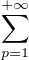
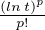 < +∞, le théorème de convergence dominée s’applique et
< +∞, le théorème de convergence dominée s’applique et
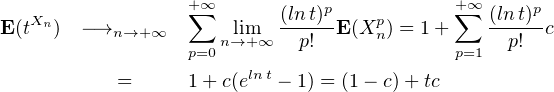
Quand n → +∞, Xn tend donc à se comporter, en un sens que nous ne tenterons pas de formaliser, comme une variable aléatoire de Bernoulli de paramètre c. Nous établissons en complément les deux résultats suivants.
Proposition 1 (loi forte). La suite (Xn) converge presque sûrement vers 0 ou 1 et l’on a
P(Xn → 1) = c et P(Xn → 0) = 1 - c
Pour alléger l’écriture, on suppose que Xn est à valeurs dans [0,1].
Première étape. Xn(1 - Xn) → 0 p.s.
Démonstration. Soit ε > 0
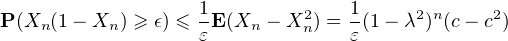
Donc 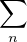 P(Xn(1 - Xn) ≤ ϵ) < +∞. On en déduit classiquement, selon Borel-Cantelli, que
Xn (1 - Xn ) → 0 p.s.
P(Xn(1 - Xn) ≤ ϵ) < +∞. On en déduit classiquement, selon Borel-Cantelli, que
Xn (1 - Xn ) → 0 p.s.
Deuxième étape. (Xn) converge p.s.
Démonstration.
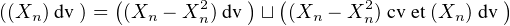
Comme (Xn - X ) converge presque sûrement vers 0, on a
) converge presque sûrement vers 0, on a
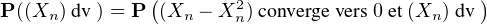
Si u  [0, 1]N , notons Λ(u) l’ensemble de ses valeurs d’adhérence. On a clairement, pour
u
[0, 1]N , notons Λ(u) l’ensemble de ses valeurs d’adhérence. On a clairement, pour
u  [0, 1]N ,
[0, 1]N ,
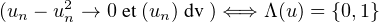
Ainsi
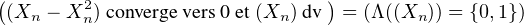
Choisissons ε0 
![] 1[
0,2](/numeros/RMS130-3/RMS130-32274x.png) tel que λ + (1 - λ)ε0 < 1 - ε0
tel que λ + (1 - λ)ε0 < 1 - ε0
On a
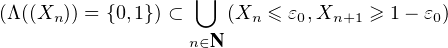
Or P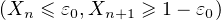 = 0, et donc P
= 0, et donc P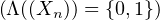 = 0 et (Xn) converge
p.s.
= 0 et (Xn) converge
p.s.
Troisième étape. L’événement 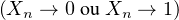 est presque certain.
est presque certain.
Démonstration. On a
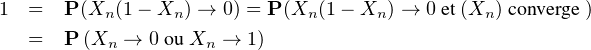
On note désormais A := (Xn → 0) et B := (Xn → 1).
Quatrième étape. Soit ε > 0. On a lorsque n → +∞,
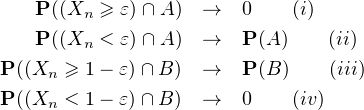
Démonstration. Prouvons (i). On a P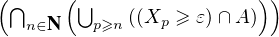 = 0, d’où
= 0, d’où
P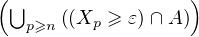 → 0
→ 0
puis P((Xn ≥ ε) ∩A) → 0. On obtient (ii) par passage au complémentaire. Les preuves de (iv) et
(iii) sont analogues à celles de (i) et (ii).
Cinquième étape. E(Xn1A) → 0 et E(Xn1B) → P(B).
Démonstration. ∙ Montrons que E(Xn1A) → 0. Soit ε > 0
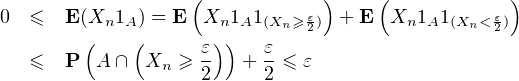
∙ Montrons que E(Xn1B) → P(B). Soit ε > 0
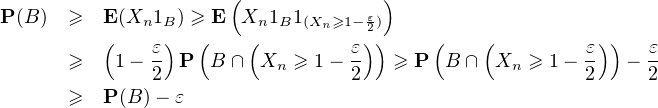
Sixième étape. Preuve de la proposition 1 (loi forte)
Démonstration.
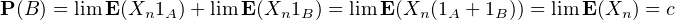
Septième étape. Preuve de la proposition 2 (loi faible)
Démonstration. Soit ε  ]0,1[.
]0,1[.
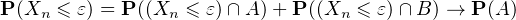
selon (i) et (iv). Donc P(Xn ≤ ε) → 1 - c.
De même
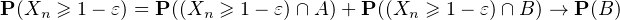
selon (ii) et (iii). Donc P(Xn ≥ 1 - ε) → c.
[Liste des corrigés]

