a) Soit z  Z tel que ∇φ(z)≠0. Que dire de Z au voisinage de z ?
Z tel que ∇φ(z)≠0. Que dire de Z au voisinage de z ?
b) On suppose que Z est compact non vide et que ∇φ ne s’annule pas sur Z. Quelle est
l’image de z  Z
Z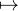
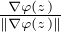 ?
?
a) On prend une base ( ,
, ) de R2 dans laquelle la seconde coordonnée de ∇φ(z) est strictement
positive. On considère d’abord le cas où z = (0,0) et (
) de R2 dans laquelle la seconde coordonnée de ∇φ(z) est strictement
positive. On considère d’abord le cas où z = (0,0) et (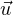 ,
,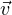 ) est la base canonique de R2. On munit
R2de la norme infinie.
) est la base canonique de R2. On munit
R2de la norme infinie.
Nous allons montrer qu’il existe deux réels rʹ > 0 et r > 0 et une fonction f : ![]](/numeros/RMS130-3/RMS130-32167x.png) -rʹ,rʹ
-rʹ,rʹ →
→![]](/numeros/RMS130-3/RMS130-32169x.png) -r,r
-r,r de
classe C1 telle que
de
classe C1 telle que
![(] [ ] [)
Z ∩ - rʹ,rʹ× - r,r = Γ f](/numeros/RMS130-3/RMS130-32171x.png) | (1) |
(théorème des fonctions implicites dans R2).
D’abord, ∂2 φ est continue et ∂2φ(0,0) > 0, donc il existe des réels r > 0 et β > 0 tels que
∂2 φ(x) ≥ β pour tout x  Bo(0,r). La fonction continue t
Bo(0,r). La fonction continue t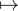 φ(0,t) est de dérivée t
φ(0,t) est de dérivée t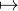 ∂2φ(0,t),
donc elle est strictement croissante sur [-r,r]. Il vient en particulier φ(0,r) > 0 et φ(0,-r) < 0.
Par continuité de φ en (0,r) et (0,-r), on trouve alors un réel rʹ
∂2φ(0,t),
donc elle est strictement croissante sur [-r,r]. Il vient en particulier φ(0,r) > 0 et φ(0,-r) < 0.
Par continuité de φ en (0,r) et (0,-r), on trouve alors un réel rʹ
![]](/numeros/RMS130-3/RMS130-32174x.png) -r,r
-r,r tel que φ(s,r) > 0 et
φ(s, -r) < 0 pour tout s
tel que φ(s,r) > 0 et
φ(s, -r) < 0 pour tout s 
![]](/numeros/RMS130-3/RMS130-32176x.png) -rʹ,rʹ
-rʹ,rʹ .
.
Fixons s 
![]](/numeros/RMS130-3/RMS130-32178x.png) -rʹ,rʹ
-rʹ,rʹ . La fonction γ : t
. La fonction γ : t  [-r,r]
[-r,r]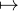 φ(s,t) est continue et strictement croissante,
avec γ(r) > 0 et γ(-r) < 0 : elle s’annule donc en un unique point de
φ(s,t) est continue et strictement croissante,
avec γ(r) > 0 et γ(-r) < 0 : elle s’annule donc en un unique point de ![]](/numeros/RMS130-3/RMS130-32181x.png) -r,r
-r,r que l’on notera
f(s). Mieux, comme γʹ est minorée par β sur
que l’on notera
f(s). Mieux, comme γʹ est minorée par β sur ![]](/numeros/RMS130-3/RMS130-32183x.png) -r,r
-r,r , l’égalité des accroissements finis montre
que |γ(f(s)) - γ(0)|≥ β|f(s) - 0|, autrement dit |f(s)|≤ β-1|φ(s,0)|.
, l’égalité des accroissements finis montre
que |γ(f(s)) - γ(0)|≥ β|f(s) - 0|, autrement dit |f(s)|≤ β-1|φ(s,0)|.
On en déduit déjà l’égalité (). En outre, comme φ(0) = 0, le développement limité de φ à l’ordre 1 en (0, 0) donne que φ(s,0) = O(s) quand s tend vers 0, donc f(s) = O(s), en particulier f est continue en 0. Pour α := ∂1φ(0) et γ := ∂2φ(0) (non nul), on a, quand s tend vers 0,
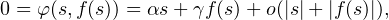
Par translation, le résultat précédent se généralise comme suit : pour tout (a,b)  Z en lequel
∂2 φ(a, b) > 0, il existe un couple (ρʹ,ρ)
Z en lequel
∂2 φ(a, b) > 0, il existe un couple (ρʹ,ρ)  (R
(R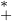 )2 et une fonction g :
)2 et une fonction g : ![]](/numeros/RMS130-3/RMS130-32187x.png) a-ρʹ,a + ρʹ
a-ρʹ,a + ρʹ →
→![]](/numeros/RMS130-3/RMS130-32189x.png) b-ρ,b + ρ
b-ρ,b + ρ dérivable en a et telle que
dérivable en a et telle que
![(] ʹ ʹ[ ] [)
Z ∩ a- ρ ,a + ρ ∩ b- ρ,b+ ρ = Γ g.](/numeros/RMS130-3/RMS130-32191x.png)

![]](/numeros/RMS130-3/RMS130-32192x.png) -rʹ,rʹ
-rʹ,rʹ et appliquons le résultat au
point (a, f(a))
et appliquons le résultat au
point (a, f(a))  Z, où l’on a effectivement ∂2φ(a,f(a)) ≥ β > 0 (on notera ρʹ,ρ,g
les objets ainsi obtenus). Remarquons ensuite que f et g coïncident au voisinage de
a : en effet d’abord (a,f(a)) = (a,g(a)) puisque (a,f(a)) est bien un point de
Z ∩
Z, où l’on a effectivement ∂2φ(a,f(a)) ≥ β > 0 (on notera ρʹ,ρ,g
les objets ainsi obtenus). Remarquons ensuite que f et g coïncident au voisinage de
a : en effet d’abord (a,f(a)) = (a,g(a)) puisque (a,f(a)) est bien un point de
Z ∩ ![(]a-ρʹ,a+ρʹ[∩ ]f(a)- ρ,f(a)+ ρ[)](/numeros/RMS130-3/RMS130-32194x.png) d’abscisse a ; ensuite, par continuité de
l’application s
d’abscisse a ; ensuite, par continuité de
l’application s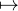 (s,g(s)) en a on voit que (s,g(s))
(s,g(s)) en a on voit que (s,g(s)) 
![]](/numeros/RMS130-3/RMS130-32196x.png) -rʹ,rʹ
-rʹ,rʹ ×
×![]](/numeros/RMS130-3/RMS130-32198x.png) -r,r
-r,r pour s voisin de a,
donc g(s) = f(s) pour s voisin de a. Comme g est dérivable en a, on conclut que f l’est
aussi.
pour s voisin de a,
donc g(s) = f(s) pour s voisin de a. Comme g est dérivable en a, on conclut que f l’est
aussi.
Ainsi, f est dérivable. Par dérivation de la fonction composée x φ(x,f(x)), on obtient
alors
φ(x,f(x)), on obtient
alors
![] ʹ ʹ[ ʹ
∀x ∈ - r,r ,∂1φ(x,f(x)) + f(x)∂2φ(x,f(x )) = 0](/numeros/RMS130-3/RMS130-32201x.png)
![∀x∈ ]- rʹ,rʹ[,fʹ(x) = - (∂1φ(x,f(x)))(∂2φ(x,f(x)))-1.](/numeros/RMS130-3/RMS130-32202x.png)
Revenons au cas général : en utilisant l’isomorphisme affine (s,t) z + s
z + s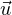 + t
+ t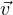 , on se
ramène à la situation précédente pour obtenir deux réels rʹ > 0 et r > 0 et une fonction
f :
, on se
ramène à la situation précédente pour obtenir deux réels rʹ > 0 et r > 0 et une fonction
f : ![]](/numeros/RMS130-3/RMS130-32206x.png) -rʹ,rʹ
-rʹ,rʹ →
→![]](/numeros/RMS130-3/RMS130-32208x.png) -r,r
-r,r de classe C1 telle que
de classe C1 telle que
![{ ] ʹ ʹ[ ] [} { ] ʹ ʹ[}
Z∩z+s⃗u+t⃗v | (s,t) ∈ - r,r × - r,r = z + s⃗u + f(s)⃗v | s ∈ - r ,r .](/numeros/RMS130-3/RMS130-32210x.png) | (2) |
Plus grossièrement, il existe un voisinage de z dont l’intersection avec Z est le support d’un arc régulier de classe C1.
b) Nous donnons une solution indépendante de la question précédente.
Pour tout z  Z le vecteur Ψ(z) :=
Z le vecteur Ψ(z) := 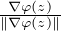 est évidemment unitaire. Réciproquement,
donnons-nous un vecteur unitaire
est évidemment unitaire. Réciproquement,
donnons-nous un vecteur unitaire 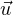 de R2 et montrons qu’il existe un point z de Z tel que
Ψ(z) =
de R2 et montrons qu’il existe un point z de Z tel que
Ψ(z) = 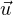 .
.
Nous introduisons la forme linéaire θ : x  R2
R2 (
(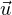 ∣x). Elle est continue, donc sur le compact non
vide Z elle admet un maximum M et un minimum m. En particulier, φ ne s’annule sur aucun des
ensembles
∣x). Elle est continue, donc sur le compact non
vide Z elle admet un maximum M et un minimum m. En particulier, φ ne s’annule sur aucun des
ensembles
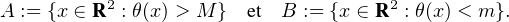
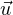 en une base orthonormée (
en une base orthonormée (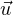 ,
,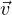 ) de R2 : le compact Z est borné pour la
norme infinie N dans cette base, d’où un réel R > 0 tel que ∀x
) de R2 : le compact Z est borné pour la
norme infinie N dans cette base, d’où un réel R > 0 tel que ∀x  Z,N(x) < R. Le
segment délimité par (m - 1)
Z,N(x) < R. Le
segment délimité par (m - 1)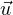 + R
+ R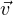 et (M + 1)
et (M + 1)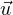 + R
+ R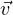 ne rencontre donc pas Z, et a ses
extrémités respectivement dans B et A. Une nouvelle application du théorème des valeurs
intermédiaires montre que φ a même signe en ces extrémités, et ainsi φ est de signe constant sur
A ∪ B.
ne rencontre donc pas Z, et a ses
extrémités respectivement dans B et A. Une nouvelle application du théorème des valeurs
intermédiaires montre que φ a même signe en ces extrémités, et ainsi φ est de signe constant sur
A ∪ B.
Nous introduisons maintenant des points a et b de Z tels que θ(a) = M et θ(b) = m.
- Supposons d’abord que φ(z) ≥ 0 pour tout z
 A∪B. Montrons que φ est positive sur
C := {x
A∪B. Montrons que φ est positive sur
C := {x  R2 : θ(x) ≥ M}. Soit x
R2 : θ(x) ≥ M}. Soit x  C. Pour tout t
C. Pour tout t  R
R on a θ(x + t
on a θ(x + t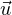 ) > M donc
φ(x + t
) > M donc
φ(x + t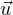 ) ≥ 0 ; en faisant tendre t vers 0 on trouve donc φ(x) ≥ 0 par continuité de
φ.
) ≥ 0 ; en faisant tendre t vers 0 on trouve donc φ(x) ≥ 0 par continuité de
φ.
Soit ensuite
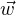
 R2 tel que θ(
R2 tel que θ(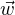 ) ≥ 0. Pour tout t
) ≥ 0. Pour tout t  R
R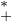 on a θ(a + t
on a θ(a + t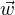 ) ≥ θ(a) = M,
donc
) ≥ θ(a) = M,
donc
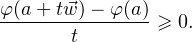
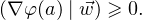
(3) Si en outre
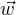 ⊥
⊥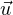 alors cette inégalité s’applique aussi à -
alors cette inégalité s’applique aussi à -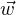 et montre que ∇φ(a)⊥
et montre que ∇φ(a)⊥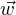 . Ainsi,
par double orthogonalité ∇φ(a) = λ
. Ainsi,
par double orthogonalité ∇φ(a) = λ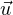 pour un réel λ (nécessairement non nul). Si λ < 0 on
obtiendrait une contradiction en appliquant () à
pour un réel λ (nécessairement non nul). Si λ < 0 on
obtiendrait une contradiction en appliquant () à 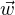 := -∇φ(a). Ainsi λ > 0 puis
Ψ(a) =
:= -∇φ(a). Ainsi λ > 0 puis
Ψ(a) = 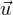 .
.
- Supposons ensuite que φ(z) ≤ 0 pour tout z
 A∪B. Alors le cas précédent s’applique au
couple (-φ,-
A∪B. Alors le cas précédent s’applique au
couple (-φ,-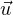 ), ce qui donne Ψ(b) =
), ce qui donne Ψ(b) = 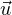 .
.
En conclusion, l’image de Ψ est l’ensemble des vecteurs unitaires de (R2,∥-∥).

