a) Montrer que G est isomorphe au groupe des matrices de la forme 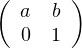 où
(a, b)
où
(a, b)  C * × C .
C * × C .
b) Pour g  G, on note (ag,bg) l’unique couple de complexes tel que g : z
G, on note (ag,bg) l’unique couple de complexes tel que g : z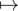 agz + bg. À quelle
condition sur (ag ,bg) l’application g admet-elle un unique point fixe ?
agz + bg. À quelle
condition sur (ag ,bg) l’application g admet-elle un unique point fixe ?
c) Soit (g1 , g2 , g3)  G3. On pose h = g
G3. On pose h = g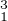 g
g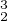 g
g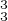 . Calculer ah et bh en fonction des agi et
bgi .
. Calculer ah et bh en fonction des agi et
bgi .
d) On admet que si ag1ag2ag3 = j et si ag1,ag2,ag3 sont tous distincts de j, alors
bh = -j2 a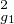 ag2 (ag1 - j)(ag2 - j)(ag3 - j)(α + βj + γj2),
ag2 (ag1 - j)(ag2 - j)(ag3 - j)(α + βj + γj2),
où α, β, γ désignent les points fixes respectifs de g2g3, g3g1 et g1g2.
On se donne un triangle direct ABC du plan complexe. On note respectivement a,b,c les
mesures principales des angles orientés (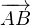 ,
,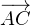 ), (
), (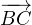 ,
,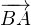 ) et (
) et (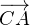 ,
,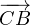 ). On note α
l’unique point tel que
). On note α
l’unique point tel que 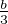 soit une mesure de (
soit une mesure de (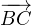 ,
,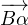 ) et
) et 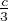 soit une mesure de (
soit une mesure de (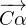 ,
,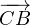 ) ; β
l’unique point tel que
) ; β
l’unique point tel que 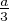 soit une mesure de (
soit une mesure de (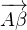 ,
,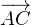 ) et
) et 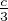 soit une mesure de (
soit une mesure de (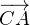 ,
,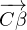 ) ;
γ l’unique point tel que
) ;
γ l’unique point tel que 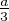 soit une mesure de (
soit une mesure de (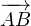 ,
,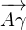 ) et
) et 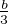 soit une mesure de
(
soit une mesure de
(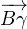 ,
,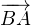 ).
Montrer que le triangle αβγ est équilatéral. On appliquera ce qui précède en prenant pour g1
(resp. g2 , g3 ) la rotation de centre A (resp. B, C) et d’angle de mesure
).
Montrer que le triangle αβγ est équilatéral. On appliquera ce qui précède en prenant pour g1
(resp. g2 , g3 ) la rotation de centre A (resp. B, C) et d’angle de mesure 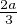 (resp.
(resp.
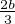 ,
, 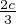 ).
).
a) Tout élément de G est une application de C dans C de la forme z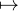 az + b où (a,b)
az + b où (a,b)  C*× C.
Notons H l’ensemble des matrices de la forme
C*× C.
Notons H l’ensemble des matrices de la forme 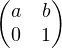 où (a,b)
où (a,b)  C*× C et ϕ l’application de G
dans H associant à g : z
C*× C et ϕ l’application de G
dans H associant à g : z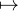 az + b la matrice Ag =
az + b la matrice Ag = 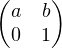 . L’application ϕ est clairement une
bijection. Soient g,h
. L’application ϕ est clairement une
bijection. Soient g,h  G et a,α
G et a,α  C*, b,β
C*, b,β  C tels que :
C tels que :
∀z  C , g(z) = az + b et h(z) = αz + β. On a (en écrivant gh pour g • h),
C , g(z) = az + b et h(z) = αz + β. On a (en écrivant gh pour g • h),
gh : z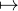 a(αz + β) + b = (aα)z + aβ + b, donc gh est associée au couple
a(αz + β) + b = (aα)z + aβ + b, donc gh est associée au couple 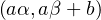 ,
,
et 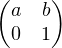
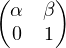 =
= 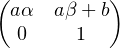 , donc ϕ(gh) = ϕ(g)ϕ(h). Il en résulte que (H,.) est un
groupe isomorphe à (G,.).
, donc ϕ(gh) = ϕ(g)ϕ(h). Il en résulte que (H,.) est un
groupe isomorphe à (G,.).
b) Soit z  C ; z est un point fixe de g si et seulement si agz + bb = z, ce qui équivaut à
(1 - ag )z = bg .
C ; z est un point fixe de g si et seulement si agz + bb = z, ce qui équivaut à
(1 - ag )z = bg .
Si ag ≠ 1, g a pour unique point fixe le point 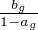 ⋅
⋅
Si ag = 1 et bg ≠ 0, g n’a pas de point fixe.
Si ag = 1 et bg = 0, g = idC et g possède une infinité de points fixes.
Donc g possède un unique point fixe si et seulement si ag≠1.
c) On a 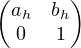 =
= 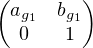 3
3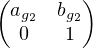 3
3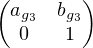 3. En effectuant les produits de
matrices, on obtient :
3. En effectuant les produits de
matrices, on obtient :
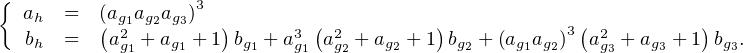
Le j dont il est fait référence dans cette question est évidemment e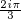 ⋅
⋅
Supposons que ag1ag2ag3 = j et ag1,ag2,ag3 tous distincts de j, alors ag2g3 = ag2ag3≠1, ag3 g1 = ag3 ag1 ≠ 1 et ag1g2 = ag1ag2≠1 et d’après b), g2g3, g3g1 et g1g2 possède chacun un unique point fixe noté respectivement α,β,γ. De plus,
bh = -j2 a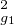 ag2 (ag1 - j)(ag2 - j)(ag3 - j)(α + βj + γj2).
ag2 (ag1 - j)(ag2 - j)(ag3 - j)(α + βj + γj2).
La vérification de cette formule (que le texte invite à admettre) est directe quoiqu’un peu lourde et repose sur les remarques : j = ag1ag2ag3 , j3 = 1, 1 + j + j2 = 0
et 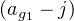
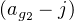
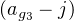 = j
= j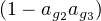
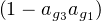
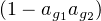 .
.
Les deux assertions suivantes sont équivalentes :
- g
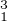 g
g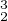 g
g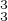 = idC.
= idC.
- α + βj + γj2 = 0.
En effet, si g1 , g2 ,g3 vérifient i), bh = 0 et il résulte des hypothèses que le facteur de bh,
- j2 a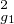 ag2 (ag1 - j)(ag2 - j)(ag3 - j) est non nul, donc α + βj + γj2 = 0, ce qui prouve
ii).
ag2 (ag1 - j)(ag2 - j)(ag3 - j) est non nul, donc α + βj + γj2 = 0, ce qui prouve
ii).
Réciproquement, supposons l’énoncé ii) vérifié. Alors bh = 0, et comme ah = j3 = 1, h = idC, ce qui prouve i).
Dans ce qui suit, on confond tout point du plan complexe avec son affixe et toute transformation du
plan avec l’application de C dans C associée. Ici g1 (resp. g2,g3) est la rotation de centre A (resp.
B, C) et d’angle de mesure 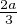 (resp.
(resp. 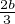 ,
,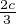 ). Rappelons qu’une rotation du plan complexe est
associée à une application affine g : C → C, z
). Rappelons qu’une rotation du plan complexe est
associée à une application affine g : C → C, z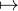 αz + β où α
αz + β où α  U et β
U et β  C. Notons s1,s2,s3 les
réflexions d’axes respectifs (BC), CA) et (AB).
C. Notons s1,s2,s3 les
réflexions d’axes respectifs (BC), CA) et (AB).
g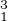 est la rotation de centre A d’angle de mesure 2a, donc g1 = s2s3 et de même g
est la rotation de centre A d’angle de mesure 2a, donc g1 = s2s3 et de même g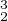 = s3s1,
g
= s3s1,
g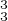 = s1 s2 . Alors g
= s1 s2 . Alors g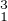 g
g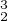 g
g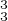 = s2s3s3s1s1s2 = idC. De plus, g1g2g3 est un déplacement d’angle
= s2s3s3s1s1s2 = idC. De plus, g1g2g3 est un déplacement d’angle
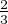 (a + b + c) =
(a + b + c) = 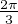 , donc ag1ag2ag3 = j. Les applications g1g2, g2g3 et g3g1 sont des déplacements
dont l’angle a une mesure principale appartenant à
, donc ag1ag2ag3 = j. Les applications g1g2, g2g3 et g3g1 sont des déplacements
dont l’angle a une mesure principale appartenant à ![] [
0, 2π3-](/numeros/RMS130-3/RMS130-32159x.png) , donc ag1,ag2,ag3 sont tous distincts de
j.
, donc ag1,ag2,ag3 sont tous distincts de
j.
Notons sBα et sCα les réflexions d’axes respectifs (Bα) et (Cα) et remarquons que g2 = sBαs1 et g3 = s1 sCα . Alors g2g3 = sBαs1s1sCα = sBαsCα, donc g2g3 a pour point invariant α (ce point est unique). De même g3g1 a pour unique point fixe β et g1g2 a pour unique point fixe γ. L’équivalence entre i) et ii) montre que α + βj + γj2 = 0, ce qui indique que le triangle αβγ est équilatéral de sens direct.
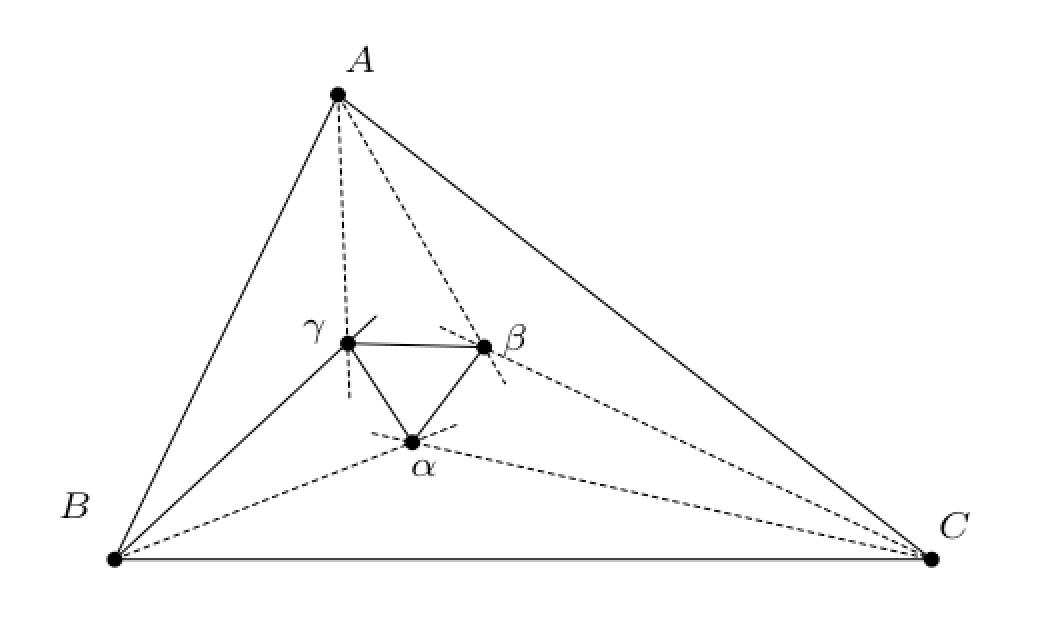
Remarque. Le résultat géométrique obtenu en d) est le théorème de Morley (1898).
La démonstration de ce théorème proposée dans l’exercice s’inspire de l’article d’Alain Connes, A
new proof of Morley’s theorem, Publications mathématiques de l’I.H.É.S, tome S88 (1998), p.
43-46. Cette démonstration très algébrique étudiant le groupe des transformations affines de la
droite permet d’étendre le résultat à tout corps (commutatif) de caractéristique différente de
3.
[Liste des corrigés]

