 N*, il existe (p,q) de
Z× [[1, n]] tel que
N*, il existe (p,q) de
Z× [[1, n]] tel que 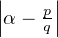 <
< 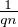 .
.
b) Soit d  N * . On suppose que d n’est pas un carré parfait.
N * . On suppose que d n’est pas un carré parfait.
Montrer que l’équation a2 - db2 = 1 possède une solution (a,b)  Z2 telle que
b≠ 0.
Z2 telle que
b≠ 0.
Nous proposons une rédaction unifiée mais les arguments sont essentiellement identiques à ceux de Ivan Gozard, Christophe Jan, Adrien Reisner, François Capacès, Lionel Ponton et Noé Weeks.
a) C’est la version la plus simple du théorème d’approximation de Dirichlet et sa démonstration
repose sur le principe des tiroirs. Notons D : R → [0,1[ la fonction partie décimale. Par irrationalité
de α, les n + 1 nombres D(α),…,D(nα),D((n + 1)α) sont distincts et appartiennent à [0,1[. Si
l’on découpe [0, 1[ en n intervalles 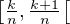 avec k
avec k  {0,1,…,n- 1} alors on peut affirmer qu’il
existe deux nombres distincts, disons D(lα) et D(lʹα) avec l < lʹ qui appartiennent au
même intervalle. En particulier, on a |D(lα) - D(lʹα)| <
{0,1,…,n- 1} alors on peut affirmer qu’il
existe deux nombres distincts, disons D(lα) et D(lʹα) avec l < lʹ qui appartiennent au
même intervalle. En particulier, on a |D(lα) - D(lʹα)| < 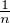 . En posant q = lʹ- l, on a
q
. En posant q = lʹ- l, on a
q  {1, … , n} et |qα - p| <
{1, … , n} et |qα - p| < 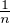 pour un bon choix de p découlant d’un calcul de partie
entière.
pour un bon choix de p découlant d’un calcul de partie
entière.
b) Il s’agit de l’équation de Pell-Fermat. La question est difficile et n’attendait évidemment pas
une réponse immédiate. L’hypothèse sur d assure que 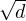 est irrationnel. Examinons
les couples (p, q)
est irrationnel. Examinons
les couples (p, q)  Z × N⋆ de la question précédente pour α =
Z × N⋆ de la question précédente pour α = 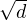 . En faisant tendre
n vers + ∞ dans la question précédente, on voit que l’on a inf (p,q)
. En faisant tendre
n vers + ∞ dans la question précédente, on voit que l’on a inf (p,q)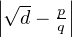 = 0.
Cela prouve manifestement que l’ensemble des nombres
= 0.
Cela prouve manifestement que l’ensemble des nombres 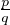 est infini (lorsque n décrit
N⋆).
est infini (lorsque n décrit
N⋆).
La condition 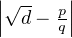 <
< 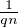 ≤
≤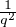 implique de plus
implique de plus
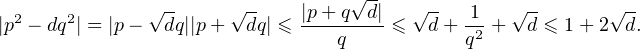 |
Autrement dit, les nombres p2 - dq2 sont uniformément bornés.
Remarquons maintenant que les nombres p2 - dq2 sont entiers. Comme l’ensemble des couples
(p, q) est infini, on déduit du point précédent qu’il existe un nombre K  Z (vérifiant
|K| ≤ 1 + 2
Z (vérifiant
|K| ≤ 1 + 2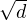 ) tel que l’ensemble suivant soit également infini
) tel que l’ensemble suivant soit également infini
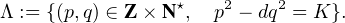 |
L’irrationalité de 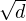 exclut K = 0. Il nous reste à atteindre le cas K = 1. Si K est un carré tel que
exclut K = 0. Il nous reste à atteindre le cas K = 1. Si K est un carré tel que
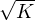 divise p et q, alors c’est fini car il suffit de choisir (a,b) =
divise p et q, alors c’est fini car il suffit de choisir (a,b) = 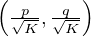 . Expliquons
comment nous ramener, plus ou moins, à cette situation. Pour obtenir de la divisibilité par
K, on exploite le caractère infini de (p⁄q)(p,q)
. Expliquons
comment nous ramener, plus ou moins, à cette situation. Pour obtenir de la divisibilité par
K, on exploite le caractère infini de (p⁄q)(p,q) Λ et la finitude de (Z⁄KZ)2. Ainsi, on
a
Λ et la finitude de (Z⁄KZ)2. Ainsi, on
a
![∃(p,q) ⁄= (pʹ,qʹ) ∈ Λ p ≡ pʹ[K ] et q ≡ qʹ[K ].](/numeros/RMS130-3/RMS130-3334x.png) |
Comme remarqué ci-dessus, on peut de plus supposer 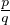 ≠
≠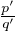 . On invoque maintenant une astuce de
théorie algébrique des nombres : il s’avère que la fonction (p,q)
. On invoque maintenant une astuce de
théorie algébrique des nombres : il s’avère que la fonction (p,q)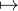 p2 - dq2, analogue à
(p, q)
p2 - dq2, analogue à
(p, q)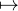 p2 + q2 , est multiplicative en munissant l’ensemble des couples (p,q) de la
structure d’anneau héritée de R en identifiant (p,q) et p + q
p2 + q2 , est multiplicative en munissant l’ensemble des couples (p,q) de la
structure d’anneau héritée de R en identifiant (p,q) et p + q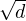 . Autrement dit, si l’on
écrit
. Autrement dit, si l’on
écrit
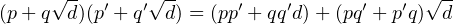 |
alors on vérifie que l’on a
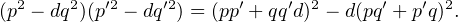 |
Cette identité, appelée l’identité de Brahmagupta, généralise l’identité bien connue du cas d = -1. Pour atteindre notre conclusion, on invoque la forme équivalente de cette identité en remplaçant q par - q :
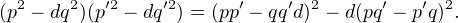 |
Sous cette forme, on peut écrire
![22 ʹ2 ʹ2 ʹ ʹ 2 2 ʹ ʹ
p-dq=K,p - dq = K, pp - qq d ≡ p - q d = K [K ], pq - p q ≡ 0 [K].](/numeros/RMS130-3/RMS130-3343x.png) |
Finalement le couple d’entiers suivant convient
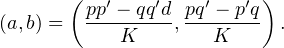 |
Notons que b≠ 0 car 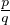 ≠
≠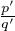 .
.

