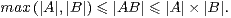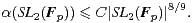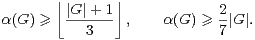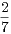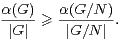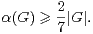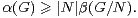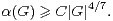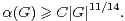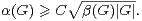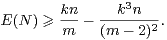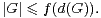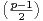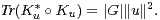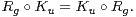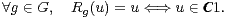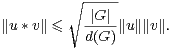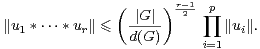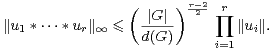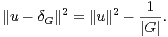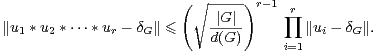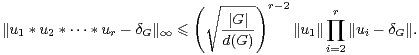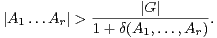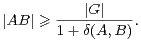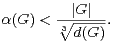[Table des matières]
Groupes quasi aléatoires
par Nicolas Tosel
Lycée Louis-le-Grand, Paris
Résumé. Ce texte est une version détaillée d’un exposé donné le 3 Juin 2016, lors d’une journée en l’honneur de Bernard Randé. Son but essentiel est de présenter la notion de groupe quasi aléatoire, introduite par Gowers en 2007. Afin de motiver la discussion, nous partons d’un problème de théorie des groupes finis d’énoncé élémentaire, l’estimation du cardinal maximal d’une partie absolument instable. Une partie des résultats démontrés est présente dans le sujet 0 de l’agrégation docteurs (problème 1, en ligne).
Abstract. Quasirandom groups
This text is the elaborate version of a conference given on June 3rd, 2016, during a day in honour of Bernard Randé. Its main goal is to present the notion of quasirandom group, introduced by Gowers in 2007. In order to inspire the discussion, we begin with a elementary problem from the theory of finite groups, the estimate of the size of the largest product-free subset. Some of these results can be found in the test subject of the ≪agrégation docteurs ≫ (problem 1, on line).
Mots-clés : groupes finis, représentations, parties absolument instables, groupes quasi-aléatoires.
1.Introduction, notations et rappels
Dans tout ce texte, (G,.) désigne un groupe fini non nul de neutre e. Si r est dans N* et si A1,…,Ar sont des parties non vides de G, on pose
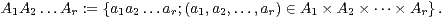
Une partie non vide X de G est dite absolument instable1 1. En anglais : product-free. si (XX) ∩ X = ∅, i.e. si
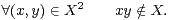
On note α(G) le cardinal maximal d’une partie absolument instable de G. Les premiers résultats relatifs à α(G) sont dus à Babai et Sòs ([2]). Ces auteurs ont prouvé que, si G a un quotient abélien non nul :
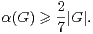
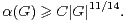
Ces résultats conduisent aux questions suivantes, dont la première remonte à [2] et la seconde à [7].
- Existe-t-il une constante C > 0 telle que, pour tout G, on ait
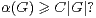
- Sinon, est-il vrai que, pour tout élément ε de ]0,1[, il existe Cε > 0 tel que, pour tout G :
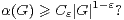
En 2007, Gowers a démontré le théorème suivant ([4]), qui infirme la seconde conjecture, donc, a fortiori, la première.
Ces résultats appartiennent à la version non commutative de la ≪ combinatoire additive ≫ 2 . Ils constituent un fil conducteur de ce texte, dont le but essentiel est cependant de présenter la notion de groupe quasi aléatoire3 , introduite par Gowers dans [4]. La rédaction doit beaucoup aux articles originaux, mais aussi aux livres [8] et [10]. On ne fait ici qu’effleurer le sujet. Le lecteur désireux d’approfondir la notion de groupe quasi aléatoire trouvera dans le chapitre 3 de [10] une discussion plus approfondie ; cette référence et l’article [5] inscrivent le sujet dans la thématique récente des ≪ groupes approximatifs ≫ .
La section 2 est consacrée aux minorations de α(G). La suite du texte (sections 3 à 5) est centrée sur la notion de groupe quasi aléatoire. On y établit des propriétés d’≪ expansion ≫ dont le théorème 1 est un simple corollaire.
Le prérequis est limité aux notions de base sur les groupes et les représentations4 . Dans la section 2, une conséquence de la classification des groupes finis simples joue un rôle de boîte noire. Le texte est complété par quelques exercices.
Nous terminons cette introduction par quelques rappels.
Le groupe dérivé de G est le sous-groupe de G engendré par les commutateurs ghg-1h-1 pour (g, h) dans G2 ; on le note D(G). Rappelons que D(G) est un sous-groupe normal (c’est-à-dire distingué) du groupe G, que le quotient G⁄D(G), appelé abélianisé de G, est le plus grand quotient abélien de G. Précisément, si H est un sous-groupe normal de G tel que G⁄H soit abélien, alors H contient D(G) et G⁄H est donc isomorphe à un quotient de l’abélianisé de G.
Le groupe G est dit parfait s’il n’a pas de quotient abélien non trivial, soit G = D(G). Si G n’est pas parfait, G a un quotient cyclique non nul.
Le groupe G est dit simple s’il est non nul et n’a pas de sous-groupe normal autre que lui-même et le sous-groupe nul. Les groupes simples et abéliens sont les groupes (cycliques) d’ordre premier. On montre facilement que tout groupe fini non nul admet un quotient simple (considérer un sous-groupe normal strict de G de cardinal maximal, donc maximal au sens de l’inclusion).
Exercice 2.a) Vérifier qu’un groupe simple de cardinal non premier est parfait.
b) Vérifier que tout quotient d’un groupe parfait est parfait.
c) Soit p un nombre premier ≤ 5. Justifier que SL2(Fp) est parfait non simple.
2.1.Le cas où G n’est pas parfait
Commençons par un exemple simple.
Démonstration On peut supposer que G est le groupe Z⁄nZ où n ≥ 2. Posons
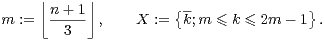
cqfd
Démonstration L’image réciproque d’une partie absolument instable X de G⁄N par la surjection canonique est une partie absolument instable de G de cardinal |X||N|. cqfd
Démonstration L’hypothèse entraîne que G a un quotient cyclique non nul. Les lemmes 1 et 2 entraînent le résultat. cqfd
Cet énoncé s’applique aux groupes abéliens, plus généralement aux groupes
résolubles5 ,
mais également à d’autres familles, par exemple aux groupes symétriques 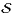 n.
n.
Dans le cas abélien, la valeur exacte de α(G) a été déterminée par Green et Rusza ([6]).
Exercice 4.a) Vérifier que, pour tout G :
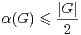
b) On suppose que G est cyclique et que l’ensemble des diviseurs premiers congrus à 2 modulo 3 de |G| n’est pas vide et on note p le plus petit élément de cet ensemble. Montrer6
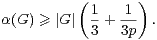
2.2.Première minoration de α(G) dans le cas général
On part d’une remarque très simple de Babai et Sòs ([2]).
Lemme 3.Soient H un sous-groupe de G autre que G, g dans G \ H. Alors gH est une partie absolument instable de G.
Démonstration Il suffit de noter que, pour h,hʹ,hʹʹ dans H,
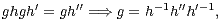
Notons donc β(G) le cardinal maximal d’un sous-groupe de G autre que G. On déduit des lemmes 2 et 3 une nouvelle minoration de α(G). cqfd
Selon [7], la classification des groupes finis simples fournit une constante K > 0 telle que, pour tout groupe fini simple G de cardinal non premier, on ait7
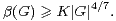
On en déduit le théorème suivant, dont le principe de la démonstration remonte à [2].
Démonstration Soit N un sous-groupe normal de G autre que G tel que que G⁄N soit simple. Si G⁄N n’est pas de cardinal premier, on a
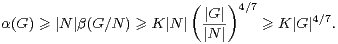
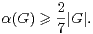
Le but de ce paragraphe est de démontrer l’amélioration suivante du théorème 2, obtenue par Kedlaya dans [7].
Pour démontrer le théorème 4, il suffit de combiner la minoration de β(G) présentée dans le paragraphe précédent au théorème 5 ci-après.
Appliqué à des groupes spécifiques, le théorème 5 donne des résultats meilleurs que le théorème 4.
Exemple Grandes parties absolument instables de SL2(Fp)
Si p est un nombre premier, le groupe G = SL2(Fp) est de cardinal p3 - p ; le sous-groupe des matrices triangulaires supérieures de déterminant 1, de cardinal p2 - p, en est un sous-groupe strict. On obtient donc l’existence d’une constante C > 0 telle que, pour tout p premier
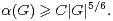
La démonstration du théorème 5 est une généralisation de celle du théorème 3. Précisément, Kedlaya remplacé la classe à droite modulo un sous-groupe de cardinal maximal utilisée par Babai et Sòs dans le lemme 2 par une réunion de telles classes. L’observation de base est que, si n = |G|, se donner un sous-groupe de cardinal n⁄m de G revient à se donner une action transitive de G sur un ensemble de cardinal m.
Lemme 5.Soit m ≥ 2 un entier. Supposons que G agisse transitivement sur {1,…,m}, notons

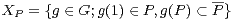
Démonstration Soient g et gʹ dans XP. Alors g(1) est dans P , donc gʹg(1) n’est pas dans P , donc l’élément gʹg n’est pas dans XP.
Le lemme 5 conduit à choisir P de sorte que |XP| soit aussi grand que possible. Pour ce faire, on
utilise la méthode probabiliste. On considère une variable aléatoire P suivant la loi uniforme sur
l’ensemble 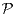 k des parties de cardinal k de {2,…,m} et on désigne par N la variable aléatoire
donnant le cardinal de P :
k des parties de cardinal k de {2,…,m} et on désigne par N la variable aléatoire
donnant le cardinal de P :
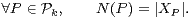
Démonstration du théorème 5 Prenons
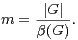
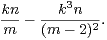
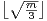 , ce qui permet de minorer le
minorant, au moins pour m assez grand, par
, ce qui permet de minorer le
minorant, au moins pour m assez grand, par
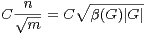
Démonstration du lemme 6 On écrit
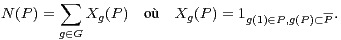
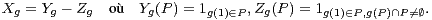
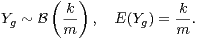
On écrit alors :
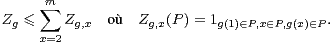
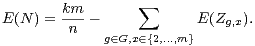
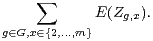
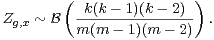
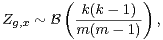
La transitivité de l’action fait que, pour x fixé, le nombre de g de G tels que g(x) = 1 (resp. g.x = x) est n⁄m. On arrive ainsi à la majoration suivante, à partir de laquelle il est aisé de conclure :
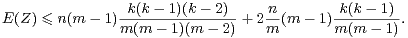
Par représentation, on entend ici ≪ représentation dans un espace vectoriel complexe de dimension finie ≫ : une représentation de G est donc un morphisme de G dans un groupe GL(E) où E est un C-espace vectoriel de dimension finie, ou, de façon équivalente, dans un groupe GLn(C). Le degré d’une telle représentation est la dimension de E.
Les groupes finis apparaissent souvent à travers leurs représentations. Inversement, la théorie des représentations donne de puissants outils pour étudier les groupes finis. Un exemple célèbre est le théorème de Burnside garantissant la résolubilité d’un groupe dont l’ordre a au plus deux facteurs premiers ([8]). Les résultats présentés dans la suite relient le degré minimal d’une représentation non triviale de G, noté d(G), à des propriétés combinatoires de G.
Soit d un élément de N*. Selon Gowers ([4]), le groupe G est dit d-quasi aléatoire8 si
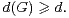
La terminologie n’est pas d’emblée transparente. Gowers l’introduit à partir d’une notion analogue en théorie des graphes (≪ graphes quasi aléatoires ≫), le lien s’effectuant via la notion de graphe de Cayley. Nous en verrons une autre explication dans le paragraphe 5.2.
Exemples et remarques
- 1.
- Si G est abélien, d(G) = 1 : l’image d’un tel groupe par une représentation est en effet codiagonalisable.
- 2.
- Pour n ≥ 2, soit Sn le groupe symétrique sur {1,…,n}. Alors d(
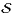 n) = 1 : la signature
donne en effet une représentation non triviale de degré 1.
n) = 1 : la signature
donne en effet une représentation non triviale de degré 1.
- 3.
- On peut unifier les exemples 1 et 2 et caractériser les groupes 2-quasi aléatoires. Les
représentations de degré 1 de G sont en effet naturellement en bijection avec celles
de l’abélianisé de G. Or, un groupe abélien fini de cardinal m admet exactement m
caractères, c’est-à-dire exactement m classes de représentation de degré 1. Il s’ensuit
que
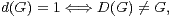
- 4.
- Soit N un sous-groupe normal de G autre que G. Comme une représentation de G⁄N
se relève en une représentation de G, on a
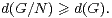
- 5.
- Soit H un sous-groupe strict de G. En considérant la représentation de G déduite de
l’action sur G⁄H par translation, on obtient :
![d(G ) ≤ [G : H].](/numeros/RMS127-4/RMS127-491x.png)
![d(G) ≤ [G : H ]- 1.](/numeros/RMS127-4/RMS127-492x.png)
- 6.
- On ne définit donc pas vraiment de notion de groupe quasi aléatoire. Informellement,
un groupe présente un comportement quasi aléatoire si d(G) est grand. Pour fixer les
idées, disons qu’une suite (Gk)k≥1 de groupes finis est quasi aléatoire si
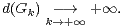
La suite (
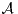 n)n≥2 des groupes alternés est quasi aléatoire. La théorie des représentations
du groupe symétrique9
montre en effet que, pour n ≥ 6 :
n)n≥2 des groupes alternés est quasi aléatoire. La théorie des représentations
du groupe symétrique9
montre en effet que, pour n ≥ 6 :
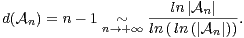
- 7.
- Rappelons un résultat fondamental de Jordan, dont on trouvera une preuve dans [1].
Théorème 6. Il existe une fonction f de N* dans N* telle que tout sous-groupe fini de GLn(C ) contienne un sous-groupe abélien normal d’indice majoré par f(n).
Notons désormais f(n) le minimum des entiers m de N* tel que tout sous-groupe fini de GLn(C ) contienne un sous-groupe abélien normal d’indice majoré par m. Le théorème de Jordan entraîne aussitôt le résultat ci-après, qui montre que la famille des groupes simples non cycliques est quasi aléatoire.
Démonstration Il suffit de combiner le fait qu’une représentation non triviale de G est fidèle au fait que le seul sous-groupe abélien normal de G est {e}, d’indice |G|10 . cqfd
Il résulte de cet énoncé et du calcul de d(
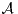 n) que, quand le cardinal du groupe simple G tend
vers + ∞ :
n) que, quand le cardinal du groupe simple G tend
vers + ∞ :
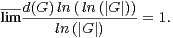
Exercice 5.Soit N un sous-groupe normal de G. Montrer que, si N et G⁄N sont d-quasi aléatoires, il en est de même de G.
Exercice 6.On suppose que G est engendré par ∪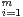 Gi où les Gi sont des sous-groupes
stricts non nuls de G. Montrer
Gi où les Gi sont des sous-groupes
stricts non nuls de G. Montrer
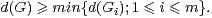
L’exercice ci-après utilise une des relations fondamentales de la théorie de Frobenius-Schur.
Exercice 7.Soit γ(G) le nombre de classes de conjugaison de G. Montrer que, pour tout G :
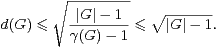
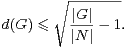
Exercice 8.Soit d dans N*. On suppose que G est parfait et que tout sous-groupe normal de G autre que G est d’indice strictement supérieur à f(d - 1). Montrer que G est d- quasi aléatoire.
Nous aurons besoin dans la suite d’un résultat classique de Frobenius.
Démonstration Définissons, pour x dans Fp, les matrices de SL2(Fp) :
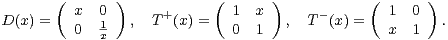
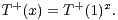
Soit ρ une représentation de degré n de SL2(Fp), à valeurs dans GLn(C). On suppose à présent que T+ (1) est dans le noyau de ρ. Alors, pour x dans Fp, le noyau de ρ contient
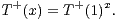
On suppose ρ non triviale. D’après ce qui précède, la matrice ρ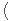 T+(1)
T+(1)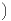 est un élément d’ordre p
de GL n (C ). Elle est donc diagonalisable à valeurs propres dans Up et l’une de ses valeurs propres,
disons λ, est différente de 1.
est un élément d’ordre p
de GL n (C ). Elle est donc diagonalisable à valeurs propres dans Up et l’une de ses valeurs propres,
disons λ, est différente de 1.
On utilise alors la formule :
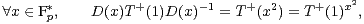
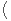 T+(1)
T+(1)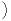 . Or, il y a
. Or, il y a
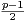 carrés dans F
carrés dans F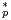 . On obtient ainsi que ρ
. On obtient ainsi que ρ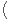 T+(1)
T+(1)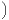 admet au moins
admet au moins 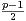 valeurs propres distinctes,
ce qui entraîne
valeurs propres distinctes,
ce qui entraîne
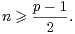
Pour la suite, le point clé est l’existence d’une constante C > 0 telle que :
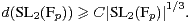
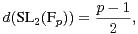
Exercice 9.En considérant l’action naturelle de SL2(Fp) sur l’espace projectif et la représentation de permutation associée, ainsi que la fin de la remarque 5 du paragraphe 3.1, montrer
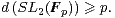
Exercice 10.Soient p un nombre premier impair, r un élément de N*, q = pr, n ≥ 2 un entier. Justifier les inégalités :
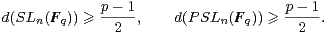
Landazuri et Seitz ont généralisé le lemme de Frobenius et déterminé le comportement asymptotique de d(G) lorsque G appartient à une des séries de groupes simples finis. On renvoie à [3] pour les résultats (sans démonstration) et la référence à l’article original.
4.1.Algèbre de groupe et opérateurs de convolution
On note C [G] l’espace vectoriel des fonctions de G dans C. On munit C[G] du produit scalaire
hermitien 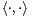 défini par
défini par
![∀(u,v) ∈ C [G ]2 ⟨u,v⟩ := ∑ u(g)v(g).
g∈G](/numeros/RMS127-4/RMS127-4123x.png)
La norme associée à ce produit scalaire est notée ⋅ : pour u dans C[G], on a donc
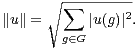
Pour u dans C [G], on pose aussi
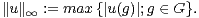
Si u et v sont dans C[G], leur produit de convolution est l’élément u * v de C[G] défini par
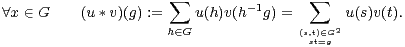
Pour u dans C [G], l’opérateur de convolution 12 associé à u est l’endomorphisme Ku de C[G] défini par
![∀w ∈ C[G] Ku(w) := u *w.](/numeros/RMS127-4/RMS127-4127x.png)
Les lemmes de ce paragraphe sont de simples vérifications laissées au lecteur. Le premier montre que l’adjoint d’un opérateur de convolution est un opérateur de convolution.
Lemme 7.Pour u dans C[G], l’adjoint de Ku est l’endomorphisme Kũ où ũ est la fonction de G dans C définie par
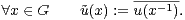
On note C 0 [G] le sous-espace de C[G] constitué des fonctions u telles que
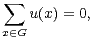
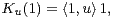
Exercice 11.Vérifier que l’application
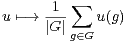
Soit R la représentation de permutation de G associée à l’action à droite de G sur lui-même :
![∀g ∈ G ∀f ∈ C[G ] ∀x ∈ G, Lg(f)(x ) = f(xg).](/numeros/RMS127-4/RMS127-4134x.png)
Pour u et v dans C[G], on a les inégalités immédiates
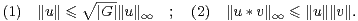
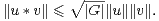
Ces inégalités ne peuvent pas être améliorées sans hypothèse supplémentaire, comme on le voit en prenant u = v = 1.
L’inégalité de mélange est un raffinement de la précédente, valable lorsque l’une des deux fonctions u, v appartient à C0[G]. Elle a été découverte par Babai, Nikolov et Pyber dans leur travail [3], inspiré de Gowers. On suit ici la présentation de Tao ([10]).
Démonstration du théorème 9 Soit u dans C0[G], non nul. Nous souhaitons démontrer que la
norme d’opérateur de Ku sur l’espace hermitien (C[G],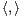 ) est majorée par
) est majorée par
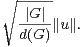
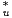 •Ku. Soit λ cette valeur propre
maximale. Puisque u n’est pas la fonction nulle, les opérateurs Ku et K
•Ku. Soit λ cette valeur propre
maximale. Puisque u n’est pas la fonction nulle, les opérateurs Ku et K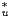 • Ku sont non nuls et λ
est dans R +* .
• Ku sont non nuls et λ
est dans R +* .
Les lemmes 7 et 9 entraînent que tous les Rg stabilisent les espaces propres de K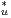 • Ku. On
obtient ainsi une représentation de G dans Ker(K
• Ku. On
obtient ainsi une représentation de G dans Ker(K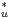 • Ku - λId). Puisque Ku s’annule sur les
constantes, le lemme 10 entraîne que cette représentation n’est pas triviale.
• Ku - λId). Puisque Ku s’annule sur les
constantes, le lemme 10 entraîne que cette représentation n’est pas triviale.
On a donc
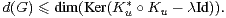
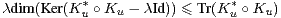
L’inégalité de mélange s’étend, via une récurrence immédiate, en l’énoncé suivant.
En utilisant l’inégalité (2), on déduit du corollaire 2 une majoration en norme uniforme.
L’exercice ci-après, vivement recommandé, anticipe sur la section suivante.
Exercice 12.a) Soient A,B,C trois parties non vides de G. Montrer
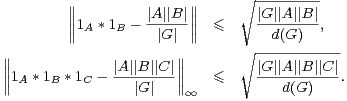
b) En déduire
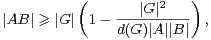
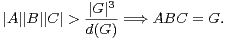
c) Conclure que
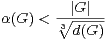
5.Applications de l’inégalité de mélange
Nous suivons ici l’article [3] de Babai, Nikolov et Pyber, qui généralise des résultats de Gowers ([4]). L’idée directrice est d’appliquer l’inégalité de mélange à des distributions de probabilité sur G. On obtient par ce moyen des résultats meilleurs que ceux de l’exercice 12.
5.1.Distributions de probabilités sur G
Le support d’un élément u de C[G] est l’ensemble
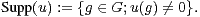
Soit  (G) l’ensemble des distributions de probabilité sur G, c’est-à-dire des fonctions u de G dans
R+telles que
(G) l’ensemble des distributions de probabilité sur G, c’est-à-dire des fonctions u de G dans
R+telles que
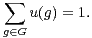
Lemme 11.Soient r un élément de N*, u1,…,ur dans C[G]. Pour i dans {1,…,p}, soit
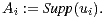
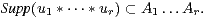
 (G).
(G).
Démonstration Le premier point est immédiat. Pour le second, on note que, pour (a1,…,ar) dans
A1 ×  × Ar ,
× Ar ,
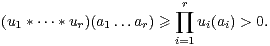
Remarque Convolution et produit de variables aléatoires à valeurs dans G.
La convolution des distributions de probabilité apparaît naturellement lors de l’étude des marches
aléatoires sur G, via l’observation suivante, dont la vérification est immédiate. Soient r un élément
de N * , X1 , … , Xr des variables aléatoires à valeurs dans G, mutuellement indépendantes et de
distributions respectives u1,…,ur. Alors la distribution de probabilité de la variable aléatoire
X1 … Xr est u1 *  * ur.
* ur.
Si A est une partie non vide de G, soit δA =  la distribution de probabilité uniforme sur A. La
distribution uniforme sur G est donc
la distribution de probabilité uniforme sur A. La
distribution uniforme sur G est donc
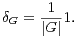
Deux observations très simples vont nous permettre d’exploiter l’inégalité de mélange.
Démonstration Le résultat découle du théorème de Pythagore et de la décomposition orthogonale
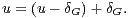
Lemme 13.Soit A une partie non vide de G. Alors, si u est un élément de  (G) à support
contenu dans A
(G) à support
contenu dans A
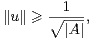
Démonstration L’inégalité se déduit de l’inégalité de Cauchy & Schwarz :
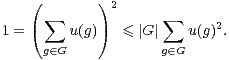
5.2.Distance d’une convolée de distributions de probabilité à la loi uniforme et théorèmes d’expansion
Commençons par appliquer les corollaires 2 et 3 aux distributions de probabilité.
Démonstration Compte-tenu des corollaires 2 et 3, il suffit de noter que, si u et v sont dans
 (G) :
(G) :
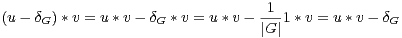
Nous sommes maintenant en mesure de démontrer les résultats essentiels de [3]. Si A1,…,Ap sont des parties non vides de G, soit :
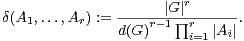
Démonstration Le support de la distribution de probabilité δA1 * * δAr est exactement
A1 A2 … Ar . Les lemmes 12, 13 et la première partie du théorème 9 entraînent
* δAr est exactement
A1 A2 … Ar . Les lemmes 12, 13 et la première partie du théorème 9 entraînent
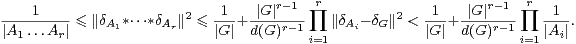
Le cas r = 2 du théorème 10 mérite un énoncé séparé.
L’exercice 12 donne l’inégalité plus faible

Pour r = 2, le second volet de l’énoncé suivant est dû à Gowers ([4]) et le premier à Nikolov et Pyber ([9]). On trouve dans [5] une démonstration utilisant l’analyse de Fourier sur G.
Théorème 11.Soient r ≥ 2 un entier, A1,…,Ar des parties non vides de G. Supposons
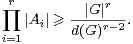
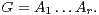
 × Ar tel que
× Ar tel que
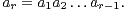
Démonstration Les lemmes 12 et 13 donnent :
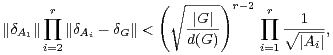
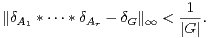
 * δAr ne s’annule pas, ce qui établit le résultat souhaité.
* δAr ne s’annule pas, ce qui établit le résultat souhaité.
Appliquons maintenant le premier point aux parties A1,…Ar-1 et Ar-1. Il vient que e s’écrit
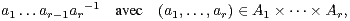
En prenant r = 3 et A1 = A2 = A3 = A dans le théorème 11, on obtient le résultat ci-après, dû à Gowers ([4]).
Pour conclure, montrons, toujours d’après [3], que, si la condition du théorème 11 est
satisfaite de façon forte, les éléments de G sont représentés comme produits a1…ap avec
(a1 , … , ap )  A1 ×
A1 × × Ap de manière presque uniforme, ce qui donne une justification à la
terminologie ≪ quasi aléatoire ≫.
× Ap de manière presque uniforme, ce qui donne une justification à la
terminologie ≪ quasi aléatoire ≫.
Théorème 12.Soient r ≥ 2 un entier, α un élément de R+*, A1,…,Ar des parties non vides de G. Supposons
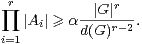
 × Ar tels que
× Ar tels que
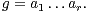
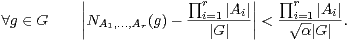
Démonstration Pour g dans G :
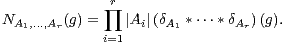
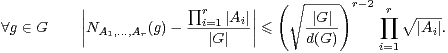
Démonstration du théorème 1
Pour G = SL 2 (F p), le majorant fourni par le corollaire 5 est équivalent, lorsque p tend vers + ∞, à
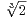 p8⁄3, c’est-à-dire à
p8⁄3, c’est-à-dire à 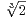 |SL2(Fp)|8⁄9. cqfd
|SL2(Fp)|8⁄9. cqfd
Cardinal de AB lorsque A et B sont deux ≪grandes ≫ parties de SL2(Fp)
Soient G = SL 2 (Fp), A une partie non vide de G. Nous allons déduire du corollaire 4 que, si |A| dépasse un certain seuil, alors |AA| est considérablement plus grand que |A|.
Le sous-groupe de G constitué des matrices triangulaires supérieures de G est de cardinal p2 - p. Le seuil se situe donc au-delà de p2.
Si C est un élément de R+* et si |A|≥ Cp5⁄2, alors
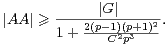
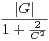 .
.
L’expansion commence en fait pour des valeurs plus faibles de |A|. En effet, si C est un élément de
R+*, δ un élément de ]0,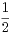 [ et si |A|≥ Cp2+δ, alors
[ et si |A|≥ Cp2+δ, alors
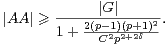
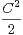 p2+2δ. Ces résultats ont servi de
motivation aux auteurs de [3]. On les comparera avec celui de l’exemple du paragraphe 2.3, avec
lequel ils contrastent dans une certaine mesure.
p2+2δ. Ces résultats ont servi de
motivation aux auteurs de [3]. On les comparera avec celui de l’exemple du paragraphe 2.3, avec
lequel ils contrastent dans une certaine mesure.
Les minorations de Landazuri et Seitz évoquées à la fin du paragraphe 3.2 permettent de généraliser ces résultats : les ≪ grandes parties ≫ des groupes finis simples de type de Lie ont de fortes propriétés d’expansion.
Références
[1] R. ANTETOMASO, Autour du théorème de Jordan sur les sous-groupes finis de GLn(C ), RMS 124-3 (2014), 3-8
[2] L. BABAI, V.T. SÒS, Sidon sets in groups and induced subgraphs of Cayley Graphs, Europ. J. Combin. 6 (1985), 101-114
[3] L. BABAI, N. NIKOLOV, L. PYBER, Product Growth and Mixing in Finite Groups, Proceedings of the Nineteenth Annual ACM-SIAM Symposium on Discrete Algorithms, 248-257, ACM, New York, 2008
[4] W. GOWERS, Quasirandom groups, Combin. Probab. Comput. 17 (2008), no.3, 363-387
[5] E. BREUILLARD, A brief introduction to approximate groups, Thin groups and superstrong approximation, MSRI Publications, vol 61, 2013, 23-50
[6] B. GREEN, I.Z. RUSZA, Sum-free sets in abelian groups, Israel J. Math 147 (2005), p. 157-189
[7] K. KEDLAYA, Large product-free subsets of finite groupes, J. Combin. Theory Series A 77 (1997), 339-343
[8] E. KOWALSKI, An Introduction to the Representation Theory of Groups, AMS, 2014
[9] N. NIKOLOV, L.PYBER, Product decomposition of quasirandom groups and a Jordan type theorem, J. Eur. Math. Soc., 13 (2011), 1063-1077
[10] T. TAO, Expansion in Finite Simple Groups of Lie Type, AMS, 2015
[11] T. TAO, V.H. VU, Additive Combinatorics, Cambridge, 2006
[Table des matières]