[Table des matières]
Quel est le maximum de la dimension
d’un sous-espace vectoriel de
 (n, R) dont tout élément non nul
est
inversible ?1
(n, R) dont tout élément non nul
est
inversible ?1
par Richard Antetomaso et Alain Tissier
Comité de rédaction de la RMS
Résumé. tant donné un espace vectoriel euclidien E, on établit une relation entre les sous-espaces vectoriels de
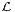 (E) dont tout élément non nul est inversible et les ensembles de champs continus de vecteurs sur la sphère
unité de E. Un théorème dû à J. F. Adams, admis ici, donne une limitation sur le nombre de champs continus
linéairement indépendants. Une construction de certains tels sous-espaces vectoriels, due à J.Radon et
A.Hurwitz, sera développée ici ; elle permet de conclure.
(E) dont tout élément non nul est inversible et les ensembles de champs continus de vecteurs sur la sphère
unité de E. Un théorème dû à J. F. Adams, admis ici, donne une limitation sur le nombre de champs continus
linéairement indépendants. Une construction de certains tels sous-espaces vectoriels, due à J.Radon et
A.Hurwitz, sera développée ici ; elle permet de conclure.
Abstract. Maximal dimension of a subspace of 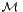 (n,R) whose every element is invertible.
(n,R) whose every element is invertible.
If E is an euclidian vector space, one establishes a relation between the subspaces of 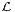 (E) whose every
element is invertible and the sets of continuous vector fields on the unit sphere of E. A theorem due to J. F.
Adams, which is admitted here, gives a limitation on the number of such fields which are linearly independants.
A construction of some such subspaces, due to J.Radon et A.Hurwitz, will be given here ; it will give the
conclusion.
(E) whose every
element is invertible and the sets of continuous vector fields on the unit sphere of E. A theorem due to J. F.
Adams, which is admitted here, gives a limitation on the number of such fields which are linearly independants.
A construction of some such subspaces, due to J.Radon et A.Hurwitz, will be given here ; it will give the
conclusion.
Mots-clés : champs de vecteurs sur la sphère ; théorème d’Adams ; nombres de Radon-Hurwitz ; produit de Kronecker.
La question 499 de la RMS, posée dans la RMS 114 2, était formulée ainsi :
≪Soit E un espace vectoriel réel de dimension n. Pour n = 4, caractériser les sous-espaces
vectoriels 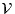 de
de  (E) tels que
(E) tels que 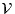 \{0}⊂ GL(E) et dim
\{0}⊂ GL(E) et dim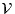 = 4.
= 4.
Pour n quelconque, trouver la dimension maximale d’un espace du type 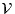 . ≫
. ≫
Dans cet article, nous répondons à la deuxième question. On supposera E muni d’une structure euclidienne, ce qui ne modifie en rien les résultats demandés.
Pour tout espace euclidien E, notons 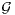 (E) l’ensemble constitué par le groupe linéaire GL(E) et
l’endomorphisme nul.
(E) l’ensemble constitué par le groupe linéaire GL(E) et
l’endomorphisme nul.
Notons γ(n) la plus grande dimension d’un sous-espace vectoriel (en abrégé : s.e.v.) de  (E)
inclus dans
(E)
inclus dans 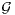 (E), n étant la dimension de E.
(E), n étant la dimension de E.
Le nombre de Radon-Hurwitz est 8r + 2s si n = 24r+sm où m est impair et 0 ≤ s ≤ 3. On le note ρ(n).
1.Champs de vecteurs sur la sphère unité et le théorème d’Adams
Dans un espace euclidien E de dimension n, S étant sa sphère unité, un champ de vecteurs sur S est une application continue f qui envoie tout élément v de S sur un vecteur f(v) tangent en v à S.
Les p champs de vecteurs sur S, f1, f2, . . ., fp, sont dits linéairement indépendants si pour tout v de S, les vecteurs f1(v), f2(v), . . ., fp(v) sont linéairement indépendants.
Le théorème d’Adams s’énonce ainsi :
Théorème 1.Il n’existe pas ρ(n) champs de vecteurs linéairement indépendants sur la sphère unité d’un espace euclidien de dimension n (où ρ(n) est le nombre de Radon-Hurwitz).
Dans [1], J.F. Adams prouve ce théorème en réduisant le problème initial à un problème d’homotopie relatif aux espaces projectifs. Nous n’en dirons pas plus sur cette preuve.
2.Relation
entre
s.e.v.
inclus
dans
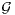 (E)
et
champs
sur
S
(E)
et
champs
sur
S
Soit F un s.e.v. de  (E) inclus dans
(E) inclus dans 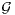 (E), de dimension p. On lui associe p- 1 champs de vecteurs
linéairement indépendants par la méthode suivante.
(E), de dimension p. On lui associe p- 1 champs de vecteurs
linéairement indépendants par la méthode suivante.
Quitte à multiplier les éléments de F par l’inverse de l’un d’eux (cette opération maintient
l’inclusion dans 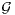 (E) et la dimension), on peut supposer que F contient idE. Considérons, dans F ,
p - 1 éléments g1,g2,…,gp-1 constituant avec idE une base de F . Comme tout élément non nul
de F est de noyau nul, pour tout v de S, les vecteurs v,g1(v),…,gp-1(v) sont indépendants. Notons
fi (v) := gi (v) -
(E) et la dimension), on peut supposer que F contient idE. Considérons, dans F ,
p - 1 éléments g1,g2,…,gp-1 constituant avec idE une base de F . Comme tout élément non nul
de F est de noyau nul, pour tout v de S, les vecteurs v,g1(v),…,gp-1(v) sont indépendants. Notons
fi (v) := gi (v) - 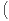 v|gi(v)
v|gi(v)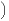 v pour tout i. Chaque fi est un champ de vecteurs sur S et les fi sont
linéairement indépendants au sens précisé plus haut : pour tout v de S les fi(v) sont linéairement
indépendants.
v pour tout i. Chaque fi est un champ de vecteurs sur S et les fi sont
linéairement indépendants au sens précisé plus haut : pour tout v de S les fi(v) sont linéairement
indépendants.
Le théorème 1 permet donc d’affirmer γ(n) ≤ ρ(n).
3.Le théorème de Radon et Hurwitz
On dit d’un système (f1,f2,…,fq) d’éléments de  (E) qu’il est de type (A) lorsque, pour tout i,
f
(E) qu’il est de type (A) lorsque, pour tout i,
f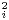 = - id E et fi fj + fjfi = 0 pour tous i,j distincts.
= - id E et fi fj + fjfi = 0 pour tous i,j distincts.
Notons W le s.e.v. engendré par un tel système. Un élément de W s’écrit f = 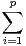 tifi pour certains
réels ti ; il vérifie : f2 = -
tifi pour certains
réels ti ; il vérifie : f2 = -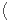
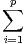 t
t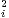
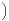 idE. On en déduit que les fi sont linéairement indépendants.
De plus un élément non nul de W n’a aucune valeur propre réelle. Il en résulte que le s.e.v.
W ⊕ R id E , de dimension p + 1 est inclus dans
idE. On en déduit que les fi sont linéairement indépendants.
De plus un élément non nul de W n’a aucune valeur propre réelle. Il en résulte que le s.e.v.
W ⊕ R id E , de dimension p + 1 est inclus dans 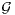 (E).
(E).
Une méthode, due à J.Radon et A.Hurwitz, développée dans le problème [2] et décrite dans la partie suivante, a permis de construire dans tout espace vectoriel réel de dimension n un système de type (A) qui est de taille ρ(n) - 1 où ρ(n) est le nombre de Radon-Hurwitz. Ceci achève la preuve de l’égalité entre γ(n) et ρ(n).
4.Construction d’un système de Radon-Hurwitz
Dans le problème [2], on utilise la structure euclidienne de Rn et la notion d’endomorphisme adjoint. On traitera la question matriciellement de façon similaire, sans recours aux adjoints.
On note 0(n) la matrice nulle d’ordre n et I(n) la matrice unité d’ordre n. Traduisons matriciellement la définition fondamentale.
Définition 1.Dans  (n,R), (A1,A2,…,Ak) est un (A)-système si les relations suivantes sont
vérifiées :
(n,R), (A1,A2,…,Ak) est un (A)-système si les relations suivantes sont
vérifiées :
A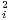 = -I(n) pour tout i ; AiAj + AjAi = 0(n) pour tous i,j distincts.
= -I(n) pour tout i ; AiAj + AjAi = 0(n) pour tous i,j distincts.
Puisque de telles matrices n’existent pas si n est impair, on suppose n pair.
On doit construire pour tout n, dans  (n, R), un (A)-système de ρ(n) - 1 matrices.
(n, R), un (A)-système de ρ(n) - 1 matrices.
On utilise le produit de Kronecker. Pour tous A = (ai,j) de  (n, R) et B de
(n, R) et B de  (m, R) on définit
par blocs :
(m, R) on définit
par blocs :
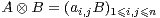
et de même B ⊗ A. L’application (A,B) A⊗B va de
A⊗B va de  (n, R) ×
(n, R) × (m, R) dans
(m, R) dans  (nm, R),
est bilinéaire et vérifie
(nm, R),
est bilinéaire et vérifie
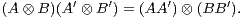
On utilisera beaucoup le lemme 1 dont la preuve est immédiate.
Lemme 1.Soit m et n des entiers strictement positifs. Soit (A1,A2,…,Ak) un (A)-système
de  (n, R ). Alors les systèmes
(n, R ). Alors les systèmes  A1 ⊗ I(m),A2 ⊗ I(m),…,Ak ⊗ I(m)
A1 ⊗ I(m),A2 ⊗ I(m),…,Ak ⊗ I(m) , d’une part, et
, d’une part, et
 I(m)⊗A1,I(m)⊗A2,…,I(m)⊗Ak
I(m)⊗A1,I(m)⊗A2,…,I(m)⊗Ak , d’autre part, sont des (A)-systèmes de
, d’autre part, sont des (A)-systèmes de  (mn,R).
(mn,R).
Comme ρ(mn) = ρ(n) si m est impair, le lemme 1 permet de se limiter au cas où n = 2h pour un certain h de N * . La construction se fait par récurrence, la suite des ρ(2h) vérifiant :
ρ(2) = 2 ; ρ(4) = 4 ; ρ(8) = 8 ; ρ(2h+4) = ρ(2h) + 8.
On part des matrices :
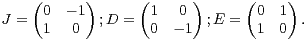
Les relations vérifiées par ces matrices sont :
- J2 = -D2 = -E2 = -I(2) ;
- JD = -DJ = E ; EJ = -JE = D ; ED = -DE = J.
Dans  (2, R ), (J) est un (A)-système de taille 1 ; la construction est faite pour n = 2 puisque
ρ(2) = 2.
(2, R ), (J) est un (A)-système de taille 1 ; la construction est faite pour n = 2 puisque
ρ(2) = 2.
On dira que deux systèmes commutent si chaque élément de l’un commute avec chaque élément de l’autre.
Dans  (4, R ), les matrices I(2), J, D, E permettent, avec le produit de Kronecker, de construire
deux (A)-systèmes de taille 3 qui commutent entre eux. Ce sont :
(4, R ), les matrices I(2), J, D, E permettent, avec le produit de Kronecker, de construire
deux (A)-systèmes de taille 3 qui commutent entre eux. Ce sont :
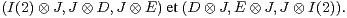
Comme ρ(4) = 4, la construction est faite pour n = 4.
La suite fait intervenir des systèmes d’un autre type.
Définition 2.Dans  (n,R), (B1,B2,…,Bk) est un (B)-système si les relations suivantes
sont vérifiées :
(n,R), (B1,B2,…,Bk) est un (B)-système si les relations suivantes
sont vérifiées :
B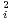 = I(n) pour tout i ; BiBj + BjBi = 0(n) pour tous i,j distincts.
= I(n) pour tout i ; BiBj + BjBi = 0(n) pour tous i,j distincts.
En particulier, dans  (2, R), (D,E) est un (B)-système de taille 2. Deux autres lemmes de preuve
immédiate seront utiles.
(2, R), (D,E) est un (B)-système de taille 2. Deux autres lemmes de preuve
immédiate seront utiles.
Lemme 2.Soit dans  (n,R), un (A)-système (A1,A2,…,Ak) et un (B)-système (B1,B2)
qui commutent. Alors (B1,B2,A1B1B2,…,AkB1B2) est un (B)-système de
(n,R), un (A)-système (A1,A2,…,Ak) et un (B)-système (B1,B2)
qui commutent. Alors (B1,B2,A1B1B2,…,AkB1B2) est un (B)-système de  (n,R).
(n,R).
Lemme 3.Soit dans  (n,R), un (B)-système (B1,B2,…,Bk) et un (A)-système (A1,A2)
qui commutent. Alors (A1,A2,B1A1A2,…,BkA1A2) est un (A)-système de
(n,R), un (B)-système (B1,B2,…,Bk) et un (A)-système (A1,A2)
qui commutent. Alors (A1,A2,B1A1A2,…,BkA1A2) est un (A)-système de  (n,R).
(n,R).
On construit à présent dans  (8, R) un (A)-système d’ordre 6. On utilise pour cela, dans
(8, R) un (A)-système d’ordre 6. On utilise pour cela, dans  (4, R),
deux (A)-systèmes (A1,A2) et (A3,A4) qui commutent. Par exemple :
(4, R),
deux (A)-systèmes (A1,A2) et (A3,A4) qui commutent. Par exemple :
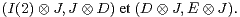
Le (A)-système  A1 ⊗I(2),A2 ⊗I(2)
A1 ⊗I(2),A2 ⊗I(2) , le (B)-système
, le (B)-système  I(4) ⊗D,I(4) ⊗E
I(4) ⊗D,I(4) ⊗E et le (A)-système
et le (A)-système
 A3 ⊗I(2),A4 ⊗I(2)
A3 ⊗I(2),A4 ⊗I(2) sont des systèmes de
sont des systèmes de  (8, R) qui commutent deux à deux. On applique le
lemme 2 aux deux premiers pour construire un (B)-système (B1,B2,B3,B4) qui commute avec
(8, R) qui commutent deux à deux. On applique le
lemme 2 aux deux premiers pour construire un (B)-système (B1,B2,B3,B4) qui commute avec
 A3 ⊗ I(2),A4 ⊗ I(2)
A3 ⊗ I(2),A4 ⊗ I(2) . Avec ces deux systèmes, on applique le lemme 2 pour construire un
(A)-système de taille 6.
. Avec ces deux systèmes, on applique le lemme 2 pour construire un
(A)-système de taille 6.
Dans  (8, R ) nous disposons à présent d’un (A)-système (A1,A2,…,A6) d’ordre 6. Posons
A7 = A1 A2 A3 A4A5A6. On constate que (A1,A2,…,A6,A7) est un (A)-système de taille 7 ;
puisque ρ(8) = 8, la construction est faite pour n = 8.
(8, R ) nous disposons à présent d’un (A)-système (A1,A2,…,A6) d’ordre 6. Posons
A7 = A1 A2 A3 A4A5A6. On constate que (A1,A2,…,A6,A7) est un (A)-système de taille 7 ;
puisque ρ(8) = 8, la construction est faite pour n = 8.
Montrons que dans  (2h, R), l’existence d’un (A)-système de taille k entraîne l’existence dans
(2h, R), l’existence d’un (A)-système de taille k entraîne l’existence dans
 (2h+4 , R ) d’un (A)-système de taille k + 8. Ceci achèvera la construction par récurrence,
puisque ρ(2h+4 ) = ρ(2h) + 8.
(2h+4 , R ) d’un (A)-système de taille k + 8. Ceci achèvera la construction par récurrence,
puisque ρ(2h+4 ) = ρ(2h) + 8.
On applique le lemme 2, au système des Ai ⊗ I(2) et au système 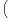 I(2h) ⊗ D,I(2h) ⊗ E
I(2h) ⊗ D,I(2h) ⊗ E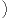 , pour
construire un (B)-système (B1,…,Bk+2) de taille k + 2 dans
, pour
construire un (B)-système (B1,…,Bk+2) de taille k + 2 dans  (2h+1, R). On a vu précédemment
que
(2h+1, R). On a vu précédemment
que  (8, R ) contient deux (A)-systèmes (A1,A2) et (A3,A4) et un (B)-système (Bk+3,Bk+4)
qui commutent deux à deux.
(8, R ) contient deux (A)-systèmes (A1,A2) et (A3,A4) et un (B)-système (Bk+3,Bk+4)
qui commutent deux à deux.
On pose alors Bʹi := Bi ⊗ I(8) pour i = 1,2,…,k + 2, Aʹj := I(2h+1) ⊗ Aj pour j = 1,2,3,4,
Bʹj := I(2h+1 ) ⊗ Bj pour j = k + 3,k + 4. Dans  (2k+4, R) les quatre systèmes
(Bʹ1 , … , Bʹk+2 ), (Aʹ1,Aʹ2), (Aʹ3,Aʹ4), (Bʹk+3,Bʹk+4) commutent deux à deux. On utilise
successivement les lemmes 3, 2, 3 pour construire un (B)-système de taille k + 6 dans
(2k+4, R) les quatre systèmes
(Bʹ1 , … , Bʹk+2 ), (Aʹ1,Aʹ2), (Aʹ3,Aʹ4), (Bʹk+3,Bʹk+4) commutent deux à deux. On utilise
successivement les lemmes 3, 2, 3 pour construire un (B)-système de taille k + 6 dans
 (2h+4 , R ).
(2h+4 , R ).
Références
[1] J.F. Adams, Vector Fields on Spheres, Annals of Mathematics, vol. 75, 1962, p. 603-632
[2] Problème de l’ENS de Lyon 1991, première épreuve, énoncé : RMS 102-1, corrigé : RMS 102-6.
[Table des matières]

