[Table des matières]
Du côté des élèves
de Terminale S
Questions proposées aux élèves de Terminale S
1. Déterminer l’ensemble des couples (a,b)  N × N* tels que 2b - 1 divise 2a + 1.
N × N* tels que 2b - 1 divise 2a + 1.
2. Soient n  N * et P un polynôme à coefficients réels de degré inférieur ou égal à n tel que :
∀k
N * et P un polynôme à coefficients réels de degré inférieur ou égal à n tel que :
∀k 
![[[1,n+1]]](/numeros/RMS127-4/RMS127-41370x.png) , P(k) = 2k. Calculer P(n + 2).
, P(k) = 2k. Calculer P(n + 2).
3. Soit A = 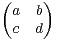
 M2(Z) telle que a + d > 1 et ad - bc = 1. On note (un)n
M2(Z) telle que a + d > 1 et ad - bc = 1. On note (un)n N la suite
d’entiers définies par : u0 = 0, u1 = 1 et ∀n
N la suite
d’entiers définies par : u0 = 0, u1 = 1 et ∀n  N*, un+1 = (a + d)un - un-1.
N*, un+1 = (a + d)un - un-1.
a) ∙ Vérifier que A2 = (a + d)A - I2 où I2 = 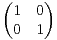 .
.
∙ Montrer que : ∀n  N, ∀k
N, ∀k  N, An = uk+1
N, An = uk+1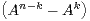 - uk
- uk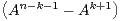 .
.
b) Pour tout n  N, on note dn le plus grand diviseur commun des coefficients de la matrice
An - I2 . Déterminer limn→+∞dn.
N, on note dn le plus grand diviseur commun des coefficients de la matrice
An - I2 . Déterminer limn→+∞dn.
4. Question proposée par Antoine Sirianni.
Dans le plan, M un point et (D) une droite sont donnés. Indiquer une construction de la perpendiculaire à (D) passant par M en utilisant une règle non graduée et en traçant un seul cercle.
Problème : Quelques applications du théorème de Minkowski
L’objet du problème est de proposer en I une démonstration du théorème de Minkowski1 1. Hermann Minkowski 1864-1909. Son théorème est un résultat de géométrie des nombres qu’il a introduit dans ses travaux consacrés à la théorie algébrique des nombres. et d’en présenter quelques conséquences dans les parties suivantes. Le résultat I.1.b) est une conséquence d’un lemme connu sous le nom de lemme de Blichfeldt. La section II présente le théorème de Pick exposé et démontré en II.3. Le problème du verger de la section III a été posé et résolu par G. Polya2 2. George Polya 1887-1985, s’est illustré en théorie des nombres, en combinatoire et par ses travaux sur les marches aléatoires. . L’exercice II de l’épreuve du concours général 2016 présente une variante de cette question. La méthode suivie ici appliquant le théorème de Minkowski est due à Akiva et Isaak Yaglom. La section IV propose quelques conséquences arithmétiques du théorème de Minkowski.
Dans tout le problème, le plan est supposé rapporté au repère orthonormé (O; 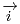 ,
, 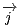 ).
On appelle point intègre tout point du plan dont les deux coordonnées sont des entiers
relatifs.
I. Un cas particulier du théorème de Minkowski
).
On appelle point intègre tout point du plan dont les deux coordonnées sont des entiers
relatifs.
I. Un cas particulier du théorème de Minkowski
Soient Q = 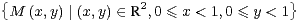 et E une partie bornée du plan d’aire
strictement supérieure à 1. Pour tout z = (x,y)
et E une partie bornée du plan d’aire
strictement supérieure à 1. Pour tout z = (x,y)  Z2, on note Qz l’image de Q par la
translation tz de vecteur
Z2, on note Qz l’image de Q par la
translation tz de vecteur 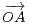 , A étant le point de coordonnées (x,y), Ez l’ensemble E ∩ Qz,
F =
, A étant le point de coordonnées (x,y), Ez l’ensemble E ∩ Qz,
F = 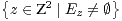 et Δz = t
et Δz = t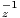 (Ez). T étant un sous-ensemble quarrable du plan, on note
a(T) son aire. Une partie K du plan ou de l’espace est dite convexe si et seulement si :
∀(A, B)
(Ez). T étant un sous-ensemble quarrable du plan, on note
a(T) son aire. Une partie K du plan ou de l’espace est dite convexe si et seulement si :
∀(A, B)  K2 , [AB] ⊂ K.
1. a) Montrer que F est un ensemble fini.
K2 , [AB] ⊂ K.
1. a) Montrer que F est un ensemble fini.
b) Établir que a(E) = 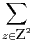 a(Ez) (dans cette somme, il y a un nombre fini de termes non
nuls).
a(Ez) (dans cette somme, il y a un nombre fini de termes non
nuls).
c) En déduire que : 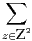 a(Δz) > 1.
a(Δz) > 1.
d) Montrer alors qu’il existe u,v deux éléments distincts de Z2 tels que Δu ∩ Δv≠∅.
e) En déduire qu’il existe deux points distincts de E, M1(x1,y1) et M2(x2,y2) tels
que :
x1 - x2  Z et y1 - y2
Z et y1 - y2  Z.
Z.
2. Soit K une partie du plan convexe, bornée, symétrique par rapport à O, d’aire strictement
supérieure à 4. On note Kʹ l’image de K par l’homothétie de centre O de rapport 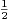 ⋅
⋅
a) Vérifier que Kʹ est convexe, bornée, symétrique par rapport à O et que a(Kʹ) > 1.
b) Montrer qu’il existe (x1,y1)  Z2 et (x2,y2)
Z2 et (x2,y2)  Z2 tels que (x1,y1)≠(x2,y2) et le point de
coordonnées
Z2 tels que (x1,y1)≠(x2,y2) et le point de
coordonnées 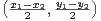 appartient à Kʹ.
appartient à Kʹ.
c) En déduire que K contient au moins un point intègre distinct de O.
d) Montrer que pour garantir le résultat c),
∙ la condition a(K) > 4 est optimale,
∙ on ne peut supprimer l’hypothèse K est convexe.
3. Soient A, B deux points du plan de coordonnées respectives (a,b)  R2 et (c,d)
R2 et (c,d)  R2 tels que
O, A, B ne soient pas alignés. On note C le point tel que
R2 tels que
O, A, B ne soient pas alignés. On note C le point tel que 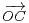 =
= 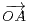 +
+ 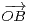 . On appelle réseau de
base (
. On appelle réseau de
base ( 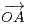 ,
, 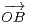 ) l’ensemble L des points M pour lesquels il existe (λ,μ)
) l’ensemble L des points M pour lesquels il existe (λ,μ)  Z2 tel que
Z2 tel que
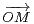 = λ
= λ 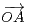 + μ
+ μ 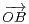 . Le nombre δ =
. Le nombre δ = 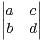 = ad - bc est appelé déterminant de
L.
a) Montrer que l’aire du parallélogramme OACB est égale à
= ad - bc est appelé déterminant de
L.
a) Montrer que l’aire du parallélogramme OACB est égale à 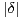 .
.
b) En adaptant la méthode suivie en 2 pour établir 2.c), montrer que si K est une partie du plan
convexe, bornée, symétrique par rapport à O telle que a(K) > 4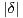 , alors K contient au moins un
point de L distinct de O.
, alors K contient au moins un
point de L distinct de O.
c) Énoncer et démontrer un résultat analogue dans l’espace.
1. Soit T un triangle dont les trois sommets sont intègres.
a) Montrer que a(T) ≥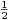 ⋅
⋅
b) On dit que T est primitif si et seulement si les seuls points intègres qu’il contient
sont ses trois sommets. En utilisant I.2.a) montrer que T est primitif si et seulement si
a(T) = 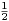 ⋅
⋅
Soit n un entier supérieur ou égal à 3, un polygone simple P de n sommets est déterminé par la
donnée de n points du plan A1,…,An que l’on appelle les sommets de P . On suppose que la ligne
polygonale A1 … AnA1 ne se recoupe pas, autrement dit que la suite de segments ![([AkAk+1 ])](/numeros/RMS127-4/RMS127-41398x.png) 1≤k≤n
où An+1 = A1 vérifie :
1≤k≤n
où An+1 = A1 vérifie :
![{
∀k ∈ [[1,n- 1]], [AkAk+1 ]∩[Ak+1Ak+2] = {Ak+1 },
∀k,ℓ ∈ [[1,n]], ℓ- k ≥ 2 =⇒ [AkAk+1 ]∩[AℓAℓ+1] = ∅.](/numeros/RMS127-4/RMS127-41399x.png)
La ligne polygonale A1…AnA1 que l’on appelle le bord de P partage le plan en deux régions disjointes, l’une non bornée, l’autre bornée et contenant le bord de P appelée intérieur de P et notée int (P). Une diagonale de P est un segment ayant pour extrémités deux sommets non consécutifs de P et inclus dans int(P). Enfin une triangulation de P est la donnée d’une famille finie de triangles (Tj)1≤j≤m (les Tj étant entendus comme l’enveloppe convexe de leurs sommets, c’est-à-dire comme plaques triangulaires) dont la réunion est int(P) et telle que pour toute paire j,k d’indices distincts, Tj ∩ Tk = ∅ ou bien Tj ∩ Tk est réduit à un point qui est alors un sommet commun ou bien Tj ∩ Tk est un segment qui est alors une arête commune. Dans la suite, on appelle polygone simple intègre tout polygone simple dont tous les sommets sont intègres.
2. a) Montrer que tout polygone simple d’au moins quatre sommets possède une diagonale.
b) Montrer que tout polygone simple de n sommets admet une triangulation formée de n - 2 triangles dont les sommets sont des sommets de P .
c) En déduire que tout polygone simple intègre admet une triangulation formée de triangles intègres.
d) Montrer alors que tout polygone simple intègre admet une triangulation formée de triangles intègres primitifs.
L’aire du polygone simple P que l’on note a(P) est l’aire du domaine plan int(P). Un point strictement intérieur à P est un point de int(P) non situé sur le bord de P .
3. Soit P un polygone simple intègre. On note B le nombre de points intègres situés sur le bord de P et I le nombre de points intègres strictement intérieurs à P . Montrer que :
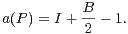
Ind. Remarquer d’abord que le résultat est vrai si P est un triangle intègre primitif. Dans le cas général, considérer une triangulation de P formée de m triangles intègres primitifs et montrer en déterminant de deux façons la somme des angles de tous ces triangles que m = 2I + B - 2.
4. Soit ABC un triangle intègre. Montrer que ABC ne peut être équilatéral.
5. Soient n  N * et Q un carré du plan de côté de longueur n. On note N le nombre de points
intègres appartenant à int(Q).
N * et Q un carré du plan de côté de longueur n. On note N le nombre de points
intègres appartenant à int(Q).
a) Montrer que : N ≤ (n + 1)2.
b) Donner une condition nécessaire et suffisante pour que N = (n + 1)2.
Soient R  N * , ΔR le disque fermé de centre O et de rayon R, ER l’ensemble des points intègres
de ΔR distincts de O. En tout point M de ER, on suppose planté un arbre figuré par le disque fermé
de centre M et de rayon r > 0 ; tous les arbres centrés en un point de ER ont même diamètre 2r et
forment un verger V R. Une ligne de vision est une demi-droite d’origine O dont tous les points sont
visibles depuis O, c’est-à-dire dont la vue n’est obstruée par aucun des arbres formant
V R . On se propose de montrer que si r <
N * , ΔR le disque fermé de centre O et de rayon R, ER l’ensemble des points intègres
de ΔR distincts de O. En tout point M de ER, on suppose planté un arbre figuré par le disque fermé
de centre M et de rayon r > 0 ; tous les arbres centrés en un point de ER ont même diamètre 2r et
forment un verger V R. Une ligne de vision est une demi-droite d’origine O dont tous les points sont
visibles depuis O, c’est-à-dire dont la vue n’est obstruée par aucun des arbres formant
V R . On se propose de montrer que si r < 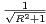 , il existe une ligne de vision pour le
verger V R et si r >
, il existe une ligne de vision pour le
verger V R et si r > 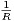 , il n’existe aucune ligne de vision. Dans ce qui suit, M étant
un point du plan et δ désignant une droite du plan, on note d(M,δ) la distance de M à
δ.
, il n’existe aucune ligne de vision. Dans ce qui suit, M étant
un point du plan et δ désignant une droite du plan, on note d(M,δ) la distance de M à
δ.
1. Soit A le point de coordonnées (R,1).
a) Montrer que ER ∩ [OA] = ∅.
b) Montrer que : minM ERd(M,(OA)) =
ERd(M,(OA)) = 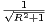 ⋅
⋅
c) En déduire que si r < 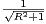 , la demi-droite d’origine O qui contient A est une ligne de
vision.
, la demi-droite d’origine O qui contient A est une ligne de
vision.
2. On suppose que r > 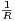 ⋅
⋅
a) Montrer que cette condition impose R ≥ 3 et qu’alors 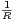 < r ≤
< r ≤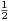 ⋅
⋅
Soit ε > 0 tel que r = 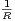 + ε. On raisonne par l’absurde en supposant qu’il existe une ligne de
vision. Soit P le point d’intersection de cette demi-droite avec CR le cercle de centre O et de rayon
R. Soient A et B les deux points de la tangente en P à CR tels que OA = OB =
+ ε. On raisonne par l’absurde en supposant qu’il existe une ligne de
vision. Soit P le point d’intersection de cette demi-droite avec CR le cercle de centre O et de rayon
R. Soient A et B les deux points de la tangente en P à CR tels que OA = OB = 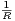 +
+ 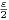 , et Aʹ, Bʹ
les symétriques respectifs de A et B par rapport à O. On note K l’intérieur du rectangle
ABAʹBʹ.
, et Aʹ, Bʹ
les symétriques respectifs de A et B par rapport à O. On note K l’intérieur du rectangle
ABAʹBʹ.
b) Montrer que K contient un point intègre Q tel que 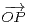 ⋅
⋅ 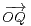 > 0.
c) Montrer que Q
> 0.
c) Montrer que Q  ER.
ER.
d) En déduire que d(Q,(OP)) < r. Relever une contradiction et conclure.
IV. Quelques applications arithmétiques
1. Soit (a1 , a2 , b1,b2)  R4 tel que d = a1b2 - a2b1≠0 ; pour i
R4 tel que d = a1b2 - a2b1≠0 ; pour i 
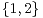 , on note φi : R2-→R,
(x, y)
, on note φi : R2-→R,
(x, y) ai x + bi y.
ai x + bi y.
a) Soit (λ1 , λ2 )  R
R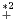 tel que λ1λ2 ≥
tel que λ1λ2 ≥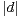 . Montrer en appliquant I.3.b) qu’il existe
(x, y)
. Montrer en appliquant I.3.b) qu’il existe
(x, y)  Z 2 \
Z 2 \ 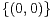 tel que pour tout i
tel que pour tout i 
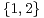 ,
, 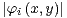 ≤ λi.
≤ λi.
b) Montrer qu’il existe (x,y)  Z2 \
Z2 \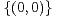 tel que
tel que 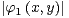 +
+ 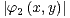 ≤
≤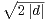 .
.
c) En déduire qu’il existe (x,y)  Z2 \
Z2 \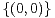 tel que
tel que 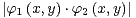 ≤
≤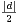 .
.
d) Montrer qu’il existe (x,y)  Z2 \
Z2 \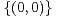 tel que
tel que 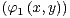 2 +
2 +  2 ≤
2 ≤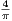
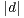 .
.
2. Soit p un nombre premier impair.
a) Montrer que si p est somme de deux carrés d’entiers alors p ≡ 1[4].
Réciproquement, on suppose que p est premier tel que p ≡ 1[4].
b) Montrer qu’il existe a  Z, tel que a2 ≡-1[p].
Z, tel que a2 ≡-1[p].
c) On pose X = pu + av et Y = v où (u,v)  Z2. Montrer qu’il existe (u,v)
Z2. Montrer qu’il existe (u,v)  Z2 \
Z2 \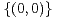 tel
que : X2 + Y 2 ≤
tel
que : X2 + Y 2 ≤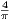 p.
p.
d) En déduire que p est somme de deux carrés d’entiers.
e) Caractériser l’ensemble des nombres entiers naturels non nuls qui sont somme de deux carrés d’entiers.
3. Soit α  R \ Q et Q
R \ Q et Q  N tel que Q ≥ 2.
N tel que Q ≥ 2.
a) Montrer qu’il existe (x,y)  Z2 \
Z2 \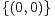 tel que :
tel que : 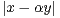 ≤
≤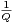 ,
, 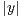 ≤ Q et
x ∧ y = 1.
≤ Q et
x ∧ y = 1.
b) En déduire que pour tout Q ≥ 2, il existe un couple (xQ,yQ)  Z × N* tel que
Z × N* tel que
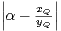 ≤
≤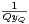 ≤
≤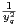 et xQ ∧ yQ = 1.
et xQ ∧ yQ = 1.
c) Montrer alors qu’il existe une infinité33. D’après le théorème de Hurwitz, il existe une infinité de nombre rationnels r = 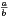 avec (a,b)
avec (a,b) 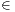 Z ×N*,
a ∧ b = 1 et
Z ×N*,
a ∧ b = 1 et 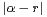 ≤
≤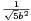 et la constante
et la constante 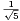 est optimale.
de nombres rationnels r =
est optimale.
de nombres rationnels r = 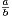 avec (a,b)
avec (a,b)  Z × N*, a ∧ b = 1 et
Z × N*, a ∧ b = 1 et  ≤
≤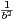 ⋅
⋅
Solutions des questions 1,2 et 3 parues dans la RMS 127-2
1. Soient P un polynôme à coefficients dans Z. On suppose qu’il existe deux entiers relatifs distincts tels que P(a)P(b) = -(a - b)2.
Montrer que P(a) + P(b) = 0.
Solution. P  Z [X] , donc pour tout (a,b)
Z [X] , donc pour tout (a,b)  Z2, a - b∣P(a) - P(b). En effet pour tout k
Z2, a - b∣P(a) - P(b). En effet pour tout k  N*,
ak - bk = (a - b)
N*,
ak - bk = (a - b)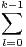 albk-1-l et
albk-1-l et 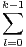 albk-1-l
albk-1-l  Z si a,b sont des entiers relatifs. En particulier, si
a≠ b,
Z si a,b sont des entiers relatifs. En particulier, si
a≠ b, 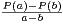
 Z.
Z.
Considérons le polynôme Q(x) = x2 -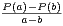 x + 1 : Q est à coefficients entiers. Posons pour
la suite m =
x + 1 : Q est à coefficients entiers. Posons pour
la suite m = 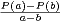 ⋅ Les racines xʹ et xʹʹ de Q sont caractérisées par : xʹ + xʹʹ =
⋅ Les racines xʹ et xʹʹ de Q sont caractérisées par : xʹ + xʹʹ = 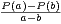 et
xʹxʹʹ = 1 =
et
xʹxʹʹ = 1 = 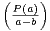 ⋅
⋅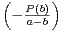 , donc à l’ordre près
, donc à l’ordre près
xʹ = 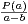 et xʹʹ = -
et xʹʹ = -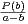 =
= 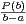 et xʹ,xʹʹ sont des nombres rationnels.
et xʹ,xʹʹ sont des nombres rationnels.
Soit r = 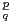 où p
où p  Z, q
Z, q  N* et p ∧ q = 1. Si r est racine de Q alors
N* et p ∧ q = 1. Si r est racine de Q alors
p2 - mpq + q2 = 0 (1).
D’après (1), q∣ p2 . Or p∧q = 1 donc p2 ∧q = 1, par conséquent q = 1. Alors d’après (1), p∣1, donc
p 
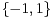 , d’où r
, d’où r 
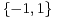 . Donc xʹ = xʹʹ = ±1 puisque xʹxʹʹ = 1.
. Donc xʹ = xʹʹ = ±1 puisque xʹxʹʹ = 1.
Ainsi, 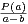 = -
= -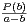 , donc P(a) + P(b) = 0.
, donc P(a) + P(b) = 0.
2. Soit f une application de R+ dans R dérivable, bornée telle que :
∀x  R + , f(x)fʹ(x) ≥ sinx.
R + , f(x)fʹ(x) ≥ sinx.
Montrer que f n’a pas de limite quand x tend vers + ∞.
Solution. Soit A  R+ tel que ∀x
R+ tel que ∀x  R+,
R+, 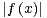 ≤ A. Soit F : R+-→R,
≤ A. Soit F : R+-→R,
x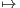 f2 (x) + 2 cosx. On a : ∀x
f2 (x) + 2 cosx. On a : ∀x  R+,
R+, 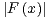 ≤ A2 + 2, ce qui montre que F est bornée. De plus,
F est dérivable et ∀x
≤ A2 + 2, ce qui montre que F est bornée. De plus,
F est dérivable et ∀x  R+, Fʹ(x) = 2
R+, Fʹ(x) = 2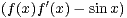 ≥ 0. F est donc croissante ;
étant bornée, F a une limité finie L quand x tend vers + ∞. Supposons par l’absurde
que f ait une limite quand x tend vers + ∞. Puisque f est bornée, cette limite l est
finie. Alors lim x→+∞cosx = limx→+∞
≥ 0. F est donc croissante ;
étant bornée, F a une limité finie L quand x tend vers + ∞. Supposons par l’absurde
que f ait une limite quand x tend vers + ∞. Puisque f est bornée, cette limite l est
finie. Alors lim x→+∞cosx = limx→+∞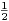
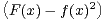 =
= 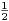
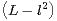 , ce qui est
absurde . En effet, cos
, ce qui est
absurde . En effet, cos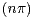 = (-1)n est le terme général d’une suite divergente et
limn→+∞nπ = +∞.
= (-1)n est le terme général d’une suite divergente et
limn→+∞nπ = +∞.
Ainsi f n’a pas de limite quand x tend vers + ∞.
3. Soit E l’ensemble des n  N* pour lesquels il existe n nombres complexes distincts z1,…,zn
tels que : min i≠ j
N* pour lesquels il existe n nombres complexes distincts z1,…,zn
tels que : min i≠ j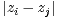 ≥ max1≤k≤n
≥ max1≤k≤n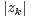 .
.
Montrer que E possède un plus grand élément que l’on précisera.
Solution. Posons r = max1≤i≤n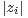 et notons dans le plan complexe Mj le point d’affixe zj ;
1 ≤ j ≤ n. Tous les points Mj se trouvent dans le disque de centre O et de rayon r.
Les zj étant distincts, il y a (au moins) n - 1 de ces nombres distincts de 0. Quitte à
renuméroter les zj, on peut supposer que ces n - 1 nombres sont z2,…,zn et que leurs
arguments principaux sont rangés dans l’ordre croissant. Alors en notant O l’origine et en
convenant que Mn+1 = M2,
et notons dans le plan complexe Mj le point d’affixe zj ;
1 ≤ j ≤ n. Tous les points Mj se trouvent dans le disque de centre O et de rayon r.
Les zj étant distincts, il y a (au moins) n - 1 de ces nombres distincts de 0. Quitte à
renuméroter les zj, on peut supposer que ces n - 1 nombres sont z2,…,zn et que leurs
arguments principaux sont rangés dans l’ordre croissant. Alors en notant O l’origine et en
convenant que Mn+1 = M2, 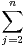
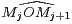 = 2π, . Il existe donc l
= 2π, . Il existe donc l 
![[[2,n]]](/numeros/RMS127-4/RMS127-41478x.png) tel que
tel que
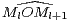 ≤
≤ 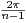 ⋅
⋅
Supposons n ≥ 8 et posons α = 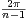 .
.
L’homothétie de centre O et de rapport λ = 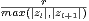 ≥ 1 transforme le triangle OMlMl+1
en le triangle OTU tel que OT = r et OU = x
≥ 1 transforme le triangle OMlMl+1
en le triangle OTU tel que OT = r et OU = x  ]0,r].
]0,r].
Alors 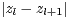 = MlMl+1 ≤ TU et TU2 = f(x) = x2 + r2 - 2rxcosα.
= MlMl+1 ≤ TU et TU2 = f(x) = x2 + r2 - 2rxcosα.
La fonction f ayant un minimum en x0 = r cosα on a :
∀x  ]0, x0 ], f(x) < f(0) = r2 et ∀x
]0, x0 ], f(x) < f(0) = r2 et ∀x  [x0,r],f(x) ≤ f(r) = 2r2(1-cos(α)) =
[x0,r],f(x) ≤ f(r) = 2r2(1-cos(α)) = 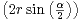 2 ≤
2 ≤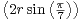 2 < r2
car 0 < sin
2 < r2
car 0 < sin 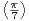 < sin
< sin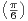 =
= 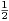 ⋅ Ainsi TU < r donc
⋅ Ainsi TU < r donc 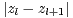 < r, ce qui contredit l’hypothèse.
Par conséquent n ≤ 7.
< r, ce qui contredit l’hypothèse.
Par conséquent n ≤ 7.
Pour n = 7, considérons la configuration formée par 7 points distincts dont un en O et les six autres
formant un hexagone régulier. Il est alors clair que les affixes de ces 7 points forment une famille
répondant à l’hypothèse. Le plus grand élément de E est donc l’entier 7.
[Table des
matières]

