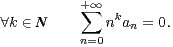[Questions-Reponses]

R897. Posée dans RMS 126-3.

Soit X une variable aléatoire à valeurs dans N ayant un moment à tout ordre. La suite (E(Xk))k∈N détermine-t-elle la loi de X ? (Clément de Seguins Pazzis)

Réponse de Rafik Imekraz et Hervé Queffélec

La réponse est négative. Nous donnons ci-joint deux réponses. On trouvera un éclairage quantitatif de ces résultats dans la rubrique ≪ Articles ≫ de la présente revue à l’aide des théorèmes de Denjoy-Carleman et de Korenbljum (voir le théorème 1, page §).

Les deux solutions que nous donnons ici reposent essentiellement sur le résultat suivant.

Proposition 1.Il existe une suite non nulle (an)n∈N ∈RN qui vérifie

+∑∞ ∀k ∈ N nkan = 0. n=0
(1)

1) Réponse à partir de la proposition 1

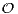On note (an )n∈N comme dans la proposition 1 précédente ainsi que xn = max(an,0) et yn = - min (an , 0). Nous avons donc an = xn - yn et |an| = xn + yn. Remarquons maintenant que la suite (an )n∈N est à décroissance rapide, c’est-à-dire que pour tout k ∈ N on a an = O(n-k ). Il s’ensuit que la série 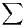∑nk|an| converge pour tout k ∈ N. Il en est de même des deux séries à termes positifs 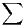∑nkxn et 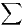∑nkyn et (1) permet même d’affirmer que leurs sommes sont identiques (disons égales à Sk). D’après l’énoncé de la proposition 1, il existe au moins un entier n0 ≥ 1 tel que an0≠0, c’est-à-dire xn0≠yn0. En particulier, on a S0 > 0 et

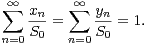∑∞ xn ∞∑ yn S-= S--= 1. n=0 0 n=0 0

Considérons maintenant les deux variables aléatoires X et Y définies par les formules P(X = n) = 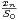xn S0 et P(Y = n) = 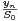yn S0 pour tout n ∈ N. Par construction, les lois de X et Y sont différentes mais l’on a

1 ∑ ∀k ∈ N E[Xk ] = E[Yk] =-- nk |an|. 2S0 n∈N
(2)

2) Preuve de la proposition 1 grâce aux séries de Fourier

Considérons la fonction f : [0,π] → R définie par la formule f(x) = exp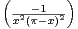( ---1---) x2(π-x)2. Il est bien connu que l’on a

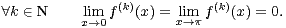(k) (k) ∀k ∈ N xli→m0 f (x) = xli→mπf (x) = 0.

Cela nous permet de prolonger f en une fonction paire, 2π-périodique et de classe C∞ sur R. On a même f(k) (0) = 0 pour tout k ∈ N (notons que cela est trivial si k est impair mais, comme on va le voir immédiatement, seul le cas k pair est pertinent). On peut donc considérer le développement en série de Fourier de f :

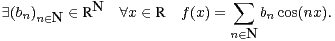N ∑ ∃(bn)n∈N ∈ R ∀x ∈ R f(x) = bncos(nx ). n∈N

La suite (bn )n∈N n’est pas identiquement nulle puisque f ne l’est pas ! En outre, la dérivation terme à terme est licite et l’on a

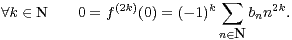∑ ∀k ∈ N 0 = f(2k)(0) = (- 1)k bnn2k. n∈N

Il ne reste plus qu’à poser an2 = bn et am = 0 si m ∈ N n’est pas un carré. La proposition 1 est prouvée.

3) Un exemple explicite et élémentaire

L’exemple qui suit est tiré de [1, page 93]. Fixons un entier q ≥ 2 et considérons la suite (αk)k∈N définie par la formule

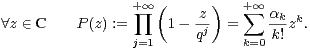( ) +∏∞ -z +∑∞ αk-k ∀z ∈ C P (z) := 1- qj = k! z . j=1 k=0
(3)

Pour donner un sens rigoureux à la définition précédente, deux choix sont possibles :

  • ou bien on peut voir la formule (3) de façon formelle en identifiant les coefficients des puissances de z :
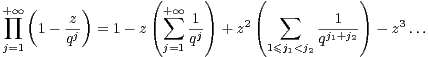
    ( ) ( ) +∏∞( z) ∑+∞ 1 ∑ 1 1- -j = 1 - z( -j) + z2( -j1+j2) - z3... j=1 q j=1 q 1≤j1<j2q

  • ou bien on peut invoquer des produits infinis issus de la théorie des fonctions holomorphes (voir [2, Théorème 15.6]). Le produit infini des monômes 1 -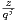zqj est une fonction entière P , et donc est développable en série entière centrée en z = 0. Ce second point de vue permet de voir immédiatement les zéros de la fonction P : ce sont exactement les zéros de ses différents facteurs, soit les nombres z = qj, j = 1,2,…

Cela nous donne une version plus précise de la proposition 1.

Lemme 1.Pour tout n ∈N, on a +∑∞ k=0qknαk k qk! = 0.

Démonstration.Évaluer en z = qn+1 dans (3). __

Lemme 2.Pour tout k ∈N, on a |αk|≤ 1.

Démonstration.L’équation fonctionnelle (1 - z)P(z) = P(qz) vérifiée par le produit infini s’écrit

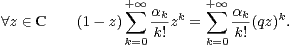+∞ +∞ ∀z ∈ C (1 - z)∑ αkzk = ∑ αk(qz)k. k=0 k! k=0k!

Par identification des coefficients, cela donne pour tout entier k ≥ 1 :

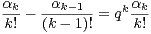αk-- -αk-1--= qkαk- k! (k- 1)! k!

ou encore αk = -k(qk - 1)-1αk-1. Or nous avons qk - 1 ≥ 2k - 1 ≥ k, donc |αk|≤|αk-1|. En remarquant que (3) implique que α0 = 1, on a bien l’inégalité |αk|≤ 1. __

L’exemple le plus connu d’une variable X non déterminée par ses moments ([3, page 227]) est celui d’une variable log-normale (i.e. l’exponentielle d’une variable normale) ; mais cette variable X n’est pas à valeurs entières positives. On peut remédier à cela en considérant une variable ”log-Poisson” (i.e. exponentielle en base entière q ≥ 2 d’une variable de Poisson Z de paramètre q), définie comme suit : X = qZ, autrement dit

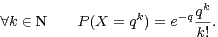qk ∀k ∈ N P (X = qk) = e-qk!.

Nous pouvons maintenant construire une seconde variable aléatoire Y à valeurs entières positives ayant les mêmes moments que X, mais avec une loi différente.

Fixons ε ∈] - 1, 1[ non nul et définissons Y ainsi

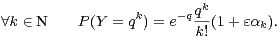k ∀k ∈ N P (Y = qk) = e-qq-(1+ εαk). k!

Comme la suite (αk)k∈N est à valeurs dans [-1,1], la variable aléatoire Y est bien définie. En outre, comme α0 = 1≠0, les lois de X et Y sont différentes. Et le lemme 1 prouve que X et Y ont les mêmes moments. Il nous donne en effet, pour tout n ∈ N :

n ∞∑ -qqk kn ∑∞ -qqk kn n E(Y ) = e k!(1+ εαk)q = e k!q = E(X ). k=0 k=0

Bibliographie

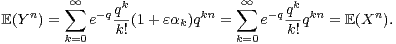
[1] J. Stoyanov, Counterexamples in Probability, John Wiley and Sons, 1987.

[2] W.Rudin, Analyse Réelle et Complexe, chapitre 19, Troisième édition, Dunod, 1998.

[3] W.Feller, An Introduction to Probability Theory and Its Applications, Volume 2, John Wiley and Sons, 2003.
[Questions-Reponses]


[ < ]