[Questions-Reponses]
R848. Posé dans RMS 125-1. Cette question est une reprise de Q585 (RMS 117-3).
Une partition (A, B,C) de [0,1] est dite adéquate si (A+B)∩C = (B +C)∩A = (C +A)∩B = ∅. Existe-t-il une partition adéquate constituée de trois ensembles mesurables et non négligeables ? (Johan Yebbou)
Réponse de Charles Madeline Dérou
On va répondre négativement à la question posée.
Dans la suite on note λ la mesure de Lebesgue sur R.
Pour toute partie mesurable A de R et tout x réel, on dit que x est un point de densité de A si
![λ(A∩[x-h,x+h])
2h](/numeros/RMS127-4/RMS127-41316x.png) tend vers 1 quand h tend vers 0+.
tend vers 1 quand h tend vers 0+.
Le théorème de densité de Lebesgue (dont on trouvera dans [1] un énoncé un peu plus général et une preuve) s’écrit :
Théorème 1.Pour toute partie mesurable A de R, presque tout point x de A est un point de densité de A.
On prouve ensuite une version modifiée du théorème de Steinhaus :
Proposition 1.Si A et B sont deux parties mesurables de R telles que tout point de A est point de densité de A et tout point de B est point de densité de B, alors A + B est ouvert dans R .
Démonstration.Soient A et B deux telles parties ne comportant que des points de densité,
a  A, b
A, b  B. Il existe h > 0 tel que
B. Il existe h > 0 tel que
![λ(A∩[a-h,a+h])
2h](/numeros/RMS127-4/RMS127-41317x.png) ≥
≥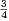 et
et ![λ(B∩[b--h,b+h])-
2h](/numeros/RMS127-4/RMS127-41319x.png) ≥
≥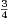 .
.
Notons Aʹ = A ∩ [a - h,a + h] et Bʹ = B ∩ [b - h,b + h] ; on a λ(Aʹ) ≥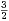 h et λ(Bʹ) ≥
h et λ(Bʹ) ≥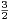 h.
h.
Notons V = ![[a-54h,a + 54h]](/numeros/RMS127-4/RMS127-41323x.png) . Soit ε
. Soit ε 
![]- h4, h4[](/numeros/RMS127-4/RMS127-41324x.png) . Soit bʹ
. Soit bʹ Bʹ ; comme |bʹ- b|≤ h, par
inégalité triangulaire, il vient : |(a + b + ε-bʹ) -a|≤|b-bʹ| + ε < h +
Bʹ ; comme |bʹ- b|≤ h, par
inégalité triangulaire, il vient : |(a + b + ε-bʹ) -a|≤|b-bʹ| + ε < h + 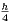 . Ainsi a + b + ε-bʹ
est un point de V , et donc (a + b + ε) - Bʹ est incluse dans V .
. Ainsi a + b + ε-bʹ
est un point de V , et donc (a + b + ε) - Bʹ est incluse dans V .
La partie Aʹ est aussi incluse dans V . Or λ(Aʹ) + λ(a + b + ε-Bʹ) = λ(Aʹ) + λ(Bʹ) ≥ 3h, mais
λ(V ) = 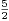 h < 3h, donc Aʹ et (a + b + ε) - Bʹ ne sont pas disjointes.
h < 3h, donc Aʹ et (a + b + ε) - Bʹ ne sont pas disjointes.
Ainsi, pour tout ε 
![]](/numeros/RMS127-4/RMS127-41327x.png) -
-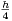 ,
,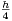
 , a + b + ε
, a + b + ε  Aʹ + Bʹ⊂ A + B ; donc A + B contient un voisinage
de a + b dans R . Finalement A + B est bien ouvert. __
Aʹ + Bʹ⊂ A + B ; donc A + B contient un voisinage
de a + b dans R . Finalement A + B est bien ouvert. __
tant donné E ⊂ R mesurable, on dit que E est voisin de 0 lorsque pour tout δ  ]0,1],
λ(E∩]0, δ]) > 0.
]0,1],
λ(E∩]0, δ]) > 0.
On note que si E est voisin de 0, alors 0 est point d’accumulation de E.
Lemme 1.tant donné (A,B,C), une partition adéquate de [0,1] constituée d’ensembles mesurables et non négligeables, au moins deux des trois ensembles A, B, C sont voisins de 0.
Démonstration.Par l’absurde, supposons avoir une telle partition (A,B,C), où ni B ni
C n’est voisin de 0. Il existe alors (δ1,δ2)  ]0,1]2 tel que B∩]0,δ1] et C∩]0,δ2] sont
négligeables. En prenant δ := min(δ1,δ2), on a λ(A∩]0,δ]) = δ.
]0,1]2 tel que B∩]0,δ1] et C∩]0,δ2] sont
négligeables. En prenant δ := min(δ1,δ2), on a λ(A∩]0,δ]) = δ.
L’application t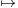 λ(A∩]0,t]) est continue ; on peut donc poser
λ(A∩]0,t]) est continue ; on peut donc poser
![α := max {t ∈ [δ,1];λ(A∩]0,t]) = t}.](/numeros/RMS127-4/RMS127-41332x.png)
Comme C n’est pas négligeable, α≠1, donc 0 < α < 1.
Pour t  ]α, 1], λ(A∩]0,t]) < t, donc λ(A∩]α,t]) < (t - α) et (B ∪ C)∩]α,t] n’est pas
négligeable. En particulier, α est point d’accumulation de (B ∪ C) ∩ [α,1]. Par symétrie, on
peut supposer que α est un point d’accumulation de B ∩ [α,1].
]α, 1], λ(A∩]0,t]) < t, donc λ(A∩]α,t]) < (t - α) et (B ∪ C)∩]α,t] n’est pas
négligeable. En particulier, α est point d’accumulation de (B ∪ C) ∩ [α,1]. Par symétrie, on
peut supposer que α est un point d’accumulation de B ∩ [α,1].
On pose β := max{t  [α,1] : λ(C∩]0,t]) = 0} (cet ensemble contient α). Comme C n’est pas
négligeable, α ≤ β < 1. On distingue deux cas :
[α,1] : λ(C∩]0,t]) = 0} (cet ensemble contient α). Comme C n’est pas
négligeable, α ≤ β < 1. On distingue deux cas :
- : λ
 ]β - α,β]\A
]β - α,β]\A = 0.
= 0.
Il existe une suite (bn) de points de B ∩ [α,1] telle que (bn) → α.
Or : ∀n,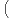 bn + (]β - α,β] ∩ A)
bn + (]β - α,β] ∩ A)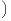 ∩ C = ∅. Par passage à la limite, on montre
facilement :
∩ C = ∅. Par passage à la limite, on montre
facilement : 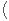 α+(]β-α,β]∩A)
α+(]β-α,β]∩A)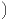 ∩C = ∅. Mais α+(]β-α,β]∩A) est inclus dans
]β, β+α] et, par hypothèse, λ
∩C = ∅. Mais α+(]β-α,β]∩A) est inclus dans
]β, β+α] et, par hypothèse, λ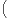 α+(]β-α,β]∩A)
α+(]β-α,β]∩A)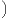 = α. Donc λ(C∩]β,β+α]) = 0,
d’où λ(C∩]0,β + α]) = 0. Alors par définition du maximum, β ≥ β + α ; c’est
absurde puisque α > 0.
= α. Donc λ(C∩]β,β+α]) = 0,
d’où λ(C∩]0,β + α]) = 0. Alors par définition du maximum, β ≥ β + α ; c’est
absurde puisque α > 0.
- λ
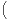 ]β - α,β]\A
]β - α,β]\A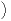 > 0.
> 0.
Alors λ(]β - α,β] ∩ B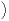 > 0, donc il existe b
> 0, donc il existe b  ]β - α,β] ∩ B ; soit ε
]β - α,β] ∩ B ; soit ε  ]0,α] tel que
b = β - α + ε.
]0,α] tel que
b = β - α + ε.
Alors λ(C∩]β,β + ε]) > 0, donc λ(-b + (C∩]β,β + ε]) > 0. Or : - b + (C∩]β, β + ε]) ⊂]α-ε,α] ⊂]0,α] et λ(A∩]0,α]) = α. Donc les ensembles A∩]0,α] et -b+(C∩]β,β+ε]) ne sont pas disjoints, d’où (b+A)∩C≠∅ puis (B+A)∩C≠∅ : absurde car la partition est adéquate.
Dans les deux cas, on obtient une contradiction, donc par symétrie on conclut qu’au plus un des trois ensembles A, B, C n’est pas voisin de 0. __
Lemme 2.Si (A,B,C) est une partition adéquate telle que 0 est point d’accumulation de A et B, alors C est d’intérieur vide.
Démonstration.Par l’absurde, supposons qu’il existe c < d dans [0,1] tels que ]c,d[⊂ C.
On pose γ := inf{t  [0,c] : ]t,d[⊂ C} : on a ]γ,d[⊂ C. Par hypothèse, 0 est point
d’accumulation de A et B, donc on peut choisir a
[0,c] : ]t,d[⊂ C} : on a ]γ,d[⊂ C. Par hypothèse, 0 est point
d’accumulation de A et B, donc on peut choisir a  A∩]0,d - γ[ et b
A∩]0,d - γ[ et b  B∩]0,d - γ[. On
pose t0 := min (a,b) : alors t0
B∩]0,d - γ[. On
pose t0 := min (a,b) : alors t0  ]0,d[, et t0
]0,d[, et t0  A ∪ B d’où t0
A ∪ B d’où t0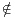 C, donc t0
C, donc t0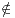 ]γ,d[, et ainsi
t0
]γ,d[, et ainsi
t0  ]0, γ].
]0, γ].
Ainsi γ-t0  [0, γ[, et il existe x
[0, γ[, et il existe x  ]γ-t0,d[ tel que x
]γ-t0,d[ tel que x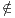 C. Alors x
C. Alors x  ]γ-t0,γ], et x
]γ-t0,γ], et x  A∪B
car la partition est adéquate. Or t0 ≤ a,b < d - γ, d’où x + a,x + b
A∪B
car la partition est adéquate. Or t0 ≤ a,b < d - γ, d’où x + a,x + b  ]γ,d[⊂ C. Mais si
x
]γ,d[⊂ C. Mais si
x  A alors x+b
A alors x+b  A+B et x+b
A+B et x+b  C : absurde, et si x
C : absurde, et si x  B, alors x+a
B, alors x+a  (B +A)∩C :
absurde également. Ainsi C est d’intérieur vide. __
(B +A)∩C :
absurde également. Ainsi C est d’intérieur vide. __
On combine alors les résultats précédents pour conclure :
Proposition 2.Il n’existe pas de partition adéquate de [0,1] constituée d’ensembles mesurables non négligeables.
Démonstration.Par l’absurde on suppose disposer d’une telle partition (A,B,C). D’après
le lemme 1, deux ensembles (au moins) parmi A, B, C sont voisins de 0. Par symétrie, on
suppose que ce sont A et B. Comme φ : t  [0,1]
[0,1] λ(C ∩ [0,t]) est continue, φ(1) est
strictement positif et il existe δ
λ(C ∩ [0,t]) est continue, φ(1) est
strictement positif et il existe δ  ]0,1[ tel que λ(C ∩ [0,1 - δ]) > 0.
]0,1[ tel que λ(C ∩ [0,1 - δ]) > 0.
On considère Aʹ (resp. Bʹ, Cʹ), l’ensemble des points de A ∩ [0,δ] (resp. B ∩ [0,δ], C ∩ [0, 1 - δ]) qui sont des points de densité de A ∩ [0,δ] (resp. B ∩ [0,δ], C ∩ [0,1 - δ]). D’après le théorème 1, Aʹ diffère de A ∩ [0,δ] d’un ensemble négligeable. On en déduit :
- Aʹ est mesurable, et comme un point de densité de A∩ [0,δ] est un point de densité de Aʹ, Aʹ ne contient que des points de densité de Aʹ ;
- Pour δʹ
 ]0,δ], λ(Aʹ∩]0,δʹ]) = λ(A ∩ [0,δ]∩]0,δʹ]) = λ(A∩]0,δʹ]) > 0 car A est
voisin de 0, et donc 0 est un point d’accumulation de Aʹ.
]0,δ], λ(Aʹ∩]0,δʹ]) = λ(A ∩ [0,δ]∩]0,δʹ]) = λ(A∩]0,δʹ]) > 0 car A est
voisin de 0, et donc 0 est un point d’accumulation de Aʹ.
Il en va de même pour Bʹ. Le premier point s’applique aussi à Cʹ : Cʹ diffère de C ∩ [0,1 -δ] (non négligeable) d’un ensemble négligeable, donc :
- Cʹ est non négligeable, donc non vide, et ne contient que des points de densité de Cʹ ;
- 0 est point d’accumulation de A et B (car ces derniers sont voisins de 0), et ainsi
d’après le lemme 2, C est d’intérieur vide.
La partition étant adéquate, (Aʹ + Cʹ⊂ A + C) implique ((Aʹ + Cʹ) ∩ B = ∅).
Or Aʹ ⊂ [0, δ] et Cʹ⊂ [0,1 - δ], donc Aʹ + Cʹ⊂ [0,1] et ainsi Aʹ + Cʹ⊂ A ∪ C.
De même Bʹ + Cʹ⊂ B ∪C, donc (Aʹ + Cʹ) ∩ (Bʹ + Cʹ) ⊂ (A∪C) ∩ (B ∪C) = C car A, B, C sont disjoints.
Or C est d’intérieur vide, mais d’après la proposition 1, Aʹ + Cʹ et Bʹ + Cʹ sont ouverts, donc (Aʹ + Cʹ) ∩ (Bʹ + Cʹ) est un ouvert d’intérieur vide, et (Aʹ + Cʹ) ∩ (Bʹ + Cʹ) = ∅. On en déduit que (Aʹ - Bʹ) ∩ (Cʹ- Cʹ) est vide.
Or 0 est point d’accumulation de Aʹ et Bʹ, donc 0 = 0 - 0 est point d’accumulation de Aʹ- Bʹ. Et d’après la proposition 1, Cʹ- Cʹ est ouvert et contient 0 (car Cʹ non vide), donc (Aʹ - Bʹ) ∩ (Cʹ - Cʹ) n’est pas vide : c’est absurde. Il n’existe donc pas de partition adéquate constituée de trois ensembles mesurables non négligeables. __
[1] C-A. Faure, A Short Proof of Lebesgue’s Density Theorem, The American Mathematical Monthly, Vol. 109, No. 2 (Février 2002), pp. 194-196
[Questions-Reponses]

