[Questions-Reponses]
R599. Posé dans RMS 118-1.
Existe-t-il un corps infini K tel que pour tout entier N ≥ 2, il existe un élément de K qui ne peut pas s’écrire comme somme de puissances N-ièmes d’éléments de K* ? (G. Dospinescu)
Réponse d’Hervé Pépin
Pour tout corps K et tout N de N*, on note SN(K) l’ensemble des sommes de puissances Ne
d’éléments de K*.
On montrera que pour tout corps K, fini ou infini, il existe des entiers N ≥ 2 tels que SN(K) = K et les propositions 1 et 2 donnent les N en question.
La réponse à la question est donc NON, que le corps K soit fini ou infini.
Proposition 1.Soit K un corps infini. L’égalité SN(K) = K est vraie si et seulement si on est dans l’un des trois cas suivants.
- K est de caractéristique nulle et - 1 est une somme de puissances Ne.
- K est de caractéristique non nulle p et N n’est pas multiple de p.
- K est de caractéristique non nulle p et le morphisme de Frobenius de K, ( x
xp) est
surjectif ( c’est-à-dire que K est parfait), et N est multiple de p.
Proposition 2.On note, pour tout entier p premier et tout entier k ≥ 1, Fpk le corps de
cardinal pk . L’égalité SN(Fpk) = Fpk est vraie si et seulement si N n’est multiple d’aucun
des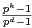 
avec d diviseur strict de k.
La preuve de ces propositions repose sur un résultat préliminaire :
Lemme 1.Soit K un corps quelconque ; SN(K) est un sous-corps de K si et seulement s’il contient - 1.
Démonstration.Il est clair que SN(K) est stable pour la somme et le produit. Pour tout élément x non nul de SN(K), 1⁄x est dans SN(K). En effet 1⁄x = (1⁄x)NxN-1 est un produit d’éléments de SN(K).
Pour être un sous-corps de K, la seule propriété éventuellement manquante de SN(K) est
sa stabilité par x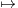
- x, ce qui revient à : - 1 
SN(K). __
Preuve de la proposition 2
D’après le lemme 1, puisque - 1 s’écrit (p - 1)1N, SN(Fpk) est un sous-corps de Fpk. C’est le
corps à pd éléments où d est le plus petit diviseur de k tel que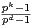 
divise N ; ceci
découle du fait que le groupe multiplicatif de Fpk est cyclique et que les sous-corps de Fpk
sont les corps F pd où d est un diviseur de k. La proposition 2 en résulte immédiatement.
□
Un autre résultat concerne les corps infinis.
Démonstration.L’ensemble KN des puissances Ne d’éléments non nuls de K est un sous-groupe de K* qui est isomorphe au quotient de K* par le groupe des racines Ne de 1 et il est donc infini ; a fortiori SN(K) est infini.
Choisissons dans SN(K), N + 1 éléments distincts a1,a2,…,aN+1.
Pour tout x de K, le vecteur-ligne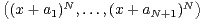 
s’écrit 
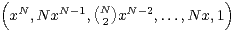V où V est la matrice de Vandermonde de
a1 , a2 , ..., an+1 . La matrice V est inversible dans 
(N,SN(K)) et ceci montre que Nx est
dans SN (K). __
Preuve de la proposition 1
On déduit du lemme 2 que SN(K) = K dans le cas (1) et dans le cas (2) (car - 1 est alors dans SN (K)).
C’est vrai aussi dans le cas (3) ; en effet, en écrivant N = Mpl avec M non multiple de p, on remarque qu’alors SN(K) est l’image de SM(K) par le le itéré du morphisme de Frobenius (donc SN (K) = Kpl ∪{0}) et SN(K) = K si (et seulement si) le morphisme de Frobenius est surjectif.
Réciproquement SN(K) est distinct de K si (et seulement si !) on est dans l’un des deux cas suivants :
1) -1 n’est pas une somme de puissances Ne ( ce qui impose que K est de caractéristique nulle et N est pair).
2) K n’est pas parfait (ce qui impose que la caractéristique de K n’est pas nulle) et N est multiple
de la caractéristique de K. □
Ainsi dans le cas infini, SN(K) = K pour tout N si et seulement si K est de caractéristique nulle et - 1 est une somme de puissances Ne pour tout entier N pair strictement positif ou bien de caractéristique non nulle et parfait.
Par exemple , si K = Fp(X) alors Sp(K) = Fp(Xp).
Les corps finis K tels que SN(K) = K pour tout N sont les Fp.
Omar Sonebi a fourni une solution partielle basée sur les identités :
- (x + 1)3 + (x - 1)3 + (-x)3 + (-x)3 = 6x, si la caractéristique de K diffère de 2 et 3.
- x = x2 + 12 + (x + 1)2 + (x + 1)2 si la caractéristique de K est 3.
[Questions-Reponses]