[Table des matières]

L’irrationalité de π2

par Laurent T’Joen

Lycée Blaise Pascal, Orsay

Résumé. On propose une preuve de l’irrationalité de π2 utilisant des arguments de Desbrow [1] et conforme au programme des classes préparatoires MP.

Abstract. Irrationality of π2

We give a proof of the irrationality of π2 using Desbrow’s arguments [1] and compliant with the MP programme.

Mots-clés : irrationalité, rationnels de Gauss, série entière.

1.Introduction

La première preuve de l’irrationalité de π, on la doit à Lambert qui, en 1761, montre en utilisant les fractions continues que tan(α) n’est pas un rationnel quand α ∈ Q*. On peut noter la preuve très élégante de Niven (1947) qui ne requiert que des calculs élémentaires. Le fait que π2 soit irrationnel a été montré par A.M. Legendre en 1794. Ces résultats ont donné lieu à plusieurs extensions par de nombreux auteurs. En 1873, C. Hermite a démontré la transcendance de e et, en 1882, F. Lindemann a démontré celle de π.

L’objet de cette note est d’établir un résultat dû à Desbrow (1990), qui généralise en outre les résultats indépendants de K. Inkeri (1960) et de T. Estermann (1966) qui montrent que α tanα est irrationnel pour α2 ∈ Q*. On appelle rationnel de Gauss un complexe dont partie réelle et imaginaire sont rationnelles, et on note Q[i] leur ensemble. De même, un entier de Gauss est un complexe dont partie réelle et imaginaire sont des entiers relatifs.

Théorème 1 (Desbrow (1990)).
Il n’existe pas de nombre complexe α non nul tel chα ⁄= 0 et tel que α2 et αth(α) soient des rationnels de Gauss.

Corollaire 1.

(i)
π2 est irrationnel.
(ii)
Si α≠ 0 est un rationnel de Gauss tel chα ⁄= 0, alors th(α) (et donc exp(α)) n’est pas un rationnel de Gauss.

Le point (i) découle directement du théorème avec le choix α = iπ et le point (ii) (dû à B. Novák (1975)) est immédiat en observant que Q[i] est un sous-corps de C.

2.Démonstration du théorème de Desbrow

Pour z ∈ C et α ∈ C*, on pose

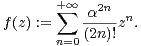+∑ ∞ α2n n f(z) := (2n-)!z . n=0
(1)

Pour z ∈ C , le théorème de Fubini donne

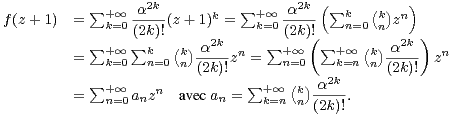2k 2k ( ( ) ) f(z+1) = ∑+k∞=0-α---(z + 1)k = ∑+k∞=0-α--- ∑kn=0 kn zn (2k)! 2k (2k)(! 2k) = ∑+k∞=0∑kn=0(kn)-α---zn = ∑+n∞=0 ∑+k∞=n(kn)-α--- zn (2k)! 2k (2k)! = ∑+ ∞ anzn avecan = ∑+ ∞ (k)-α--. n=0 k=n n (2k)!
(2)

En remarquant que f est une solution sur R de l’équation différentielle

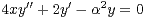4xyʹʹ + 2yʹ - α2y = 0
(3)

et en utilisant le fait que f(x + 1) = 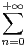+∑∞ n=0anxn pour x ∈ R, on obtient

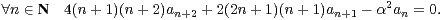∀n∈N 4(n + 1)(n + 2)an+2 + 2(2n + 1)(n + 1)an+1 - α2an = 0.
(4)

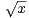De plus, pour tout x ∈ R+, f(x) = ch(α√-- x) et comme, pour tout n ∈ N, f(n) (1) = n!an, on obtient

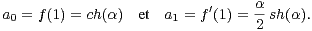a0 = f(1) = ch(α) et a1 = fʹ(1) = α-sh(α). 2
(5)

Par convergence normale, en utilisant (2), on trouve pour ρ > 0

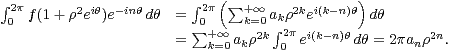
∫2π ∫2π( ∑+ ∞ ) 0f(1+ ρ2eiθ)e- inθdθ = 0 k=0 akρ2kei(k-n)θ dθ = ∑+k∞=0akρ2k∫2π ei(k- n)θdθ = 2πanρ2n. 0

Il apparaît donc que, pour tout n ∈ N,

∫ 2π an = --1-- f(1+ ρ2eiθ)e-inθdθ. 2πρ2n 0
(6)

La définition de f (voir (1)) fournit la majoration

+∑∞ |α|2n • ------ ∀θ∈[0,2π] |f(1+ ρ2eiθ)| ≤ -----(1+ ρ2)n = ch(|α| 1+ ρ2), n=0(2n)!
qui entraîne à son tour que, pour tout n ∈ N,
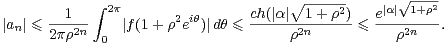√ ---- 1 ∫ 2π ch(|α|•1--+-ρ2) e|α| 1+ ρ2 |an|≤2πρ2n |f(1+ ρ2eiθ)|dθ ≤ ----ρ2n------≤ ---ρ2n--. 0
(7)

Comme an est indépendant de ρ, en choisissant ρ = n, l’inégalité (7) donne

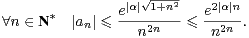√---2 ∀n ∈ N * |a | ≤ e|α|1+n ≤ e2|α|n. n n2n n2n
(8)

Dorénavant, on suppose que α2 et αth(α) sont des rationnels de Gauss.
Alors a0 = ch (α)≠0 et, en multipliant par les dénominateurs, on voit qu’il existe K ∈ N* tel que Kα2 et Kα th (α) soient des entiers de Gauss.

On pose

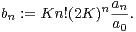a bn := Kn!(2K )n-n. a0
(9)

Compte-tenu de (4) et (5), on obtient

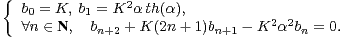{ 2 b0 = K, b1 = K αth(α), 2 2 ∀n ∈ N, bn+2 + K(2n +1)bn+1 - K α bn = 0.
(10)

Une récurrence immédiate montre que bn est un entier de Gauss. Par suite, on trouve par récurrence

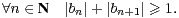∀n ∈ N |bn|+ |bn+1| ≥ 1.
(11)

En effet, si bn+1 ≠ 0, alors |bn+1|≥ 1 et donc |bn+1| + |bn+2|≥ 1. Sinon, bn+1 = 0 et donc |bn+2 | = K2 |α2 bn|≠0, et donc |bn+1| + |bn+2|≥ 1.

Or, en utilisant (9) et l’inégalité (8), on constate que

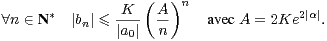
( ) * -K- A- n 2|α| ∀n ∈ N |bn| ≤ |a0| n avec A = 2Ke .
Il en résulte que la suite (bn) tend vers 0 ce qui est absurde compte-tenu de (11).

Références

[1]   D. Desbrow, On the irrationality of π2, Amer. Math. Monthly, 97, pp. 903-906, (1990).

[2]   T. Estermann, A theorem implying the irrationality of π2, J. London Math. Soc., 41, pp. 415-416 (1966).

[3]   K. Inkeri, The irrationality of π2, Nordish Mat. Tidskr., 8, pp. 11-16 (1960).

[4]   I. Niven, A simple proof that π is irrational, Bull. Amer. Math. Soc., 53, pp. 509 (1947).

[5]   B. Novák, A remark to a paper of J.F. Koksma, Nieuw. Arch. Wisk., 23, pp. 195-197 (1975).

Ω
[Table des matières]

[ < ]