 N *. On définit la matrice aléatoire Mn = (Xi,j)1≤i,j,≤n), où les Xi,j sont des
variables de Rademacher indépendantes, P(Xi,j = 1) = P(Xi,j = -1) = 1⁄2.
N *. On définit la matrice aléatoire Mn = (Xi,j)1≤i,j,≤n), où les Xi,j sont des
variables de Rademacher indépendantes, P(Xi,j = 1) = P(Xi,j = -1) = 1⁄2.
a) Calculer E(det(Mn)) et V (det(Mn)).
b) Que dire des lois de det(Mn) et - det(Mn) ?
c) Soit A dans  n(R) ; on pose Y = t A A. Montrer : detY ≤
n(R) ; on pose Y = t A A. Montrer : detY ≤ Y i,i.
Y i,i.
d) Montrer qu’il existe a  ]0,1[ tel que, quand n → +∞, P(|detMn| = nn⁄2) =
]0,1[ tel que, quand n → +∞, P(|detMn| = nn⁄2) =  (an).
(an).
e) Soit ε > 0. Que dire de P(|detMn|≥ nn⁄2-ε) ?
Solution de Arnaud Bégyn
a) ⊳ Par linéarité de l’espérance et indépendance des variables Xi,j,
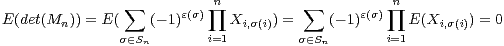
⊳ Toujours par linéarité de l’espérance,
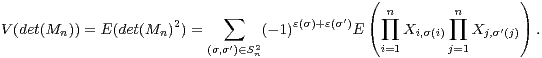
Si σ et σʹ désignent des permutations distinctes, on peut supposer sans perte de généralité que
σ(1)≠ σʹ(1). Alors, comme la variable X1,σ(1) est indépendante de 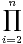 Xi,σ(i)
Xi,σ(i)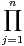 Xj,σʹ(j), on
observe
Xj,σʹ(j), on
observe
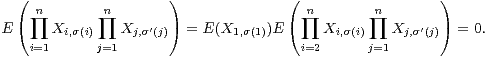
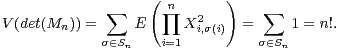
b) Les variables X1,j et - X1,j sont de même loi. Par conséquent, les lois jointes des familles (Xi,j )i,j et ((-1)δi,1Xi,j)i,j sont identiques car les variables sont mutuellement indépendantes dans les deux cas. Ainsi, les variables det(Mn) et - det(Mn) associées au déterminant de chacune de ces familles sont de même loi.
c) Si la matrice A n’est pas inversible, alors det(Y ) = 0 et l’inégalité est évidente car les
coefficients Y i,i sont positifs comme sommes de carrés. Sinon, notons 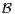 la base canonique de
la base canonique de
 n (R ) puis appliquons le procédé d’orthonormalisation de Gram-Schmidt aux vecteurs colonnes
A1 , … , An de A afin d’obtenir une nouvelle base orthonormée
n (R ) puis appliquons le procédé d’orthonormalisation de Gram-Schmidt aux vecteurs colonnes
A1 , … , An de A afin d’obtenir une nouvelle base orthonormée 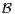 ʹ = (X1,…,Xn) de
ʹ = (X1,…,Xn) de  n(R).
Alors
n(R).
Alors
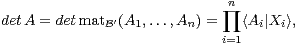
et donc
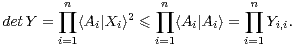
On remarque qu’il y a égalité si, et seulement si, l’une des colonnes de A est nulle ou si les colonnes forment une famille orthogonale libre.
d) Remarquons tout d’abord que
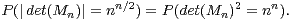
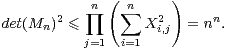
![[ n ] [ n ]
[det(M)2= nn] = ⋂ ∑ M M = 0 ⊂ ⋂ ∑ M M = 0 .
n i<j k=1 k,i k,j ipair k=1 k,i k,i+1](/numeros/RMS127-4/RMS127-41285x.png)
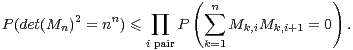
 suit la loi de Bernoulli
suit la loi de Bernoulli 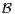 (1⁄2) puis, par indépendance,
(1⁄2) puis, par indépendance,
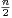 +
+ 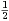
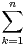 Mk,iMk,i+1 suit une loi binomiale
Mk,iMk,i+1 suit une loi binomiale 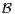 (n,1⁄2).
(n,1⁄2).
⊳ Si n est impair, P(|det(Mn)| = nn⁄2) = 0.
⊳ Si n est pair,
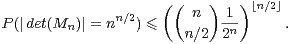
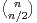
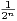 = limn→+∞
= limn→+∞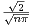 = 0.
= 0.
Pour tout C  ]0, 1[, on a, pour n assez grand,
]0, 1[, on a, pour n assez grand, 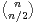
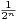 ≤ C. Donc,
≤ C. Donc,
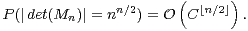
 ]0,1[,
]0,1[,
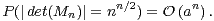
e) La question ouverte est relativement imprécise…Comme det(Mn) est centrée, l’inégalité de Bienaymé-Tchebychev donne, pour tout ε > 0,
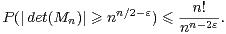
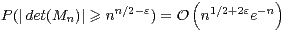
 ne dépend pas de ε.
ne dépend pas de ε.
[Liste des corrigés]

